Appendix G NAEP 2022 Sample Design

NAEP 2026 Appendix G v.36.docx

National Assessment of Educational Progress (NAEP) 2026

Appendix G NAEP 2022 Sample Design

OMB: 1850-0928

⚠️ Notice: This form may be outdated. More recent filings and information on OMB 1850-0928 can be found here:

Document [docx]

Download: docx | pdf

NATIONAL CENTER FOR EDUCATION STATISTICS

NATIONAL ASSESSMENT OF EDUCATIONAL PROGRESS

National Assessment of Educational Progress (NAEP) 2026

Appendix G

NAEP 2022 Sample Design

OMB# 1850-0928 v.36

May 2025

The 2022 Sample Design documentation is the most current version available to the public for state level NAEP assessment year. At this time, there is not a timeline for when the details for later assessment years will be publicly available.

NAEP Technical Documentation Website

NAEP Technical Documentation NAEP 2022 Sample Design

The sample design for NAEP 2022 included samples for various operational assessments. Representative samples were drawn for the following operational assessments:

long-term trend (LTT) age 9 and age 13 national assessments in mathematics and reading in public and private schools; national assessments in civics and U.S. history in public and private schools at grade 8;

national assessments in mathematics and reading in private schools at grades 4 and 8; and

state-by-state assessments and Trial Urban District Assessments (TUDA) in mathematics and reading in public schools at grades 4 and 8.

The samples for the operational assessments were organized into eight distinct groupings and sampled separately as follows: mathematics and reading assessments in public schools at grades 4 and 8;

mathematics and reading assessments in private schools at grades 4 and 8; civics and U.S. history assessments in public schools at grade 8;

civics and U.S. history assessments in private schools at grade 8;

mathematics and reading LTT assessments in public schools at age 9; mathematics and reading LTT assessments in private schools at age 9;

mathematics and reading LTT assessments in public schools at age 13; and mathematics and reading LTT assessments in private schools at age 13.

2022 State Assessment Sample Design

2022 National Grade-Based Assessment Sample Design

2022 National Long-Term Trend Assessment Sample Design

The grade 4 and grade 8 assessments were all digitally based assessments (DBA) administered using tablets. The LTT assessments were paper-based assessments (PBA) administered using paper and pencil. LTT age 9 was administered in the winter of 2022 and LTT age 13 was administered in the fall of 2022 (in a different school year than age 9).

The national assessments were designed to achieve nationally representative samples of public and private school students in the fourth or eighth grades (or public and private school students who were age 9 or 13 in the case of LTT). The target populations included all students in public, private, Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools who were enrolled in grades 4 or 8 (or who were age 9 or 13 in the case of LTT) at the time of assessment. DoDEA schools for LTT and the grade 8 civics and U.S. history assessments were limited to those located in the U.S. (not overseas).

For the fourth- and eighth-grade mathematics and reading assessments in public schools, the TUDA samples formed part of the corresponding state public school samples, and the state samples formed the public school grades 4 and 8 part of the national sample. Nationally representative samples were drawn for civics and U.S. history and for the remaining populations of private school students, DoDEA students, and BIE students separately by grade.

The state assessments were designed to achieve representative samples of students in the respective grade. At grades 4 and 8, the target populations included all students in each participating jurisdiction, which included states, District of Columbia, BIE, DoDEA, and school districts chosen for the TUDA. For each grade and assessment

subject, samples were designed to produce aggregate estimates with adequate precision for all the participating jurisdictions, as well as estimates for various student subpopulations of interest.

A one-time feature of some of the 2022 samples was maximum overlap with other earlier NAEP samples. This was done to facilitate certain analyses related to the fact that 2022 was the first assessment year after the COVID-19 pandemic. The state samples were selected to have maximum overlap with the school samples for the NAEP 2021 Monthly School Survey and the NAEP 2021 School and Teacher Questionnaire Study. The LTT samples were selected to have maximum overlap with the NAEP 2020 LTT age 9 and age 13 school samples, respectively. This overlap control was achieved for these samples by using an adaptation of the Keyfitz process.

The figure below illustrates the various sample types and subjects.

Components of the NAEP samples, by assessment subject, grade or age, and school type: 2022

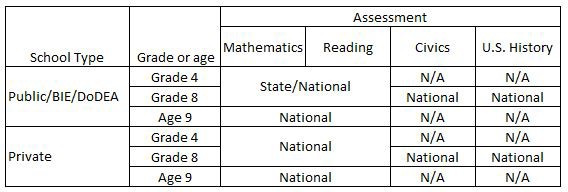
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/naep_2022_sample_design.aspx

NAEP Technical Documentation Sample Design for the 2022 National Grade-Based Assessment

The 2022 national assessment included operational assessments in mathematics and reading in public and private schools at grades 4 and 8, and operational assessments in civics and U.S. history in public and private schools at grade 8.

The sample designs aimed to achieve nationally representative samples of students in the defined populations who were enrolled at the time of assessment.

The samples were based on a two-stage sample design:

4th and 8th Grade Public School National Mathematics and Reading Assessment

4th and 8th Grade Private School National Mathematics and Reading Assessment

selection of schools within strata; and selection of students within schools.

The samples of schools were selected with probability proportional to a measure of size based on the estimated grade-specific enrollment in the schools.

For fourth- and eighth-grade public schools, the aggregate of the NAEP state student samples and assessments in mathematics and reading constitute the corresponding NAEP national student samples and assessments.

The samples for the remaining national assessments were organized into three distinct groupings and selected separately: mathematics and reading assessments in private schools at grades 4 and 8;

civics and U.S. history assessments in public schools at grade 8; and civics and U.S. history assessments in private schools at grade 8.

All of the grade 4 and grade 8 assessments were digitally based assessments (DBA) administered using tablets.

8th Grade Public School National Civics and U.S. History Assessment

8th Grade Private School National Civics and U.S. History Assessment

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sample_design_for_the_2022_national_grade_based_assessment.aspx

NAEP Technical Documentation 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The eighth-grade private school samples for the national assessments in civics and U.S. history were designed to produce nationally representative samples of students enrolled in grade eight in private schools in the United States. The target sample sizes of assessed students for the grade eight private school sample was 1,600 (800 per subject). Prior to sampling, the target sample sizes were adjusted upward to offset expected school and student attrition due to nonresponse and ineligibility.

Samples were selected using a two-stage probability-based design that involved selection of schools from within strata and selection of students within schools. The first-stage sample of schools was selected with probability proportional to a measure of size based on estimated grade-specific enrollment in the schools.

The sampling of students at the second-stage involved two steps: (1) sampling of students in the targeted grade (eighth) from each sampled school, (2) assignment of assessment subject (civics or U.S. history) to the sampled students.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

Target Population Sampling Frame Stratification of Schools School Sample Selection Substitute Schools Ineligible Schools Student Sample Selection

School and Student Participation

NAEP Technical Documentation Ineligible Schools for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The Private School Universe Survey (PSS)-based sampling frame school file, from which most of the sampled schools were drawn, corresponds to the 2019–2020 school year, two years prior to the assessment school year. During the intervening period, some of these schools either closed, no longer offered the grade of interest, or were ineligible for other reasons. In such cases, the sampled schools were coded as ineligible.

Total and Eligible Schools Sampled

Eligibility Status of Schools Sampled

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/ineligible_schools_for_the_2022_8th_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Eligibility Status of Schools Sampled for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The following table shows the unweighted counts and percentages of sampled schools that were eligible and ineligible, by reason for ineligibility, for the eighth-grade private school sample for the national assessments in civics and U.S. history.

Sampled private schools, eighth-grade national assessment, by eligibility status: 2022

Eligibility status	Unweighted count of schools	Unweighted percentage
All sampled private schools	170	100.00
Eligible	130	79.29
Ineligible	35	20.71
Has sampled grade, but no eligible students	2	1.18
Does not have sampled grade	8	4.73
Closed	7	4.14
Not a regular school	17	10.06
Duplicate on sampling frame	0	0.00
Other ineligible school	1	0.59
NOTE: Numbers of schools are rounded to nearest ten, except those pertaining to ineligible schools. Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Civics and U.S. History Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/eligibility_status_of_schools_sampled_for_the_2022_8th_grade_private_sch_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Total and Eligible Sampled Schools for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The following table presents unweighted counts and percentages of ineligible and eligible schools by private school affiliation in the eighth-grade private school sample for the national assessments in civics and U.S. history. Schools whose private school affiliation was unknown at the time of sampling subsequently had their affiliation determined during data collection. Therefore, such schools are not broken out separately and not included in the following table.

Eligibility status of sampled private schools, eighth-grade national assessment, by private school type: 2022

Private school type	Eligibility status	Unweighted count	Unweighted percentage
All private	Total	140	100.00
	Ineligible	20	14.29
	Eligible	120	85.71
Roman Catholic	Total	40	100.00
	Ineligible	0	0.22
	Eligible	40	100.00
Other private	Total	110	100.00
	Ineligible	20	18.18
	Eligible	90	81.82
NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/total_and_eligible_sampled_schools_for_the_2022_8th_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Sampling Frame for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The primary sampling frame for the 2022 eighth-grade private school sample for the national assessments in civics and U.S. history was developed from the Private School Universe Survey (PSS) corresponding to the 2019–2020 school year. The PSS file is the Department of Education’s primary database of elementary and secondary private schools in the 50 states and the District of Columbia, and it is based on a survey conducted by the U.S. Census Bureau during the 2019–2020 school year.

This sampling frame is referred to as the PSS-based sampling frame.

Nonrespondents to the PSS were also included in the primary sampling frame. Since these schools did not respond to the

Eighth-Grade Schools and Enrollment New-School Sampling Frame

PSS, their private school affiliation are unknown. Because NAEP response rates differ vastly by affiliation, to better estimate the target sample size of schools for each affiliation, additional work was done to obtain affiliation for these PSS nonrespondents. If a nonresponding school responded to a previous PSS (either two or four years prior), affiliation was obtained from the previous response. For those schools that were nonrespondents for the last two cycles of the PSS, in some cases internet research was used to establish affiliation. There were still schools with unknown affiliation remaining after this process.

A secondary sampling frame was also created for this sample to account for schools that newly opened or became newly eligible between the 2019–2020 and 2021–2022 school years. This frame contains brand-new and newly-eligible eighth-grade schools and is referred to as the new-school sampling frame. Because there are no sources available to identify new schools for non-Catholic private schools, the new-school frame for private schools contains only Catholic schools.

Both sets of sampling frames excluded schools that were ungraded, provided only special education, were part of hospital or treatment center programs, were juvenile correctional institutions, were home-school entities, or were for adult education.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_frame_for_the_2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Eighth-Grade Schools and Enrollment in the 2022 Private School Civics and U.S. History Sampling Frame

The following table presents the numbers of eighth-grade private schools and estimated enrollments, as contained in the Private School Universe Survey (PSS)-based sampling frame, by private school affiliation, for the national assessments in civics and U.S. history.

The counts presented below are of schools with known affiliation. Schools with unknown affiliation do not appear in the table because their grade span, affiliation, and enrollment were unknown. Although PSS is a school universe survey, participation is voluntary and not all private schools respond. Since the NAEP sample must represent all private schools, not just PSS respondents, a small sample of PSS nonrespondents with unknown affiliation was selected to improve NAEP coverage.

Number of schools and enrollment in eighth-grade private school sampling frame, national assessment, by affiliation: 2022

Affiliation	Number of schools	Estimated enrollment
Total	16,808	314,627
Catholic	4,426	123,133
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Civics and U.S. History Assessments.

Affiliation Number of schools Estimated enrollment

Non-Catholic

12,382

191,494

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/eighth_grade_schools_and_enrollment_in_the_2022_private_school_civics_and_us_history_sampling_frame.aspx

NAEP Technical Documentation New-School Sampling Frame for the 2022 Eighth- Grade Private School National Assessment in Civics and U.S. History

The NAEP 2022 private school frame was constructed using the most current Private School Universe Survey (PSS) file available from NCES. This file contained schools that were in existence during the 2019–2020 school year (i.e., it was two years out of date). During the subsequent 2-year period, undoubtedly, some schools closed, some changed structure (one school becoming two schools, for example), some newly opened, and still others changed their grade span.

A supplemental sample was selected from a list of Catholic schools that were new or had become newly eligible sometime after the 2019–2020 school year. The goal was to allow every new Catholic school a chance of selection, thereby fully covering the target population of Catholic schools in operation during the 2021–2022 school year. It was infeasible to ask every Catholic diocese in the United States to provide a supplemental school frame, so a two-stage procedure was employed. First, a sample of dioceses was selected. Then the National Catholic Educational Association (NCEA) was sent a list of the schools within their sampled dioceses that had been present on the 2019–2020 PSS file. NCEA was asked to add in any new schools and update grade span for the schools on this list.

The new-school process began with the preparation of a diocese-level frame. The starting point was a file containing every Catholic diocese in the United States classified as small, medium, or large based on the number of schools and student enrollment of schools from the PSS private school frame.

A diocese was considered to be small if it contained no more than one school at each targeted grade (4 and 8). During school recruitment, schools sampled from small dioceses were asked to identify schools within their dioceses that newly offered the targeted grade. Every identified new school was added to the sample. From a sampling perspective, the new school was viewed as an "annex" to the sampled school, which meant that it had a well-defined probability of selection equal to that of the sampled school. When

a school in a small diocese was sampled from the PSS frame, its associated new school was automatically sampled as well.

Dioceses that were not small were further divided into two strata, one containing large-size dioceses and a second containing medium-size dioceses. These strata were defined by computing the percentage of grade 4 and 8 enrollment represented by each diocese, sorting in descending order, and cumulating the percentages. All dioceses up to and including the first diocese at or above the 80th cumulative percentage were defined as large dioceses. The remaining dioceses were defined as medium dioceses.

A simplified example is given below. The dioceses are ordered by descending percentage enrollment. The first six become large dioceses and the last six become medium dioceses.

Example showing assignment of Catholic dioceses to the large-size and medium-size diocese strata, private school grade 8 national assessment: 2022

Diocese	Percentage enrollment	Cumulative percentage enrollment	Stratum
Diocese 1	20	20	L

Diocese Percentage enrollment Cumulative percentage enrollment Stratum

Diocese 2	20	40	L
Diocese 3	15	55	L
Diocese 4	10	65	L
Diocese 5	10	75	L
Diocese 6	10	85	L
Diocese 7	5	90	M
Diocese 8	2	92	M
Diocese 9	2	94	M
Diocese 10	2	96	M
Diocese 11	2	98	M
Diocese 12	2	100	M
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Civics and U.S. History Assessments.

In actuality, there were 77 large and 96 medium dioceses in the sampling frame.

The target sample size was 10 dioceses total across the medium and large diocese strata: eight dioceses from the large-size diocese stratum and two from the medium-size diocese stratum.

In the medium-size diocese stratum, dioceses were selected with equal probability. In the large-size diocese stratum, dioceses were sampled with probability proportional to enrollment. These probabilities were retained and used in later stages of sampling and weighting of new schools.

The following table presents the number and percentage of schools and average estimated grade enrollment for the eighth-grade new-school frame by census region. There were no new schools in the Midwest region.

Eighth-grade new school frame for the private school national assessment: number and percentage of schools and estimated enrollment by census region: 2022

Census region	Schools	Percentage	Mean school size
Total	16	100.00	35
Northeast	11	68.75	39
Midwest	0	0.00	0
South	3	18.75	15
West	2	12.50	39
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Grade 8 Civics and U.S. History Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/new_school_sampling_frame_for_the_2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation School and Student Participation in the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The tables linked to the right present weighted school and student participation rates, student exclusion rates, and student full-time remote rates for the eighth-grade private school national civics and U.S. history samples.

A weighted school participation rate indicates the percentage of the student population that is directly represented by the participating school sample.

A weighted student participation rate indicates the percentage of the student population that is directly represented by the assessed students from within participating schools.

A weighted exclusion rate indicates the percentage of students in the population that would be excluded from the assessment. Students are generally excluded from a NAEP assessment if they have a disability or limited English language proficiency that prevents them from taking the assessment altogether or the accommodations they require to take the assessment were unavailable.

A weighted full-time remote rate indicates the percentage of the student population that is full-time remote.

Weighted School Response Rates

Weighted Student Response and Exclusion Rates for the Civics Assessment

Weighted Student Response and Exclusion Rates for the

U.S. History Assessment

Weighted school participation rates are calculated by dividing the sum of school base weights, weighted by student enrollment of the targeted grade, for all participating schools by the sum of the base weights, weighted by student enrollment of the target grade, for all eligible schools. Eligible schools are all sampled schools except those considered out- of-scope. The base weight is assigned to all sampled schools and is the inverse of the probability of selection. The weighted school participation rates in these tables reflect participation prior to substitution. That is, participating substitute schools that took the place of refusing originally sampled schools are not included in the numerator.

Weighted student participation rates are calculated by dividing the sum of the student base weights for all assessed students by the sum of the student base weights for all assessable students. (See below for the response dispositions of NAEP sampled students.) Students deemed assessable are those who were assessed or absent. They do not include students that were not eligible (primarily made up of withdrawn or graduated students) or students with disabilities (SD) or English learners (EL) who were excluded from the assessment.

Weighted student exclusion rates are calculated by dividing the sum of the school nonresponse-adjusted student base weights for all excluded students by the sum for all assessable and excluded students.

Weighted student full-time remote rates are calculated by dividing the sum of the school nonresponse-adjusted student base weights for all full-time remote students by the sum for all assessable, excluded, and full-time remote students.

Every student sampled for NAEP is classified into one of the following response disposition categories: Assessed

Absent

Excluded (must be SD, EL, or SD and EL) Withdrawn or Graduated (ineligible)

Full-time remote

Assessed students were students that completed an assessment.

Absent students were students who were eligible to take an assessment but were absent from the initial session and the makeup session if one was offered. (Note, some schools, not all, had make-up sessions for students who were absent from the initial session.)

Excluded students were determined by their school to be unable to meaningfully take the NAEP assessment in their assigned subject, even with an accommodation. Excluded students must also be classified as SD and/or EL.

Withdrawn or graduated students are those who have left the school before the original assessment. These students are considered ineligible for NAEP. Full-time remote students are enrolled in brick-and-mortar schools but do not attend school in person. They are considered not assessable for NAEP.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_and_student_participation_in_the_2022_8th_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Weighted School Response Rates for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The following table presents unweighted counts of eligible sampled and participating schools and weighted school response rates, by school type, for the eighth-grade private school national civics and U.S. history samples.

A weighted school response rate indicates the percentage of the student population that is directly represented by the participating school sample. These response rates are based on the original sample of schools (excluding substitutes).

Eligible and participating school counts and weighted school response rates for eighth-grade private schools, national civics and U.S. history assessments, by school type: 2022

School type	Number of eligible sampled schools	Number of participating schools	Weighted school response rate (percent)
All private	130	50	33.59
Catholic	40	30	61.74
Non-Catholic	100	20	15.03
NOTE: Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_school_response_rates_for_the_2022_8th_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 Eighth-Grade Private School National Civics Assessment

The following table presents weighted student response, exclusion, and full-time remote rates, by school type, for eighth-grade private school students in the national civics sample. Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

A weighted student response rate indicates the percentage of the student population that is directly represented by the assessed students from within participating schools. A weighted exclusion rate indicates the percentage of students in the population that would be excluded from the assessment. The weighted student full-time remote rate indicates the percentage of the student population that is full-time remote (enrolled in brick-and-mortar schools but do not attend school in person).

Weighted student response, exclusion, and full-time remote rates for eighth-grade private schools, national civics assessment, by school type: 2022

School type	Weighted student response rate (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded	Weighted student full-time remote rates (percent)
All private	92.30	#	#	0.25
Catholic	91.89	#	#	#
Non-Catholic	93.55	#	#	0.41
# Rounds to zero.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Civics Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_8th_grade_private_school_nat_civics_assess.aspx

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 Eighth-Grade Private School National U.S. History Assessment

The following table presents weighted student response, exclusion, and full-time remote rates, by school type, for eighth-grade private school students in the national U.S. history sample. Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response, exclusion, and full-time remote rates for eighth-grade private schools, national U.S. history assessment, by school type: 2022

School type	Weighted student response rate (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded	Weighted student full-time remote rates (percent)
All private	93.57	#	#	0.48
Catholic	94.26	#	#	#
Non-Catholic	91.51	#	#	0.80
# Rounds to zero.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 U.S. History Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_8th_grade_private_school_nat_us_history_assess.aspx

NAEP Technical Documentation School Sample Selection for the 2022 Eighth- Grade Private School National Assessment in Civics and U.S. History

The sampled schools for the eighth-grade private school national assessments in civics and U.S. history came from two frames: the primary private school sample frame constructed from the Private School Universe Survey (PSS) file and the supplemental new-school sampling frame. Schools were sampled from each school frame with probability proportional to size using systematic sampling. Prior to sampling, schools in each frame were sorted by the appropriate implicit stratification variables in a serpentine order within each explicit sampling stratum. (For details on explicit and implicit strata used for these samples see the stratification page.) A school's measure of size was a complex function of the school's estimated grade enrollment. Only one hit was allowed for each school.

Schools from the PSS-based frame were sampled at a rate that would yield a national sample of 1,600 assessed students (800 each from the

Computation of Measures of Size

School Sample Sizes: Frame and New School

Catholic and non-Catholic school strata across both subjects). Catholic schools from the new-school frames were sampled at the same rate as those from the PSS-based frame.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_sample_selection_for_the_2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Computation of Measures of Size for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

In designing the eighth-grade private school civics and U.S. history assessment samples, five objectives underlie the process of determining the probability of selection for each school and the number of students to be sampled from each selected school:

to meet the target student sample size for each grade; to select an equal-probability sample of students;

to limit the number of students selected from any one school;

to ensure that the sample within a school does not include a very high percentage of the students in the school, unless all students are included; and to reduce the sampling rate of small schools, in recognition of the greater cost and burden per student of conducting assessments in such schools.

The goal in determining the school's measure of size is to optimize across the last four objectives in terms of maintaining the precision of estimates and the cost effectiveness of the sample design.

Therefore, to meet the target student sample size objective and achieve a reasonable compromise among the next other objectives, the following algorithm was used to assign a measure of size to each school based on its estimated grade enrollment as indicated on the sampling frame.

In the formula below, `x_{js}` is the estimated grade enrollment for stratum `j` and school `s`, `y_{j}` is the target within-school student sample size for stratum `j`, and

`z_{js}` is the within-school take-all student cutoff for stratum `j` to which school `s` belongs, and `P_{s}` is a primary sampling unit (PSU) weight associated with the private school universe (PSS) area sample.

For grade 8, the within-school target sample size (`y_{j}`) was 50 and take-all cutoff was 52. The preliminary measure of size (MOS) was calculated as follows:

\begin{equation} MOS_{js} =

P_{s} \times \left\{ \begin{array}{l} x_{js} & \text{if } z_{j} < x_{js} \\[2pt]

y_{j} & \text{if } 20 < x_{js} \leq{z_{j}} \\[2pt]

\left(\dfrac{y_j}{20}\right) \times x_{js} & \text{if } 5 < x_{js} \leq {20} \\

\dfrac{y_j}{4} & x_{js} \leq {5} \end{array}\right.

\end{equation}

The preliminary school measure of size was rescaled to create an expected number of hits by applying a multiplicative constant `b_{j}`, which varies by school type. It follows that the final measure of size, `E_{js}`, was defined as: \begin{equation}

E_{js}=min(b_{j}\times MOS_{js}, u_{j}),

\end{equation} where `u_{j}` is the maximum number of hits allowed. For the 2022 private schools sample, the limit was one hit.

One can choose a value of `b_{j}` such that the expected overall student sample yield matches the desired targets specified by the design, where the expected yield is calculated by summing the product of an individual school’s probability and its student sample yield across all schools in the frame.

The school's probability of selection `pi_{js}` was given by: \begin{equation}

\pi_{js}=min(E_{js},1).

\end{equation}

In addition, new and newly-eligible Catholic schools were sampled from the new-school frame. The assigned measures of size for these schools, \begin{equation} E_{js}=min(b_{j}\times MOS_{js}\times \pi_{djs}^{-1} , u_{j}),

\end{equation} used the `b_{j}` and `u_{j}` values from the main school sample for the grade and school type (i.e., the same sampling rates as for the main school sample). The variable `pi_{djs}` is the probability of selection of the diocese into the new-school diocese `d` sample.

In addition, an adjustment was made to the initial measures of size in an attempt to reduce school burden by minimizing the number of schools selected for the NAEP 2022 national civics and U.S. history assessment and the NAEP 2022 national reading and mathematics assessment in private schools. The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, minimized the overlap of schools selected for both assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/computation_of_measures_of_size_for_the_2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation School Sample Sizes: PSS-Based and New-School Sampling Frames for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The following table presents the number of schools selected for the eighth-grade private school sample by sampling frame (Private School Universe Survey [PSS]-based and new-school) and private school affiliation.

Number of schools in the total, PSS-based and new-school samples, grade 8 private national assessment, by school type: 2022

School type	Total school sample	PSS-based school sample	New-school sample
All private	170	170	#
Catholic	40	40	#
Non-Catholic private	110	110	†
Unknown affiliation	30	30	†
# Rounds to zero. † Not applicable. NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Civics and U.S. History Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sch_samp_sizes_pss_based_and_new_school_samp_frames_for_the_2022_eighth_grade_priv_sch_nat_assess_civics_hist.aspx

NAEP Technical Documentation Stratification of Schools for the 2022 Eighth- Grade Private School National Assessment in Civics and U.S. History

The purpose of school stratification is to increase the efficiency and ensure the representativeness of school samples in terms of important school-level characteristics, such as geography (e.g., census region), urbanicity, and race/ethnicity composition. NAEP school sampling utilizes two types of stratification: explicit and implicit.

Explicit stratification partitions the sampling frame into mutually exclusive groupings called strata. The systematic samples selected from these strata are independent, meaning that each sample is selected with its own unique random start. Implicit stratification involves sorting the sampling frame, as opposed to grouping the frame. For NAEP, schools are sorted in serpentine fashion by key school characteristics within sampling strata and sampled systematically using this ordering. This type of stratification ensures the representativeness of the school samples with respect to the key school characteristics.

Explicit stratification for the NAEP 2022 private school samples was by private school type: Catholic, non-Catholic, and unknown affiliation. Private school affiliation was unknown for nonrespondents to the NCES Private School Universe Survey (PSS) for the past three cycles.

The implicit stratification of the schools involved four dimensions. Within each explicit stratum, the private schools were hierarchically sorted by census region, urbanicity status, race/ethnicity status, and estimated grade enrollment. The implicit stratification in this four-fold hierarchical stratification was achieved via a "serpentine sort".

Census region was used as the first level of implicit stratification for the NAEP 2022 private school sample. For Catholic and non-Catholic schools, all four census regions were used as strata. For schools with unknown affiliation, two strata based on census region were formed by combining the Northeast and Midwest into one stratum and the South and West into another.

The urbanicity variable was equal to the original urban-centric locale if no collapsing was necessary to cover an inadequate original cell. If collapsing was necessary, the scheme was to first collapse within the four major strata (city, suburbs, town, and rural). For example, if the expected number of large city schools sampled was less than six, large city was collapsed with midsize city. If the collapsed cell was still inadequate, they were further collapsed with small city. If a major stratum cell (all three cells collapsed together) was still deficient, it was collapsed with a neighboring major stratum cell. For example, city would be collapsed with suburbs.

The last stage of stratification was a division of the geographic/urbanicity strata into race/ethnicity strata if the expected number of schools sampled was large enough (i.e., at least equal to 12). This was done by deciding first on the number of race/ethnicity strata and then dividing the geography/urbanicity stratum into that many pieces. The school frame was sorted by the percentage of students in each school who were Black, Hispanic, or American Indian/Alaska Native. The three racial/ethnic groups defining the race/ethnicity strata were those that have historically performed substantially lower on NAEP assessments than White students. The sorted list was then divided into pieces, with roughly an equal expected number of sampled schools in each piece.

Finally, schools were sorted within stratification cells by estimated grade enrollment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_of_schools_for_the_2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Student Sample Selection for the 2022 Eighth- Grade Private School National Assessment in Civics and U.S. History

The sampling of students for the private school assessments in civics and U.S. history at eighth grade involved two steps: (1) sampling of students in the targeted grade (eighth) from each sampled school, and (2) assignment of assessment subject (civics or U.S. history) to the sampled students.

Sampling Students within Sampled Schools

Within each sampled school, a sample of students was selected from a list of students in the targeted grade such that every student had an equal chance of selection. The student lists were submitted either electronically using a system known as E-filing or on paper. In E-filing for private schools, student lists are submitted one school at a time by school coordinators in Excel files. E-filing allows schools to easily submit student demographic data electronically with the student lists, easing the burden on field supervisors and school coordinators.

Schools that are unable to submit their student lists using the E-filing system provide hardcopy lists to NAEP field supervisors. In 2022, most eighth-grade private schools in the national assessment in civics and U.S. history provided hardcopy lists. About 76 percent of the participating schools submitted hardcopy lists while 24 percent of the participating schools E-filed.

In year-round multi-track schools, students in tracks scheduled to be on break on the assessment day were removed from the student lists prior to sampling. (Student base weights were adjusted to account for these students.)

The sampling process was very similar, regardless of list submission type. The sampling process was systematic (e.g., if the sampling rate was one-half, a random starting point of one or two was chosen, and every other student on the list was selected). For E-filed schools only, where demographic data was submitted for every student in the school, students were sorted by gender and race/ethnicity before the sample was selected to implicitly stratify the sample.

In schools with up to 52 students in the targeted grade, all students were selected. In schools with more than 52 students, systematic samples of 50 students were selected. Some students enrolled in the school after the sample was selected. In such cases, new enrollees were sampled at the same rate as the students on the original list.

Assigning Assessment Subject to Sampled Students

Sampled students, including new enrollees, in each participating sampled school were assigned to either the civics or U.S. history assessment at rates of 49 percent and 51 percent, respectively, using a process known as spiraling. In this process, test forms were randomly assigned to sampled students from test form sets that had, on average, a ratio of 26 civics forms to 26 U.S. history forms. Students receiving a civics form were in the civics assessment, and students receiving a U.S. history form were in the U.S. history assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_sample_selection_for_the_2022_8th_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Substitute Schools for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

Though efforts were made to secure the participation of all schools selected, it was anticipated that not all schools would choose to participate. NAEP uses school substitution to mitigate the effect of bias due to nonresponse. A nonparticipating sampled school is replaced by its substitute when the original school is considered a final refusal.

For the eighth-grade private school national sample, substitute schools were preselected for all sampled schools with known affiliation from the Private School Universe Survey (PSS)-based frame by sorting the school frame file according to the actual order used in sample selection (the implicit stratification). Sampled schools with unknown affiliation were not assigned substitutes.

Schools were disqualified as potential substitutes if they were already selected in the private school sample or assigned as a substitute for another private school (earlier in the sort ordering).

The two candidates for substitutes were then the two nearest neighbors of the originally sampled school in the frame sort order. To be eligible as a potential substitute, the neighbor needed to be a nonsampled school (for any grade), and within the same explicit sampling stratum and of the same affiliation as the originally sampled school. If both nearest neighbors were eligible to be substitutes, the one with a closer grade enrollment was chosen. If both nearest neighbors had the same grade enrollment (an uncommon occurrence), one of the two was randomly selected.

In the eighth-grade private school sample, seven substitute schools ultimately participated.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/substitute_schools_for_the_2022_8th_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Target Population for the 2022 Eighth-Grade Private School National Assessment in Civics and U.S. History

The target populations for the 2022 eighth-grade private school national assessment in civics and U.S. history were defined as all eighth-grade students who were enrolled in private schools located within the 50 states and the District of Columbia.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/target_population_for_the_2022_eighth_grade_private_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The eighth-grade public school samples for the national assessments in civics and U.S. history were designed to produce nationally representative samples of students enrolled in grade eight in public schools in the United States. The target sample sizes of assessed students for the eighth-grade public school samples was 14,400 (7,200 per subject). Prior to sampling, the target sample sizes were adjusted upward to offset expected school and student attrition due to nonresponse and ineligibility.

The sampling of students at the second-stage involved two steps: (1) sampling of students in the targeted grade (eighth) from each sampled school, and (2) assignment of assessment subject (civics or U.S. history) to the sampled students.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

Target Population Sampling Frame Stratification of Schools School Sample Selection Substitute Schools Ineligible Schools Student Sample Selection

School and Student Participation

NAEP Technical Documentation Ineligible Schools for the 2022

Eighth-Grade Public School National Assessment in Civics and U.S. History

The Common Core of Data (CCD)-based public school frame, from which most of the sampled schools were drawn, corresponds to the 2019–2020 school year, two years prior to the assessment school year. During the intervening period, some of these schools either closed, no longer offered the grade of interest, or were ineligible for other reasons. In such cases, the sampled school was coded as ineligible.

Total and Eligible Schools Sampled Eligibility Status of Schools Sampled

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/ineligible_schools_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Eligibility Status of Schools Sampled for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The following table shows the unweighted counts and percentages of sampled schools that were eligible and ineligible, by reason for ineligibility, for the eighth-grade public school sample for the national assessments in civics and U.S. history.

Sampled public schools, eighth-grade national assessment, by eligibility status: 2022

Eligibility status	Unweighted count of schools	Unweighted percentage
All sampled public schools	400	100.00
Eligible	390	96.51
Ineligible	14	3.49
Has sampled grade, but no eligible students	0	0.00
Does not have sampled grade	5	1.25
Closed	3	0.75
Not a regular school	6	1.50
Duplicate on sampling frame	0	0.00
Other ineligible	0	0.00
NOTE: Numbers of schools are rounded to nearest ten, except those pertaining to ineligible schools. Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/eligibility_status_of_schools_sampled_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_hist.aspx

NAEP Technical Documentation Total and Eligible Sampled Schools for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The following table presents unweighted counts and percentages of ineligible and eligible schools by census region in the eighth-grade public school sample for the national assessments in civics and U.S. history.

Eligibility status of sampled public schools, eighth-grade national assessment, by census region: 2022

Census region	Eligibility status	Unweighted count	Unweighted percentage
Total	Total	400	100.00
NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

Census region Eligibility status Unweighted count Unweighted percentage

	Ineligible	10	3.49
	Eligible	390	96.51
Northeast	Total	60	100.00
	Ineligible	0	5.45
	Eligible	50	94.55
Midwest	Total	70	100.00
	Ineligible	0	1.41
	Eligible	70	98.59
South	Total	170	100.00
	Ineligible	0	2.35
	Eligible	170	97.65
West	Total	110	100.00
	Ineligible	10	5.71
	Eligible	100	94.29

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/total_and_eligible_sampled_schools_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Sampling Frame for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The primary sampling frame for the 2022 eighth-grade public school samples for the civics and U.S. history assessments was developed from the Common Core of Data (CCD) file corresponding to the 2019–2020 school year. The CCD file is the Department of Education’s primary database of public elementary and secondary schools in the United States including U.S. territories. It includes all regular public, state-operated public, Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools open during the 2019–2020 school year. This eighth-grade sampling frame is referred to as the CCD-based sampling frame.

Eighth-Grade Schools and Enrollment

New-School Sampling Frame

A secondary sampling frame was also created for these samples to account for schools that newly opened or became newly eligible between the 2019–2020 and 2021–2022 school years. This frame contains brand-new and newly-eligible eighth-grade schools and is referred to as the new-school sampling frame.

Both sampling frames excluded ungraded schools, vocational schools with no enrollment, special education-only schools, prison and hospital schools, home school entities, virtual or online schools, adult and evening schools, and juvenile correctional institutions. Vocational schools with no enrollment serve students who split their time between the vocational school and their home school.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_frame_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Eighth-Grade Schools and Enrollment in the 2022 Public School Civics and U.S. History Sampling Frame

The following table presents the number of eighth-grade public schools and its estimated enrollment, as contained in the Common Core of Data (CCD)-based sampling frame, by census region, for the national assessments in civics and U.S. history.

Number of schools and estimated enrollment in CCD-based eighth-grade public school sampling frame, national assessment, by census region: 2022

Census region	Schools	Percent	Estimated enrollment	Percent
Total	29,272	100.00	3,844,110	100.00
Northeast	4,538	15.50	587,506	15.28
Midwest	7,843	26.79	789,395	20.54
South	9,594	32.78	1,526,006	39.70
West	7,297	24.93	941,203	24.48
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Civics and U.S. History Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/eighth_grade_schools_and_enrollment_in_the_2022_public_school_civics_and_us_history_sampling_frame.aspx

NAEP Technical Documentation New-School Sampling Frame for the 2022 Eighth- Grade Public School National Assessment in Civics and U.S. History

The primary sampling frame for the 2022 eighth-grade public school sample for the national assessments in civics and U.S. history was constructed using the most current Common Core of Data (CCD) file available from NCES. This file contained schools that were in existence during the 2019–2020 school year (i.e., it was two years out of date). During the subsequent 2-year period, undoubtedly some schools closed, some changed structure (one school becoming two schools, for example), some newly opened, and still others changed their grade span.

A supplemental sample was selected from a list of schools that were new or had become newly eligible sometime after the 2019–2020 school year. The goal was to allow every new school a chance of selection, thereby fully covering the target population of schools in operation during the 2021–2022 school year. It was infeasible to ask every school district in the United States to provide a supplemental school frame, so a two-stage procedure was employed. First, a sample of school districts was selected within each state. Then each State or Trial Urban District Assessment (TUDA) Coordinator was sent a list of the schools within their sampled districts that had been present on the 2019–2020 CCD file. The Coordinators were asked to add in any new schools and update grade span for the schools on this list.

The new-school process began with the preparation of a district-level frame. The starting point was a file containing every public school district in the United States. Specific districts were designated as in sample with certainty. They included the following districts:

districts in jurisdictions where all schools were selected for sample at either grade 4 or 8; state-operated districts;

districts in states with fewer than 10 districts;

charter-only districts (that is, districts containing no schools other than charter schools); and TUDA districts.

Then noncertainty districts were classified as small, medium, or large based on the number of schools and student enrollment of schools from the CCD-based public school frame.

A district was considered to be small if it contained no more than one school at each targeted grade (4 or 8). During school recruitment, the Coordinators were asked to identify schools within their district that newly offered the targeted grade. Every identified new school was added to the sample. From a sampling perspective, the new school was viewed as an “annex” to the sampled school which meant that it had a well-defined probability of selection equal to that of the sampled school. When a school in a small district was sampled from the CCD-based frame, its associated new school was automatically sampled as well.

Within each jurisdiction, districts that were neither certainty selections nor small were divided into two strata, one containing large-size districts and a second containing medium-size districts. These strata were defined by computing the percentage of jurisdiction grade 4 and 8 enrollment represented by each district, sorting in descending order, and cumulating the percentages. All districts up to and including the first district at or above the 80th cumulative percentage were defined as large districts. The remaining districts were defined as medium districts.

A simplified example is given below. The state's districts are ordered by descending percentage enrollment. The first six become large districts and the last six become medium districts.

Large-size and medium-size district strata example, by enrollment, stratum, and district, 2022

District	Percentage enrollment	Cumulative percentage enrollment	Stratum
1	20	20	L
2	20	40	L
3	15	55	L
4	10	65	L
5	10	75	L
6	10	85	L
7	5	90	M
8	2	92	M
9	2	94	M
10	2	96	M

District Percentage enrollment Cumulative percentage enrollment Stratum

11	2	98	M
12	2	100	M
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Grade 8 Civics and U.S. History Assessments.

The target sample size for each jurisdiction was 10 districts total across the medium-size and large-size district strata. Where possible, eight districts were selected from the large-size district stratum and two districts from the medium-size district stratum. However, in the example above, since there are only six large districts, all of the districts in the large district stratum and four districts from the medium district stratum would have been selected for the new-school inquiry.

If sampling was needed in the medium-size district stratum, districts in this stratum were selected with equal probability. If sampling was needed in the large-size district stratum, the districts in this stratum were sampled with probability proportional to enrollment. These probabilities were retained and used in later stages of sampling and weighting of new schools.

The following table presents the number and percentage of schools and average estimated grade enrollment for the eighth-grade new-school frame by census region.

Eighth-grade new school frame for the public school national assessment: number and percentage of schools and estimated enrollment, by census region: 2022

Census region	Schools	Percentage	Mean school size
Total	340	100.00	57
Northeast	51	15.00	104
Midwest	68	20.00	36
South	159	46.76	51
West	62	18.24	54
NOTE: Detail may not sum to totals because of rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Grade 8 Civics and U.S. History Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/new_school_sampling_frame_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation School and Student Participation in the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The tables linked to the right present weighted school and student participation rates, student exclusion rates, and student full-time remote rates for the eighth-grade public school national civics and U.S. history samples.

A weighted school participation rate indicates the percentage of the student population that is directly represented by the participating school sample.

A weighted student participation rate indicates the percentage of the student population that is directly represented by the assessed students from within participating schools.

A weighted exclusion rate indicates the percentage of students in the population that would be excluded from the assessment. Students

Weighted School Response Rates

Weighted Student Response and Exclusion Rates for Civics

Weighted Student Response and Exclusion Rates for U.S. History

are generally excluded from a NAEP assessment if they have a disability or limited English language proficiency that prevents them from taking the assessment altogether or the accommodations they require to take the assessment were unavailable.

A weighted full-time remote rate indicates the percentage of the student population that is full-time remote.

Every student sampled for NAEP is classified into one of the following response disposition categories: Assessed

Absent

Excluded (must be SD, EL, or SD and EL) Withdrawn or Graduated (ineligible)

Full-time remote

Assessed students were students that completed an assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_and_student_participation_in_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Weighted School Response Rates for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The following table presents unweighted counts of eligible sampled and participating schools and weighted school response rates, by census region, for the eighth-grade public school national civics and U.S. history samples.

Eligible and participating school counts and weighted school response rates for eighth-grade public schools, national civics and U.S. history assessments, by census region: 2022

Census region	Number of eligible sampled schools	Number of participating schools	Weighted school response rate (percent)
National	390	360	91.00
Northeast	50	50	87.13
Midwest	70	70	91.59
South	170	160	96.50
West	100	80	83.29
NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_school_response_rates_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 Eighth-Grade Public School National Civics Assessment

The following table presents weighted student response, exclusion, and full-time remote rates, by census region, for eighth-grade public school students in the national civics sample. Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response, exclusion, and full-time remote rates for eighth-grade public schools, national civics assessment, by census region: 2022

Census region	Weighted student response rates (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded	Weighted student full-time remote rates (percent)
National	89.96	1.16	0.60	1.30
Northeast	87.98	0.95	0.61	0.36
Midwest	91.13	1.04	0.49	0.77
South	90.52	1.21	0.48	1.54
West	88.98	1.31	0.90	1.97
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Civics Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_eighth_grade_public_school_nat_civics_assess.aspx

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 Eighth-Grade Public School National U.S. History Assessment

The following table presents weighted student response, exclusion, and full-time remote rates, by census region, for eighth-grade public school students in the national U.S. history sample. Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response, exclusion, and full-time remote rates for eighth-grade public schools, national U.S. history assessment, by census region: 2022

Census region	Weighted student response rates (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded	Weighted student full-time remote rates (percent)
National	89.58	1.42	0.51	1.09
Northeast	88.37	1.33	0.58	0.64
Midwest	90.85	0.98	0.40	0.86
South	89.70	1.54	0.52	1.08
West	88.87	1.68	0.56	1.63
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 U.S. History Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_8th_grade_public_school_nat_us_history_assess.aspx

NAEP Technical Documentation School Sample Selection for the 2022 Eighth- Grade Public School National Assessment in Civics and U.S. History

The sampled schools for the eighth-grade public school national assessments in civics and U.S. history came from two frames: the primary public school sample frame constructed from the Common Core of Data (CCD) and the supplemental new-school sample frame. Schools were sampled from each school frame with probability proportional to size using systematic sampling. Prior to sampling, schools in each frame were sorted by the appropriate implicit stratification variables in a serpentine order. (For details on the implicit stratification variables used for these samples see the stratification page.) A school's measure of size was a complex function of the school's estimated grade enrollment. Only one hit was allowed for each school.

Computation of Measures of Size

School Sample Sizes: CCD-Based and New School

Schools from the CCD-based frame were sampled at a rate that would yield a national sample of 14,400 assessed students across both subjects. Schools from the new-school frame were sampled at the same rate as those from the CCD-based frame.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_sample_selection_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Computation of Measures of Size for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

In designing the eighth-grade public school civics and U.S. history assessment samples, six objectives underlie the process of determining the probability of selection for each school and the number of students to be sampled from each selected school:

to meet the overall target student sample size;

to select an equal-probability sample of students from each explicit sampling stratum; to limit the number of students selected from any one school;

to ensure that the sample within a school does not include a very high percentage of the students in the school, unless all students are included;

to reduce the sampling rate of small schools, in recognition of the greater cost and burden per student of conducting assessments in such schools; and to increase the number of Black, Hispanic, and American Indian/Alaska Native (AI/AN) students in the sample.

Therefore, to meet the target student sample size objective and achieve a reasonable compromise among the next four objectives, the following algorithm was used to assign a measure of size to each school based on its estimated grade enrollment as indicated on the sampling frame.\begin{equation} MOS_{js} = \left\{\begin{array}{llll} x_{js} &

\text{if } z_{j} < x_{js} \\[2pt] y_{j} & \text{if } 20 < x_{js} \leq{z_{j}} \\ \biggl(\dfrac{y_j}{20}\biggr) \times x_{js} & \text{if } 5 < x_{js} \leq {20} \\ \dfrac{y_j}{4} & x_{js} \leq {5} \end{array}\right. \end{equation}

where $x_{js}$ is the estimated grade 8 enrollment for school $s$ in stratum $j$, and $y_{j}$ is the target within-school student sample size for stratum $j$, and `z_{js}` is the within-school take-all student cutoff for stratum `j` to which school `s` belongs.

Likewise, to increase the number of Black and Hispanic students in the sample, the measures of size for schools with relatively high proportions of Black and Hispanic students (15 percent or more and with at least 10 Black or Hispanic students in grade 8) were doubled.

This approach is effective in increasing the sample sizes of AI/AN, Black, and Hispanic students without inducing undesirably large design effects on the sample, either overall, or for particular subgroups.

For schools with high proportions of AI/AN students, the preliminary measures of size were calculated as follows: \begin{equation} MOS_{js} = 4 \times \left\{ \begin{array}

{l} x_{js} & \text{if } z_{j} < x_{js} \\[2pt] y_{j} & \text{if } 20 < x_{js} \leq{z_{j}} \\ \biggl(\dfrac{y_j}{20}\biggr) \times x_{js} & \text{if } 5 < x_{js} \leq {20} \\

\dfrac{y_j}{4} & x_{js} \leq {5} \end{array}\right. \end{equation}

For schools with high proportions of Black and Hispanic students, the preliminary measures of size were calculated as follows: \begin{equation} MOS_{js} = 2 \times \left\{

\begin{array}{l} x_{js} & \text{if } z_{j} < x_{js} \\[2pt] y_{j} & \text{if } 20 < x_{js} \leq{z_{j}} \\ \biggl(\dfrac{y_j}{20}\biggr) \times x_{js} & \text{if } 5 < x_{js} \leq

{20} \\ \dfrac{y_j}{4} & x_{js} \leq {5} \end{array}\right. \end{equation}

For all other schools (those with low proportions of AI/AN and Black and Hispanic students), the preliminary measures of size were calculated as follows: \begin{equation} MOS_{js} = \left\{\begin{array}{llll} x_{js} & \text{if } z_{j} < x_{js} \\[2pt] y_{j} & \text{if } 20 < x_{js} \leq{z_{j}} \\ \biggl(\dfrac{y_j}{20}\biggr) \times x_{js} &

\text{if } 5 < x_{js} \leq {20} \\ \dfrac{y_j}{4} & x_{js} \leq {5} \end{array}\right. \end{equation} where $x_{js}$ is the estimated grade 8 enrollment for school $s$ in stratum $j$, $y_{j}$ is the target within-school student sample size for stratum $j$, and `z_{js}` is the within-school take-all student cutoff for stratum `j` to which school `s` belongs.

For the eighth-grade public school sample, the target sample size was 50, and the take-all cutoff was 52.

The preliminary school measure of size is rescaled to create an expected number of hits by applying a multiplicative constant $b_{j}$, which varies by stratum $j$. One can choose a value of $b_{j}$ such that the expected overall student sample yield matches the desired target specified by the design, where the expected yield is calculated by summing the product of an individual school's probability and its student yield across all schools in the frame.

It follows that the final measure of size, $E_{js}$, was defined as: $$E_{js}=min(b_{j}\times MOS_{js},u_{j})$$ where $u_{j}$ is the maximum number of hits allowed. For the 2022 eighth-grade public school sample, the limit was one hit.

The school's probability of selection, `\pi_{js}`, was given by:

\begin{equation}

\pi_{js}=min(E_{js},1).

\end{equation} In addition, new and newly-eligible schools were sampled from the new-school frame. The assigned measures of size for these schools,

$$E_{js}=min(b_{j}\times MOS_{js} \times \pi_{djs}^{-1},u_{j})$$ used the $b_{j}$ and $u_{j}$ values from the CCD-based school frame for stratum $j$ (i.e., the same sampling rate as for the CCD-based school sample within each stratum). $\pi_{djs}$ is the probability of selection of the district into the new-school district ($d$) sample.

In addition, an adjustment was made to the initial measures of size in an attempt to reduce school burden by minimizing the number of schools selected for both the NAEP 2022 national assessment and the NAEP 2022 state assessments in public schools. The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, minimized the overlap of schools selected for both assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/computation_of_measures_of_size_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation School Sample Sizes: CCD-Based and New-School Sampling Frames for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The following table presents the number of schools selected for the eighth-grade public school sample by sampling frame (Common Core of Data [CCD]-based and new- school) and census region.

Public school sample counts for the eighth-grade national assessments, by census region and sampling frame (CCD-based, new-school): 2022

Census region

Total school sample

CCD-based school sample

New-school sample

Census region Total school sample CCD-based school sample New-school sample

Total	400	400	10
Northeast	60	50	#
Midwest	70	70	#
South	170	170	#
West	110	110	#
# Rounds to zero.

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Civics and U.S. History Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_samp_ccd_based_and_new_sch_samp_frames_for_the_2022_8th_gr_pub_sch_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Stratification of Schools for the 2022 Eighth- Grade Public School National Assessment in Civics and U.S. History

The purpose of school stratification is to increase the efficiency and ensure the representativeness of school samples in terms of important school-level characteristics, such as geography (e.g., census division), urbanicity, and race/ethnicity composition. NAEP school sampling utilizes two types of stratification: explicit and implicit.

Implicit stratification involves sorting the sampling frame, as opposed to grouping the frame. For NAEP, schools are sorted in serpentine fashion by key school characteristics within sampling strata and sampled systematically using this ordering. This type of stratification ensures the representativeness of the school samples with respect to the key school characteristics.

The sampling of public schools for the grade 8 assessments in civics and U.S. history did not involve any explicit stratification, but it involved six dimensions of implicit stratification. The frames were hierarchically sorted by the following in the order shown to create the implicit strata:

American Indian/Alaska Native (AI/AN) composition; Census division;

urbanicity status;

Black/Hispanic composition;

school type (public, Bureau of Indian Education (BIE), Department of Defense Education Activity (DoDEA); and median income (except for California schools where achievement data is used instead).

AI/AN Composition

For the eighth-grade civics and U.S. history assessments in the national public school sample, implied strata were created by first classifying schools on the sampling frame as either low AI/AN or high AI/AN based on the percentage of AI/AN students in the targeted grade (the cutoff was 5 percent AI/AN students). The use of AI/AN classification in this manner is part of an oversampling scheme to ensure sufficient numbers of AI/AN students are present in the student samples. Grouping high AI/AN schools together in a sampling stratum helps bring schools with relatively large numbers of AI/AN students into the school sample. In turn, schools with more AI/AN students improve the chance that sufficient numbers of AI/AN students are included in the student samples.

Census Division

Within each of the low and high AI/AN classifications, schools were further classified into groups based on census division. A census division-based grouping can consist of a single census division, a set of neighboring census divisions, or a part of an individual census division. When census divisions are combined to form implied sampling strata, it is done generally within census regions. Because there are so few high AI/AN schools, the census division grouping within the high AI/AN stratum consisted of several neighboring census divisions.

Within the low AI/AN stratum, each census division, except the Pacific Census Division, constituted a separate census division grouping. The Pacific Census Division was split into two parts: California in one part and Alaska, Hawaii, Oregon, and Washington in the other part. This was done purposely so that California could use achievement data as the last stratification variable instead of median income. See last paragraph for more detail.

Urbanicity Status

The urbanicity classification strata were derived from the NCES urban-centric locale variable from the Common Core of Data (CCD), which classifies schools based on location ([1] city, [2] suburb, [3] town, [4] rural) and proximity to urbanized areas. Urban-centric locale has 12 possible values.

The urbanicity classification cells were created by starting with the original 12 NCES urban-centric locale categories within each AI/AN classification-by-census division grouping. Any cell with an expected school sample size less than four was combined with a neighboring cell within the same census division grouping. Collapsing was first done among the subcategories within a location class. (For example, the subcategories for location class city are (1) large, (2) mid-size, and (3) small. If one of these subcategories was deficient then either 1 was collapsed with 2; 3 collapsed with 2; or 2 collapsed with the smaller of 1 or 3.) If the collapsed cell was still too small, all three subcategories within a location class were combined.

If a collapsed location class still had an expected school sample size less than four, then it was collapsed with a neighboring collapsed location class. That is, location class 1 would be collapsed with 2, or location class 3 would be collapsed with 4. If additional collapsing was necessary, all location classes were combined. No collapsing across census division strata was allowed or necessary.

The result of this was a set of sampling strata defined by AI/AN classification, census division strata, and urbanicity classification having expected school sample sizes of at least four schools.

No further implicit strata for High AI/AN schools were formed beyond urbanization classification.

Black/Hispanic Composition

Low AI/AN schools within the nested urbanicity classification strata were further stratified into Black/Hispanic classification strata. The first division was the classification of schools as either low Black/Hispanic schools or high Black/Hispanic schools based on the total percentage of Black and Hispanic students in the target grade (the cutoff was 15 percent total Black and Hispanic students). Within the high Black/Hispanic classification, the number of substrata was based on the expected school sample size.

If the expected school sample size of resultant stratum was less than or equal to 8.0, then this was the final urbanicity-Black/Hispanic stratum;

if the expected sample size was greater than or equal to 8.0 and less than 12.0, there were two substrata;

if the expected sample size was greater than or equal to 12.0 and less than 16.0, there were three substrata; and if the expected sample size was greater than or equal to 16.0, there were four substrata.

The substrata were defined by total percentage of Black and Hispanic students, with the cutoffs for substrata defined by weighted percentiles (with the weight equal to expected hits for each school).

For two substrata, the cutoff was the weighted median;

for three substrata, the weighted 33rd and 67th percentiles; and for four substrata, the weighted median and quartiles.

For the low Black/Hispanic classification, there were six urbanicity strata that had a large enough expected school sample size, and these were split into groups of states. Two or three state groups were formed using adjacent states if possible, while maintaining an expected school sample size of at least four for each state group for each of these six urbanicity strata.

School Type

The next implicit stratification variable was school type. School type takes on values of public, BIE, and DoDEA.

Median Income/Achievement

The last implicit stratification variable was median income of the ZIP code area containing the school, except in California, where student achievement data was used. Schools in California contain more than 12 percent of the grade 8 students in the nation. Using achievement data provides a benefit. Achievement is a better sort variable than median income when ordering schools within a state because it is direct measure of student performance. However, when ordering schools across states, median income is better than achievement because states generally use different achievement measures while median income is a standard measure across states.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_of_schools_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Student Sample Selection for the 2022 Eighth- Grade Public School National Assessment in Civics and U.S. History

The sampling of students for the public school assessments in civics and U.S. history at eighth grade involved two steps: (1) sampling of students in the targeted grade (eighth) from each sampled school, and (2) assignment of assessment subject (civics or U.S. history) to the sampled students.

Sampling Students within Sampled Schools

jurisdiction at once (known as multiple school E-file submission). E-filing allows schools to easily submit student demographic data electronically with the student lists, easing the burden on field supervisors and school coordinators.

Schools that are unable to submit their student lists using the E-filing system provide hardcopy lists to NAEP field supervisors. In 2022, approximately 99 percent of the participating eighth-grade public schools in the national assessment in civics and U.S. history E-filed their student lists while approximately 1 percent of the participating schools submitted hardcopy lists.

Assigning Assessment Subject to Sampled Students

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_sample_selection_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Substitute Schools for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

For the eighth-grade public school national sample, substitute schools were preselected for all sampled schools from the Common Core of Data (CCD)-based sampling frame by sorting the school frame file according to a sort order very close to that used in sample selection (the implicit stratification). The two exceptions to this were as follows: (1) estimated grade enrollment replaces median income (achievement) as the last sort variable, and (2) school type in the stratification hierarchy was crossed with state (rather than used alone). The first change guaranteed that the selected substitute would have a grade enrollment very close to that of the originally selected school. The second change guaranteed that any selected substitutes would be within the same state as the originally sampled nonresponding school.

Schools were disqualified as potential substitutes if they were already selected in the public school sample or assigned as a substitute for another public school (earlier in the sort ordering).

The two candidates for substitutes were then the two nearest neighbors of the originally sampled school in this revised sort order. To be eligible as a potential substitute, the neighbor needed to be a nonsampled school (for any grade) and within the same explicit sampling stratum. If both nearest neighbors were eligible to be substitutes, the one with a closer grade enrollment was chosen. If both nearest neighbors had the same grade enrollment (an uncommon occurrence), one of the two was randomly selected.

In the eighth-grade public school sample, seven substitute schools ultimately participated.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/substitute_schools_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation Target Population for the 2022 Eighth-Grade Public School National Assessment in Civics and U.S. History

The target population for the 2022 eighth-grade public school national assessments in civics and U.S. history was defined as all eighth-grade students who were enrolled in public schools, Bureau of Indian Education (BIE) schools, and Department of Defense Education Activity (DoDEA) schools located within the 50 states and the District of Columbia.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/target_population_for_the_2022_eighth_grade_public_school_nat_assess_in_civics_and_us_history.aspx

NAEP Technical Documentation 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The fourth- and eighth-grade private school samples for the national mathematics and reading assessments were designed to produce nationally representative samples of students enrolled in fourth and eighth grade in private schools in the United States.

The target sample sizes of assessed students for each grade and subject are shown in the table below. Prior to sampling, these target sample sizes were adjusted upward to offset expected school and student attrition due to nonresponse and ineligibility.

Samples were selected using a two-stage probability design that involved selection of schools within strata and selection of students within schools. The first-stage samples of schools were selected with probability proportional to a measure of size based on the estimated grade-specific enrollment in the schools.

Target Population Sampling Frame Stratification of Schools School Sample Selection Substitute Schools

The sampling of students at the second-stage involved two steps: (1) sampling of students in the targeted grade (fourth or eighth) from each sampled school, and (2) assignment of assessment subject (mathematics or reading) to the sampled students.

Target sample sizes of assessed students, private school national assessment, by subject and grade: 2022

Ineligible Schools Student Sample Selection

School and Student Participation

Grade	Total	Mathematics	Reading
Total	9,400	4,700	4,700
4	4,700	2,350	2,350
8	4,700	2,350	2,350
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Mathematics and Reading Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/2022_fourth_and_eighth_grade_private_school_national_assessment_in_mathematics_and_reading.aspx

NAEP Technical Documentation Ineligible Schools for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The Private School Universe Survey (PSS)-based private school frames, from which most of the sampled schools were drawn, correspond to the 2019–2020 school year, two years prior to the assessment school year. During the intervening period, some of these schools either closed, no longer offered the grade of interest, or were ineligible for other reasons. In such cases, the sampled schools were coded as ineligible.

Total and Eligible Schools Sampled

Eligibility Status of Schools Sampled

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/ineligible_schools_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Eligibility Status of Schools Sampled for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The following table shows the unweighted counts and percentages of sampled schools that were eligible and ineligible, by reason for ineligibility, for the fourth- and eighth- grade private school national mathematics and reading samples.

Sampled private schools, national assessment, by grade and eligibility status: 2022

Grade and eligibility status	Unweighted count of schools	Unweighted percentage
All fourth-grade sampled private schools	390	100.00
Eligible	340	86.29
Ineligible	54	13.71
Has sampled grade, but no eligible students	5	1.27
Does not have sampled grade	8	2.03
Closed	19	4.82
Not a regular school	19	4.82
Duplicate on sampling frame	2	0.51
Other ineligible school	1	0.25
All eighth-grade sampled private schools	380	100.00
Eligible	330	86.95
Ineligible	50	13.05
Has sampled grade, but no eligible students	4	1.04
Does not have sampled grade	7	1.83
Closed	19	4.96
Not a regular school	20	5.22
Duplicate on sampling frame	0	0.00
Other ineligible school	0	0.00
NOTE: Numbers of schools are rounded to nearest ten, except those pertaining to ineligible schools. Detail may not sum to totals due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/eligibility_status_of_schools_sampled_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Total and Eligible Sampled Schools for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The following table presents unweighted counts and percentages of ineligible and eligible schools by private school affiliation in the fourth- and eighth-grade private school national mathematics and reading samples. Schools whose private school affiliation was unknown at the time of sampling subsequently had their affiliation determined during

data collection. Therefore, such schools are not broken out separately and not included in the following table.

Eligibility status of sampled private schools, national assessment, by grade and private school type: 2022

Fourth grade				Eighth grade
Private school type	Eligibility status	Unweighted count	Unweighted percentage	Unweighted count	Unweighted percentage
All private	Total	370	100.00	360	100.00
	Ineligible	40	11.11	30	9.22
	Eligible	330	88.89	330	90.78
Catholic	Total	120	100.00	110	100.00
	Ineligible	10	5.08	10	5.56
	Eligible	110	94.92	100	94.44
Non-Catholic	Total	250	100.00	250	100.00
	Ineligible	40	13.94	30	10.80
	Eligible	220	86.06	220	89.20
NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/total_and_eligible_sample_schools_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Sampling Frame for the 2022 Fourth- and Eighth- Grade Private School National Assessment in Mathematics and Reading

The primary sampling frames for the 2022 fourth- and eighth-grade private school samples for the national mathematics and reading assessments were developed from the Private School Universe Survey (PSS) corresponding to the 2019–2020 school year. The PSS file is the Department of Education’s primary database of elementary and secondary private schools in the 50 states and the District of Columbia, and it is based on a survey conducted by the U.S. Census Bureau during the 2019–2020 school year. These sampling frames are referred to as the PSS-based sampling frames.

Nonrespondents to the PSS were also included in the primary sampling frames. Since these schools did not respond to the

Fourth- and Eighth-Grade Schools and Enrollment

New-School Sampling Frame

PSS, their private school affiliation are unknown. Because NAEP response rates differ vastly by affiliation, to better estimate the target sample size of schools for each affiliation, additional work was done to obtain affiliation for these PSS nonrespondents. If a nonresponding school responded to a previous PSS (either two or four years prior), affiliation was obtained from the previous response. For those schools that were nonrespondents for the last three cycles of the PSS, in some cases internet research was used to establish affiliation. There were still schools with unknown affiliation remaining after this process.

A secondary set of sampling frames were also created for these samples to account for schools that newly opened or became newly eligible between the 2019–2020 and 2021– 2022 school years. These frames contain brand-new and newly-eligible fourth- and eighth-grade schools and are referred to as the new-school sampling frames. Because there are no sources available to identify new schools for non-Catholic private schools, the new school frame for private schools contains only Catholic schools.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_frame_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Fourth- and Eighth-Grade Schools and Enrollment in the 2022 Private School Mathematics and Reading Sampling Frame

The following table presents the number of fourth- and eighth-grade private schools and their estimated enrollment as contained in the Private School Universe Survey (PSS)- based sampling frames, by private school affiliation, for the national mathematics and reading assessments. Grade-specific enrollment was estimated for each school as the average grade enrollment for grades 1 through 8.

The counts in this table are for schools with known affiliation. Schools with unknown affiliation do not appear in the table because their grade span, affiliation, and enrollment were unknown. Although PSS is a school universe survey, participation is voluntary and not all private schools respond. Since the NAEP sample must represent all private schools, not just PSS respondents, a small sample of PSS nonrespondents with unknown affiliation was selected for each of the targeted grades to improve NAEP coverage.

Number of schools and enrollment in private school sampling frame, national assessment, by grade and affiliation: 2022

Grade	Affiliation	Number of schools	Estimated enrollment
4	Total	18,352	320,372
	Catholic	4,808	122,653
	Non-Catholic	13,544	197,719
8	Total	16,894	317,439
	Catholic	4,451	124,017
	Non-Catholic	12,443	193,422
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Mathematics and Reading Assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/fourth_and_eighth_grade_schools_and_enrollment_in_the_2022_private_school_sampling_frame.aspx

NAEP Technical Documentation New-School Sampling Frame for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The new-school process began with the preparation of a diocese-level frame. The starting point was a file containing every Catholic diocese in the U.S. classified as small, medium, or large based on the number of schools and student enrollment of schools from the PSS private school frame.

A diocese was considered to be small if it contained no more than one school at each targeted grade (4 or 8). During school recruitment, schools sampled from small dioceses were asked to identify schools within their dioceses that newly offered the targeted grade. Every identified new school was added to the sample. From a sampling perspective, the new school was viewed as an "annex" to the sampled school, which meant that it had a well-defined probability of selection equal to that of the sampled school. When

a school in a small diocese was sampled from the PSS frame, its associated new school was automatically sampled as well.

and including the first diocese at or above the 80th cumulative percentage were defined as large dioceses. The remaining dioceses were defined as medium dioceses.

A simplified example is given below. The dioceses are ordered by descending percentage enrollment. The first six become large dioceses and the last six become medium dioceses.

Example showing assignment of Catholic dioceses to the large-size and medium-size diocese strata, private school national mathematics and reading assessments: 2022

Diocese	Percentage enrollment	Cumulative percentage enrollment	Stratum
Diocese 1	20	20	L
Diocese 2	20	40	L
Diocese 3	15	55	L
Diocese 4	10	65	L
Diocese 5	10	75	L
Diocese 6	10	85	L
Diocese 7	5	90	M

Diocese Percentage enrollment Cumulative percentage enrollment Stratum

Diocese 8	2	92	M
Diocese 9	2	94	M
Diocese 10	2	96	M
Diocese 11	2	98	M
Diocese 12	2	100	M
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Mathematics and Reading Assessments.

In actuality, there were 77 large and 96 medium dioceses in the sampling frame.

The target sample size was 10 dioceses total across the medium-size and large-size diocese strata: eight from the large-size diocese stratum and two from the medium-size diocese stratum.

The following table presents the number and percentage of schools and average estimated grade enrollment for the fourth- and eighth-grade "new-school" frame by census region. There were no new schools in Midwest region.

Number and percentage of schools and mean school size in the new-school frame, national private assessment, by grade and census region: 2022

Census region	Grade 4			Grade 8
Census region	Schools	Percentage	Mean school size	Schools	Percentage	Mean school size
Total	14	100.00	35	16	100.00	35
Northeast	10	71.43	41	11	68.75	39
Midwest	0	0.00	0	0	0.00	0
South	3	21.43	15	3	18.75	15
West	1	7.14	35	2	12.50	39
NOTE: Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/new_school_sampling_frame_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation School and Student Participation in the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The tables linked to the right present weighted school and student participation rates, student exclusion rates, and student full-time remote rates for the fourth- and eighth-grade private school national mathematics and reading samples.

A weighted school participation rate indicates the percentage of the student population that is directly represented by the participating school sample.

A weighted student participation rate indicates the percentage of the student population that is directly represented by the assessed students from within participating schools.

A weighted full-time remote rate indicates the percentage of the student population that is full-time remote.

Weighted School Response Rates

Weighted Student Response and Exclusion Rates for Mathematics

Weighted Student Response and Exclusion Rates for Reading

Every student sampled for NAEP is classified into one of the following response disposition categories: Assessed

Absent

Excluded (must be SD, EL, or SD and EL)

Withdrawn or Graduated (ineligible) Full-time remote

Assessed students were students that completed an assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_and_student_participation_in_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Weighted School Response Rates for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The following table presents unweighted counts of eligible sampled and participating schools and weighted school response rates, by school type, for the fourth- and eighth- grade private school national mathematics and reading samples.

Eligible and participating school counts and weighted school response rates for fourth- and eighth-grade private schools, national mathematics and reading assessments, by school type: 2022

Grade

Private school type

Number of eligible sampled schools

Number of participating schools

Weighted school response rate (percent)

All private

340

150

37.50

NOTE: Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

Grade Private school type Number of eligible sampled schools Number of participating schools Weighted school response rate (percent)

Catholic	110	90	66.61
Non-Catholic	230	60	20.01
8 All private	330	130	35.49
Catholic	100	80	60.98
Non-Catholic	230	60	19.80

NOTE: Detail may not sum to total due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_school_response_rates_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 Fourth- and Eighth-Grade Private School National Mathematics Assessment

The following table presents weighted student response, exclusion, and full-time remote rates, by school type, for the fourth- and eighth-grade private school national mathematics samples. Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response, exclusion, and full-time remote rates for private schools, national mathematics assessment, by grade and school type: 2022

Weighted student			Weighted percentage of	Weighted percentage of	Weighted student
Grade	Private school type	response rate (percent)	all students who were SD and excluded	all students who were EL and excluded	full-time remote rates (percent)
4	All private	93.71	0.40	0.08	0.29
	Catholic	93.67	0.15	0.21	0.25
	Non-Catholic Private	93.77	0.54	#	0.31
8	All private	93.97	#	#	0.63
# Rounds to zero.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Mathematics Assessment.

Grade Private school type

Weighted student response rate

(percent)

Weighted percentage of all students who were SD and

excluded

Weighted percentage of all students who were EL and

excluded

Weighted student full-time remote rates

(percent)

Catholic	94.09	#	#	0.28
Non-Catholic Private	93.74	#	#	0.85

# Rounds to zero.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Mathematics Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_private_school_national_mathematics_assessment.aspx

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 Fourth- and Eighth-Grade Private School National Reading Assessment

The following table presents weighted student response, exclusion, and full-time remote rates, by school type, for the fourth- and eighth-grade private school national reading samples. Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response, exclusion, and full-time remote rates for private schools, national reading assessment, by gradae and school type: 2022

Weighted student			Weighted percentage of	Weighted percentage of	Weighted student
Grade	Private school type	response rate (percent)	all students who were SD and excluded	all students who were EL and excluded	full-time remote rates (percent)
4	All private	94.12	0.17	0.09	0.37
	Catholic	95.19	0.16	0.23	0.41
	Non-Catholic Private	92.19	0.17	#	0.34
8	All private	94.86	0.14	#	0.26
	Catholic	95.42	#	#	#
# Rounds to zero.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Reading Assessment.

Grade Private school type

Weighted student response rate

(percent)

Weighted percentage of all students who were SD and

excluded

Weighted percentage of all students who were EL and

excluded

Weighted student full-time remote rates

(percent)

Non-Catholic Private

93.72

0.22

0.43

# Rounds to zero.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Reading Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_private_school_national_reading_assessment.aspx

NAEP Technical Documentation School Sample Selection for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The sampled schools for the fourth- and eighth-grade private school national assessments in mathematics and reading came from two frames: the primary private school sample frame constructed from the Private School Universe Survey (PSS) file and the supplemental new- school sample frame. Schools were sampled from each school frame with probability proportional-to-size (PPS) using systematic sampling. Prior to sampling, schools in each frame were sorted by the appropriate implicit stratification variables in a serpentine order within each explicit sampling stratum. (For details on explicit and implicit strata used for these samples see the stratification page.) A school's measure of size was a complex function of the school's estimated grade enrollment. Only one hit was allowed for each school.

Computation of Measures of Size

School Sample Sizes: Frame and New School

Schools from the PSS-based frame were sampled at a rate that would yield a national sample of 4,700 assessed students (2,350 each from the Catholic and non-Catholic school strata) at grade 4 and at grade 8. Catholic schools from the new-school frames were sampled at the same rate as those from the PSS-based frames.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_sample_selection_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Computation of Measures of Size for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

There were five objectives underlying the process for determining the probability of selection for each school and for setting the number of students to be sampled within each selected school:

to meet the target student sample size for each grade; to select an equal-probability sample of students;

to limit the number of students selected from any one school;

The goal in determining the school's measure of size is to optimize across the last four objectives in terms of maintaining the precision of estimates and the cost effectiveness of the sample design.

Therefore, to meet the target student sample size objective and achieve a reasonable compromise among the other four objectives, the following algorithm was used to assign a measure of size to each school based on its estimated grade enrollment as indicated on the sampling frame.

In the formula below, `x_{js}` is the estimated grade enrollment for stratum `j` and school `s`, `y_{j}` is the target within-school student sample size for stratum `j,` `z_{js}` is the within-school take-all student cutoff for stratum `j` to which school `s` belongs, and `P_{s}` is a primary sampling unit (PSU) weight associated with the private school universe (PSS) area sample.

For grades 4 and 8, the target within school sample size (`y_{j}`) was 50, and the take-all cut (`z_{js}`) was 52.

For the fourth- and eighth-grade national assessment in mathematics and reading for private schools, the preliminary measures of size (MOS) were calculated as follows:

\begin{equation}

MOS_{js} = P_{s}\times \left\{ \begin{array}{l} x_{js} & \text{if } z_{js} < x_{js} \\[2pt]

y_{j} & \text{if } 20 < x_{js} \leq{z_{js}} \\[2pt]

\left(\dfrac{y_j}{20}\right) \times x_{js} & \text{if } 5 < x_{js} \leq {20} \\

\dfrac{y_j}{4} & x_{js} \leq {5} \end{array}\right.

\end{equation}

The preliminary school measure of size is rescaled to create an expected number of hits by applying a multiplicative constant `b_{j}`, which varies by grade and school type. It follows that the final measure of size, `E_{js}`, was defined as:

\begin{equation}

E_{js}=min(b_{j}\times MOS_{js}, u_{j}),

\end{equation}

where `u_{j}` is the maximum number of hits allowed. For the fourth- and eighth-grade private school samples for the mathematics and reading assessments, the limit was one hit.

The school's probability of selection, `\pi_{js}`, was given by: \begin{equation}

\pi_{js}=min(E_{js},1).

\end{equation}

In addition, new and newly-eligible Catholic schools were sampled from the new-school frame. The assigned measures of size for these schools,

\begin{equation}

E_{js}=min(b_{j}\times MOS_{js}\times\pi_{djs}^{-1} , u_{j}),

\end{equation}

used the `b_{j}` and `u_{j}` values from the main school sample for the grade and school type (i.e., the same sampling rates as for the main school sample). The variable

`\pi_{djs}` is the probability of selection of the diocese into the new-school diocese (`d`) sample.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/computation_of_measures_of_size_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation School Sample Sizes: PSS-Based and New-School for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The following table presents the number of schools selected for the fourth- and eighth-grade private school mathematics and reading samples by sampling frame (Private School Universe Survey [PSS]-based and new-school) and private school affiliation.

Number of schools in the total, PSS-based, and new-school samples, national private assessment, by grade and school type: 2022

Grade and private school type	Total school sample	PSS-based school sample	New-school sample
Grade 4
All private	390	390	#
Catholic	120	120	#
Non-Catholic	250	250	†
Unknown affiliation	30	30	†
Grade 8
All private	380	380	#
Catholic	110	110	#
Non-Catholic	250	250	†
# Rounds to zero. † Not applicable. NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 National Mathematics and Reading Assessments.

Grade and private school type Total school sample PSS-based school sample New-school sample

Unknown affiliation

†

# Rounds to zero.

† Not applicable.

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_sample_sizes_list_frame_based_and_new_school_for_the_2022_private_school_national_assessment.aspx

NAEP Technical Documentation Stratification of Schools for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

Explicit stratification for the NAEP 2022 private school samples for mathematics and reading at grades 4 and 8 was by private school type: Catholic, non-Catholic, and unknown affiliation. Private school affiliation was unknown for schools that were nonrespondents to the NCES Private School Universe Survey (PSS) for the past three cycles.

The implicit stratification of the schools involved four dimensions. Within each explicit stratum, the private schools were hierarchically sorted by census region, urbanicity classification, race/ethnicity classification, and estimated grade enrollment. The implicit stratification in this four-fold hierarchical stratification was achieved via a "serpentine sort."

Census region was used as the first level of implicit stratification for the NAEP 2022 private school sample for mathematics and reading. All four census regions were used as strata.

The next level of stratification was an urbanicity classification based on urban-centric locale, as specified on the PSS. Within a census region-based stratum, urban-centric locale cells that were too small were collapsed. The criterion for adequacy was that the cell had to have an expected school sample size of at least six. The urbanicity variable was equal to the original urban-centric locale if no collapsing was necessary to cover an inadequate original cell. If collapsing was necessary, the scheme was to first collapse within the four major strata (city, suburbs, town, and rural). For example, if the expected number of large city schools sampled was less than six, large city was collapsed with midsize city. If the collapsed cell was still inadequate, they were further collapsed with small city. If a major stratum cell (all three cells collapsed together) was still deficient, it was collapsed with a neighboring major stratum cell. For example, city would be collapsed with suburbs.

The last stage of stratification was a division of the geographic/urbanicity strata into race/ethnicity strata if the expected number of schools sampled was large enough (i.e., at

least equal to 12). This was done by deciding first on the number of race/ethnicity strata and then dividing the geography/urbanicity stratum into that many pieces. The school frame was sorted by the percentage of students in each school who were Black, Hispanic, or American Indian/Alaska Native. The three racial/ethnic groups defining the race/ethnicity strata were those that have historically performed substantially lower on NAEP assessments than White students. The sorted list was then divided into pieces, with roughly an equal expected number of sampled schools in each piece.

Finally, schools were sorted within stratification cells by estimated grade enrollment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_of_schools_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Student Sample Selection for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The sampling of students for the fourth- and eighth-grade private school national assessments in mathematics and reading involved two steps: (1) sampling of students in the targeted grade (fourth or eighth) from each sampled school, and (2) assignment of assessment subject (mathematics or reading) to the sampled students.

Sampling Students within Sampled Schools

Schools that are unable to submit their student lists using the E-filing system provide hardcopy lists to NAEP field supervisors. In 2022, most private schools in the national assessments in mathematics and reading submitted hardcopy lists rather than electronic lists. At fourth grade, 72 percent of the participating schools submitted hardcopy lists and 28 percent submitted electronic lists. At eighth grade, 70 percent of the schools submitted hardcopy lists, and 30 percent submitted electronic lists.

The sampling process was very similar, regardless of list submission type. The sampling process was systematic (e.g., if the sampling rate was one-half, a random starting point of one or two was chosen, and every other student on the list was selected). For E-filed schools only, where demographic data was submitted for every student on the frame, students were sorted by gender and race/ethnicity before the sample was selected to implicitly stratify the sample.

Assigning Assessment Subject to Sampled Students

Sampled students, including new enrollees, in each participating sampled school were assigned to either the mathematics or the reading assessment at rates of 52 percent and 48 percent, respectively for grade 4, or 50 percent for each subject for grade 8, using a process known as spiraling. In this process, test forms were randomly assigned to sampled students from test form sets that had, on average, a ratio of 26 mathematics forms to 24 reading forms for grade 4, and a ratio of 25 mathematics forms to 25 reading forms for grade 8. Students receiving a mathematics form were in the mathematics assessment, and students receiving a reading form were in the reading assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_sample_selection_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Substitute Schools for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

For the fourth- and eighth-grade private school mathematics and reading samples, substitute schools were preselected for all sampled schools with known affiliation from the Private School Universe Survey (PSS)-based sampling frames by sorting the school frame files according to the actual order used in sample selection (the implicit stratification). Sampled schools with unknown affiliation were not assigned substitutes.

Schools were disqualified as potential substitutes if they were already selected in the private school sample or assigned as a substitute for another private school (earlier in the sort ordering).

In the fourth-grade private school mathematics and reading sample, 16 substitute schools ultimately participated. In the eighth-grade private school sample, 14 substitute schools participated.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/substitute_schools_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation Target Population for the 2022 Fourth- and Eighth-Grade Private School National Assessment in Mathematics and Reading

The target populations for the 2022 fourth- and eighth-grade private school national assessments in mathematics and reading were defined as all fourth- and eighth-grade students who were enrolled in private schools located within the 50 states and the District of Columbia.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/target_population_for_the_2022_fourth_and_eighth_grade_private_school_national_assessment.aspx

NAEP Technical Documentation 2022 Fourth- and Eighth-Grade Public School National Assessment in Mathematics and Reading

For the mathematics and reading assessments in fourth- and eighth-grade public schools, the national samples were formed by the collective state assessment samples for each jurisdiction, including Bureau of Indian Education (BIE) and Department of Defense Educational Activity (DoDEA) schools. All jurisdictions participated in the mathematics and reading assessments, with the exception of Puerto Rico, where only the operational mathematics assessment was conducted.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/2022_fourth_and_eighth_grade_public_school_national_assessment_in_mathematics_and_reading.aspx

NAEP Technical Documentation Sample Design for the 2022 National Long-Term Trend Assessment

Unlike most NAEP assessments, the 2022 long-term trend (LTT) assessments target students based on age rather than grade. The age populations for NAEP 2022 are as follows:

age 9 population: all students born in 2012 (i.e., all students who were nine years old on December 31, 2021); and age 13 population: all students born in 2009 (i.e., all students who were thirteen years old on December 31, 2022).

The NAEP 2022 sample design consisted of nationally representative samples of students for the following assessments: reading at age 9;

Selection of Primary Sampling Units

2022 Public School Long-Term Trend Assessment 2022 Private School Long-Term Trend Assessment School and Student Participation Results

mathematics at age 9; reading at age 13; and mathematics at age 13.

This was accomplished by designing separate sample components for public and private schools for each age. The selected samples were based on a three-stage sample design: selection of primary sampling units (PSUs);

selection of schools within strata; and selection of students within schools.

The samples of schools were selected with probability proportional to a measure of size based on the estimated age 9 or age 13 enrollment in the schools. An adjustment was made to the initial measures of size in an attempt to ensure the inclusion of all eligible schools that were part of the 2020 LTT sample for the respective age (9 or 13). The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, maximized the overlap of schools selected for both the 2020 and 2022 LTT assessments.

The target population included all nine year old students or thirteen year old students (according to the age definitions above) in public and private schools, including Bureau of Indian Education (BIE) and Department of Defense Education Activity (DoDEA) schools located in the U.S. (but not overseas).

All LTT assessments in 2022 were paper-based assessments (PBA) administered using paper and pencil. The sample design for the long-term trend assessments is described in more detail in subsequent pages.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sample_design_for_the_2022_national_long_term_trend_assessment.aspx

Shape58

NAEP Technical Documentation 2022 Private School Long-Term Trend Assessment

The NAEP 2022 sample design yielded nationally representative samples of private school students at ages 9 and 13 for long-term trend (LTT) through a three-stage approach:

selection of primary sampling units (PSUs); selection of schools within strata; and

selection of students within schools.

The sample of schools was selected with probability proportional to a measure of size based on the estimated age enrollment in the schools.

The 2022 sampling plan was designed to assess 1,640 students in private schools for LTT at each age. These students were allocated among tests in mathematics and reading. Target sample sizes were adjusted to reflect expected private school and student response and eligibility.

Schools on the sampling frame were explicitly stratified prior to sampling by private school affiliation (Catholic, non-Catholic, and unknown affiliation). Within affiliation type, schools were implicitly stratified by PSU type (certainty/noncertainty). In certainty PSUs, further stratification was by census region, urbanization classification, and estimated age enrollment. In noncertainty PSUs, additional stratification was by PSU stratum, urbanization classification, and estimated age enrollment.

Target Population Sampling Frame Stratification of Schools Sampling of Schools Substitute Schools Ineligible Schools Student Sample Selection

From the stratified frame of private schools, systematic random samples of age-eligible schools were drawn with probability proportional to a

measure of size based on the estimated age enrollment of the school for the relevant age. The measures of size included an adjustment made in an attempt to ensure the inclusion of all eligible schools that were part of the 2020 private school long-term trend sample for ages 9 and 13. The NAEP sampling procedures used an adaptation of

the Keyfitz process to compute conditional measures of size that, by design, maximized the overlap of schools selected for both the 2020 and 2022 long-term trend assessments at each age.

Each selected school in the private school sample provided a list of eligible enrolled students from which a systematic, equal probability sample of students was drawn.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/2022_private_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Ineligible Private Schools for the 2022 Long- Term Trend Assessment

The Private School Universe Survey (PSS) school file from which most of the sampled schools were drawn corresponds to the 2019–2020 school year, two years prior to the assessment school year. During the intervening period, some of these schools either closed, no longer offered grades for the age group of interest, or were ineligible for other reasons. In such cases, the sampled schools were coded as ineligible.

The table below presents unweighted counts of sampled private schools by eligibility status, including the reason for ineligibility.

Number of sampled public schools, long-term trend assessment, by eligibility status within age: 2022

Eligibility Status	Unweighted count of schools	Unweighted percentage
All age 9 sampled public schools	160	100.00
Eligible schools	140	82.93
No age-eligible students	11	6.71
School closed	11	6.71
Not a regular school	4	2.44
Other ineligible school	0	0.00
Duplicate on sampling frame	2	1.22
All age 13 sampled public schools	180	100.00
Eligible schools	140	75.96
No age-eligible students	25	13.66
School closed	8	4.37
NOTE: Total and eligible school counts are rounded to nearest ten. Percentages are based on unrounded counts. Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Eligibility Status Unweighted count of schools Unweighted percentage

Not a regular school	10	5.46
Other ineligible school	0	0.00
Duplicate on sampling frame	1	0.55

NOTE: Total and eligible school counts are rounded to nearest ten. Percentages are based on unrounded counts. Detail may not sum to totals because of rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

The tables below present unweighted counts of sampled private schools by age, private school type and eligibility status.

Number of sampled private schools, long-term trend assessment, age 9, by private school type and eligibility status: 2022

Private school type	Eligibility status	Unweighted count of schools	Unweighted percentage
All Private	Total	160	100.00
	Eligible	140	82.93
	Ineligible	28	17.08
Catholic	Total	50	100.00
	Eligible	40	91.67
	Ineligible	4	8.83
Other Private	Total	120	100.00
	Eligible	90	79.31
	Ineligible	24	20.69
NOTE: Total and eligible school counts are rounded to nearest ten. Percentages are based on unrounded counts. Detail may not sum to total due to rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Number of sampled private schools, long-term trend assessment, age 13, by private school type and eligibility status: 2022

Private school type	Eligibility status	Unweighted count of schools	Unweighted percentage
All Private	Total	180	100.00
	Eligible	140	75.96
	Ineligible	44	24.04
Catholic	Total	60	100.00
	Eligible	52	67.74
NOTE: Total and eligible school counts are rounded to nearest ten. Percentages are based on unrounded counts. Detail may not sum to total due to rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Private school type Eligibility status Unweighted count of schools Unweighted percentage

	Ineligible	10	32.26
Other Private	Total	120	100.00
	Eligible	87	71.90
	Ineligible	34	28.10

NOTE: Total and eligible school counts are rounded to nearest ten. Percentages are based on unrounded counts. Detail may not sum to total due to rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/ineligible_private_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Sampling Frame for the 2022 Private School Long-Term Trend Assessment

The primary sampling frame for private schools was developed from the Private School Universe Survey (PSS) corresponding to the 2019– 2020 school year. The PSS file is the Department of Education’s primary database of elementary and secondary private schools in the 50 states and the District of Columbia, and it is based on a survey conducted by the U.S. Census Bureau during the 2019–2020 school year. This sampling frame is referred to as the PSS-based sampling frame.

The PSS-based sampling frame was restricted to schools located in the primary sampling units (PSUs) selected for the NAEP 2022 long-term

Age Distribution Fractions

New-School Sampling Frame

trend (LTT) assessment. In addition, the sampling frame excluded ungraded schools, vocational schools with no enrollment, special-education-only schools, homeschool entities, prison and hospital schools, and juvenile correctional institutions. Vocational schools with no enrollment serve students who split their time between the vocational school and their home school.

The following table presents the number of schools and estimated enrollment for the PSS-based sampling frame by age population. The unweighted estimated enrollment is restricted to the selected PSUs. The weighted estimated enrollment incorporates the PSU weight (inverse of the probability of selecting the PSU) and the estimated age-eligible enrollment, and thus is a national estimate of the number of private school students in the age population. The age-eligible enrollment was estimated using age distribution fractions (see link above right) derived by grade for each age population.

Number of schools and enrollment in private school sampling frame, long-term trend assessment, by age and affiliation: 2022

Age

Affiliation

Number of schools

Estimated enrollment (unweighted)

Estimated enrollment (weighted)

Age Affiliation Number of schools Estimated enrollment (unweighted) Estimated enrollment (weighted)

9	Total	12,090	212,540	334,060
	Catholic	2,788	76,511	118,126
	Non-Catholic	7,398	126,509	202,890
	Unknown affiliation	1,904	9,520	13,044
13	Total	12,749	213,077	333,894
	Catholic	31793	79,894	119,594
	Non-Catholic	7,467	123,668	201,261
	Unknown affiliation	1,903	9,575	13,039
NOTE: Detail may not sum to totals due to rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

For quality control purposes, school and student counts from the sampling frame were compared to school and student counts from previous private school frames by grade (for grades 4 and 8). Comparisons were grade-based because most NAEP assessments are grade-based, and grade counts are a reasonable proxy for age counts for comparison purposes. No major discrepancies were found.

A secondary sampling frame was also created for the age 9 sample to account for schools that newly opened or became newly eligible between the 2019–2020 and 2021– 2022 school years. This frame contains brand-new and newly-eligible schools expected to have 9 year olds and is referred to as the new-school sampling frame. Because there are no sources available to identify new schools for non-Catholic private schools, the new school frame for private schools contains only Catholic schools. Like the PSS-based frame, the new-school sampling frame was restricted to schools in the selected PSUs and certain types of schools were excluded from the frame as described above.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_frame_for_the_2022_private_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Age Distribution Fractions for the 2022 Private School Long-Term Trend (LTT) Assessment

Age distribution fractions are estimated proportions of students in each grade that are age-eligible for sampling. The fractions are components in the school measure of size. For ages 9 and 13, a breakout by every year of birth cohort represented in the relevant grades was fully carried out. The age distribution fractions for the 2020 LTT assessments were also used for 2022. The computation of the age distribution fractions for the age 9 and 13 assessments starts with estimates derived from the NAEP 2017 reading and mathematics assessments. For grades 4 and 8, estimates of the percentages of students by year of birth were computed separately for public and private schools by census region.

These estimates were determined by first computing the weighted counts of assessed, absent, and excluded students for the NAEP 2017 reading and mathematics assessments and then aggregating them. The student base weights were used for this purpose. The weighted aggregations are estimates of the total number of students by year of birth for grade 4 in the school year 2016–2017. The tables below present these estimates by region for fourth grade for private schools.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, private schools Northeast region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	59,000	1.00
2003	33	#
2004	33	#
2005	293	#
2006	16,000	0.26
2007	43,000	0.73
2008	335	0.01
2009	100	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, private schools Midwest region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	85,000	1.00
2005	785	0.01
2006	37,000	0.43
2007	48,000	0.56
2008	192	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, private schools South region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	108,000	1.00
2005	2,000	0.02
2006	42,000	0.39
2007	63,000	0.58
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Year of birth Weighted aggregations Weighted proportions

2008

524

# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, private schools West region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	60,000	1.00
2005	640	0.01
2006	20,000	0.34
2007	39,000	0.65
2008	263	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

The combined percentages of the reading and mathematics assessments are the best estimates of the percentages of fourth-graders in school year 2016–2017 by year of birth. The objective is to get the percentages of those born in a particular year (e.g., 2007) who are in grades 2, 3, 4, and 5. Since direct estimates are not available, an indirect estimate can be obtained by assuming that the other grades have the identical distribution as fourth grade, but moved back or moved forward by one year. This effectively assumes a stationary distribution of age and grade, which is only a rough approximation of reality, but it suffices to give good measures of size. The derived percentages by age and grade using this stationarity approximation are illustrated for the Northeast region in the table below.

Grade distribution for private schools Northeast region, 2016–2017 school year, assuming stationarity, by year of birth: 2017

Year of birth	Second grade	Third grade	Fourth grade	Fifth grade	Sixth grade
Total	1.00	1.00	1.00	1.00	1.00
2003	#	#	#	#	#
2004	#	#	#	#	0.26
2005	#	#	#	0.26	0.73
2006	#	#	0.26	0.73	0.01
2007	#	0.26	0.73	0.01	#
2008	0.26	0.73	0.01	#	#
2009	0.73	0.01	#	#	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

In distribution, the third-graders are exactly one year younger, the second-graders exactly two years younger, etc. If we read across the grade distribution for those born in 2007, we see that the percentages for second through sixth grades are equal to the percentages for 2005 through 2009 for fourth grade. The same logic was applied to all four tables provided above, yielding estimates of the percentages of nine year olds by grade that were used to compute school measures of size during the sampling of private schools.

Back to Top

A similar logic applied to the age 13 sample. For the age 13 sample, the starting point was the NAEP 2017 grade 8 reading and mathematics assessments. Aggregated estimates were computed in the same way as for the age 9 sample. The four tables below provide these estimates by region for eighth grade for public schools.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, private schools Northeast region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	63,000	1.00
2000	156	#
2001	621	0.01
2002	19,000	0.31
2003	42,000	0.67
2004	675	0.01
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, private schools Midwest region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	78,000	1.00
2001	992	0.01
2002	31,000	0.40
2003	45,000	0.58
2004	173	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, private schools South region, by year of birth: 2017

Year of birth

Weighted aggregations

Weighted proportions

Year of birth Weighted aggregations Weighted proportions

Total	111,000	1.00
2000	75	#
2001	2,000	0.02
2002	46,000	0.41
2003	63,000	0.57
2004	418	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, private schools West region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	52,000	1.00
2000	29	#
2001	503	0.01
2002	15,000	0.28
2003	37,000	0.70
2004	272	0.01
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/age_distribution_fractions_for_the_2022_private_school_long_term_trend_assessment.aspx

Shape62

NAEP Technical Documentation New-School Sampling Frame for the 2022 Private School Long-Term Trend Assessment

The NAEP 2022 private school frame was constructed using the most current Private School Universe Survey (PSS) file available from NCES. This file contained schools that were in existence during the 2019–2020 school year, (i.e., it was two years out of date). During the subsequent 2-year period, undoubtedly, some schools closed, some changed structure (one school becoming two schools, for example), some newly opened, and still others changed their grade span.

A diocese was considered to be small if it contained no more than one school at each of grades 4 and 8. During school recruitment, schools sampled from small dioceses were asked to identify schools within their dioceses that newly offered the targeted grades (grades 2-5 for age 9). From a sampling perspective, each new school was viewed as an "annex" to the sampled school, which meant that it had a well-defined probability of selection equal to that of the sampled school. When a school in a small diocese was sampled from the PSS frame, its associated new school was automatically sampled as well.

and including the first diocese at or above the 80th cumulative percentage were defined as large dioceses. The remaining dioceses were defined as medium dioceses.

A simplified example is given below. The dioceses are ordered by descending percentage enrollment. The first six become large dioceses and the last six become medium dioceses.

Example showing assignment of Catholic dioceses to the large-size and medium-size diocese strata, 2022

Diocese	Percentage enrollment	Cumulative percentage enrollment	Stratum
Diocese 1	20	20	L
Diocese 2	20	40	L
Diocese 3	15	55	L
Diocese 4	10	65	L
Diocese 5	10	75	L
Diocese 6	10	85	L
Diocese 7	5	90	M
Diocese 8	2	92	M
Diocese 9	2	94	M
Diocese 10	2	96	M
Diocese 11	2	98	M
Diocese 12	2	100	M
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Mathematics and Reading Assessments.

In actuality, there were 77 large and 96 medium dioceses in the sampling frame.

The target sample size was 10 dioceses total across the medium-size and large-size diocese strata: eight from the large-size diocese stratum and two from the medium-size diocese stratum.

NCEA was sent a listing of all the schools in the selected dioceses that appeared on the 2019–2020 PSS file and was asked to provide information about the new schools not included in the file and grade span changes of existing schools. These listings were used as sampling frames for selection of new Catholic schools and updates of existing schools, keeping in mind that grades 2-5 were targeted for age 9. In addition, the new-school frames were limited to the geographic areas covered by the sampled LTT primary sampling units (PSUs).

The following table presents the number and percentage of schools and average estimated age enrollment for the age 9 "new-school" frames by census region. For age 9 there were no new schools in the Midwest region.

Number and percentage of schools and mean school size in the private new-school frame, long-term trend assessment for age 9, by census region: 2022

Census region	Schools	Percentage	Mean school size
Total	15	100.00	32
Northeast	11	73.33	37
Midwest	0	0.00	0
South	3	20.00	11
West	1	6.67	35
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Mathematics and Reading Assessments.

For age 13 a private new-school frame was not constructed. Based on the 2022 experience with age 9, where only one of the new schools on the frame was sampled, it was decided not to conduct a private new-school procedure for age 13. Because the age 13 assessment was in a different school year than age 9, conducting the new-school procedure for age 13 would have required that the process described above be carried out anew, one year after the age 9 process was conducted.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/new_school_sampling_frame_for_the_2022_private_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Sampling of Private Schools for the 2022 Long- Term Trend Assessment

In designing the private school long-term trend samples for each age, six objectives underlie the process of determining the probability of selection for each school and the number of students to be sampled from each selected school:

to meet the overall target student sample size;

to select an equal-probability sample of students from each age population; to limit the number of students selected from any one school;

to ensure that the sample within a school does not include a very high percentage of the students in the school, unless all students are included;

to reduce the sampling rate of small schools, in recognition of the greater cost and burden per student of conducting assessments in such schools; and to ensure the inclusion of all eligible schools that were part of the 2020 private school long-term trend sample for each age, respectively.

The goal in determining the school's measure of size is to optimize across the second to the fifth objectives in terms of maintaining the precision of estimates and the cost effectiveness of the sample design.

The measures of size vary by enrollment size. The initial measures of size, $MOS_{js}$, were set as follows: \begin{equation} MOS_{js} = PSCHWT_{s} \times PSU\_WT_{s} \times \left\{\begin{array}{llll} x_{js}{,} & \text{if } z_{js} < x_{js} \\ y_{j}{,} & \text{if } 19 < x_{js} \leq z_{js}\\ \biggl(\dfrac{y_j}{20}\biggr) \times x_{js}{,} & \text{if } 10 < x_{js} \leq 19 \\ \dfrac{y_j}{2}{,} & \text{if } x_{js} \leq 10 \\ \end{array}\right. \end{equation}

where $PSCHWT_{s}$ is the Private School Universe Survey area frame weight for school $s$; $PSU\_WT_{s}$ is the PSU weight (i.e., the inverse of the PSU probability of selection) for school $s$; $x_{js}$ is the estimated age enrollment for school $s$ for sample age $j$; $y_{j}$ is the target within-school student sample size for

sample age $j$; and $z_{js}$ is the within-school take-all student cutoff for school $s$ for sample age $j$. The target within-school sample size and the within-school take- all cutoff were both 50.

The measures of size for schools in the Honolulu Primary Sampling Unit (PSU) were doubled to increase their chances of selection. Schools in the Honolulu PSU have their measures of size doubled to ensure at least one sampled school from the PSU. The Honolulu PSU is a certainty not due to its size, but because it is unique due to its high population of Asian and Native Hawaiian/Pacific Islander students. The preliminary measures of size $M_{js}$ for schools in the Honolulu PSU were set as \begin{equation} M_{js} = 2 \times MOS_{js}. \end{equation}

Preliminary measures of size for schools not in the Honolulu PSU were set equal to the initial measures of size.

The preliminary school measure of size is rescaled to create an expected number of hits by applying a multiplicative constant $b_{j}$, which varies by age $j$. One can choose a value of $b_{j}$ such that the expected overall student sample yield matches the desired target specified by the design, where the expected yield is calculated by summing the product of an individual school's probability and its student yield across all schools in the frame. For private schools, this parameter varied by private school affiliation (Catholic, non-Catholic, and unknown affiliation).

The final measure of size, $E_{js}$, is defined as

\begin{equation} E_{js}=min(b_{j}\times M_{js},u_{j}). \end{equation}

The quantity $u_{j}$ (the maximum number of hits allowed) in this formula is designed to put an upper bound on the burden for the sampled schools. For private schools, \ (u_{j}\) is 1 because by design a school could not be selected, or hit in the sampling process more than once for a given sample age.

To address the objective in the last bullet above, an adjustment was made to the initial measures of size in an attempt to ensure the inclusion of all eligible schools that were part of the 2020 private school long-term trend sample for each age. The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, maximized the overlap of schools selected for both the 2020 and 2022 long-term trend assessments.

Schools were ordered within each sampling stratum using the serpentine sort described under the stratification of private schools. A systematic sample was then drawn using this serpentine-sorted list and the measures of size. The numbers of private schools selected were approximately 160 for age 9 and 180 for age 13.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_of_private_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Stratification of Private Schools for the 2022 Long-Term Trend Assessment

For the private school sampling frame file at each age (9 or 13), schools were explicitly stratified by private school affiliation (Catholic, non-Catholic, and unknown affiliation). Private school affiliation was unknown for nonrespondents to the NCES Private School Universe Survey (PSS). Within private school type, separate implicit stratification schemes were used to sort schools in certainty primary sampling units (PSUs) and noncertainty PSUs. In all cases, the implicit stratification was achieved via a "serpentine sort".

Within each certainty PSU, the schools were hierarchically sorted by census region;

urbanization classification (four categories based on urban-centric locale); and estimated age-specific enrollment.

Schools in noncertainty PSUs were hierarchically sorted by PSU stratum;

urbanization classification (four categories based on urban-centric locale); and estimated age-specific enrollment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_of_private_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Student Sample Selection for the 2022 Private School Long-Term Trend Assessment

Students in private schools were selected in the same way as students in the public schools, except that there was no oversampling of Black, Hispanic, and American Indian/Alaska Native students.

About 37 percent of the participating private schools submitted student lists through E-filing, and the remaining 63 percent submitted paper lists.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_sample_selection_for_the_2022_private_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Substitute Private Schools for the 2022 Long- Term Trend Assessment

Substitutes were preselected for the private school samples by sorting the school frame file for each of ages 9 and 13 according to the actual order used in the sampling process (the implicit stratification). For operational reasons, the original selection order was embedded within the sampled primary sampling unit (PSU) and state. Each sampled school with known affiliation had each of its nearest neighbors within the same sampling stratum on the school frame file identified as a potential substitute. Sampled schools with unknown affiliation were not assigned substitutes. Since age-specific enrollment was used as the last sort ordering variable, the nearest neighbors had age-specific enrollment values very close to that of the sampled school. This was done to facilitate the selection of about the same number of students within the substitute as would have been selected from the original sampled school.

Schools were disqualified as potential substitutes if they were already selected in any of the original private school samples, assigned as a substitute for another private school (earlier in the sort ordering), or were not the same affiliation as the originally sampled school.

If both nearest neighbors were still eligible to be substitutes, the one with a closer age-specific enrollment was chosen. If both nearest neighbors were equally distant from the sampled school in their age-specific enrollment (an uncommon occurrence), one of the two was randomly selected.

Of the approximately 160 originally sampled private schools for age 9, about 80 schools had a substitute activated because the original eligible school did not participate, and a handful of those activated substitutes participated. For age 13, of the approximately 180 originally sampled private schools, about 80 also had a substitute activated because the original eligible school did not participate. Similar to age 9, only a handful of activated substitutes for age 13 participated.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/substitute_private_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Target Population of the 2022 Private School Long-Term Trend Assessment

The target populations for the 2022 long-term trend private school assessments included all students who were age 9 (i.e., born in 2012) or age 13 (born in 2009) in private schools in the 50 states and the District of Columbia.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/target_population_of_the_2022_private_school_long_term_trend_assessment.aspx

NAEP Technical Documentation 2022 Public School Long-Term Trend Assessment

The NAEP 2022 sample design yielded nationally representative samples of public school students at ages 9 and 13 for long-term trend (LTT) through a three-stage approach:

selection of primary sampling units (PSUs); selection of schools within strata; and

selection of students within schools.

The sample of schools was selected with probability proportional to a measure of size based on the estimated age enrollment in the schools.

The 2022 sampling plan was designed to assess 14,760 students at each age in public schools for LTT. These students were allocated among tests in mathematics and reading. Target sample sizes were adjusted to reflect expected public school and student response and eligibility.

Schools on the sampling frame were explicitly stratified prior to sampling by PSU type (certainty/noncertainty). Within certainty PSUs, schools were implicitly stratified by census region, American Indian/Alaska Native (AI/AN) stratum, urbanization classification, race/ethnicity

Target Population Sampling Frame Stratification of Schools Sampling of Schools Substitute Schools Ineligible Schools Student Sample Selection

stratum, and race/ethnicity percentage. Within noncertainty PSUs, schools were implicitly stratified by PSU stratum, AI/AN stratum, urbanization classification, and race/ethnicity percentage. Note that the use of the AI/AN stratum as an implicit stratification variable helped ensure that a reasonable number of schools with sufficient numbers of AI/AN students in them were selected.

From the stratified frame of public schools, systematic random samples of age-eligible schools were drawn with probability proportional to a measure of size based on the estimated age enrollment of the school for the relevant age. The measures of size included an adjustment made in an attempt to ensure the inclusion of all eligible schools that were part of the 2020 public school long-term trend sample for ages 9 and 13. The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, maximized the overlap of schools selected for both the 2020 and 2022 long-term trend assessments at each age.

Additionally, AI/AN, Black, and Hispanic students were oversampled at moderate rates as follows. First, schools in a high AI/AN stratum (i.e., schools with at least five percent AI/AN students and at least five AI/AN students at the sample age) were sampled at four times the rate (by quadrupling their measure of size) as schools not in a high AI/AN stratum to implement oversampling of AI/AN students. Second, schools not in a high AI/AN stratum but in a high Black/Hispanic stratum (i.e., schools that were not oversampled for AI/AN students and with at least 15 percent Black/Hispanic students and at least 10 Black/Hispanic students at the sample age) were sampled at twice the rate (by doubling their measure of size) as schools not in a high Black/Hispanic stratum to implement oversampling of Black and Hispanic students. This approach is effective in increasing the sample sizes of AI/AN, Black, and Hispanic students without inducing undesirably large design effects on the sample, either overall or for particular subgroups.

Finally, schools in the Honolulu PSU were oversampled at twice the rate (by doubling their measure of size) as schools not in the Honolulu PSU. This was done to ensure at least one school was sampled from this PSU. At least one school was sampled because the total measure of size for all schools in Honolulu exceeded the sampling interval. The PSU was selected with certainty not due to its size, but because it is unique due to its high population of Asian and Native Hawaiian/Pacific Islander students.

Each selected school in the public school sample provided a list of age-eligible enrolled students from which a systematic sample of students was drawn. Within each school, students of the same race/ethnicity were selected with equal probability.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/2022_public_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Ineligible Public Schools for the 2022 Long-Term Trend Assessment

The Common Core of Data (CCD) public school file from which most of the sampled schools were drawn corresponds to the 2019–2020 school year for age 9 and 2020–2021 for age 13, one and two years prior to the assessment school year. During the intervening period, some of these schools either closed, no longer offered the grades corresponding to the sample age of interest, or became ineligible for other reasons. In such cases, the sampled schools were considered to be ineligible.

The table below presents unweighted counts of sampled public schools by eligibility status, including the reason for ineligibility.

Number of sampled public schools, long-term trend assessment, by eligibility status within age: 2022

Eligibility Status	Unweighted count of schools	Unweighted percentage
All age 9 sampled public schools	410	100.00
Eligible schools	400	96.62
No age-eligible students	7	1.69
School closed	5	1.21
Not a regular school	2	0.48
Other ineligible school	0	0.00
Duplicate on sampling frame	0	0.00
All age 13 sampled public schools	500	100.00
Eligible schools	460	92.00
No age-eligible students	26	5.20
School closed	6	1.20
Not a regular school	9	1.80
Other ineligible school	1	0.20
Duplicate on sampling frame	0	0.00
NOTE: Total and eligible school counts are rounded to nearest ten. Percentages are based on unrounded counts. Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/ineligible_public_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Sampling Frame for the 2022 Public School Long- Term Trend Assessment

Drawing the school samples for the 2022 assessment required a comprehensive list of public schools in each jurisdiction containing information for stratification purposes. As in previous NAEP assessments, the Common Core of Data (CCD) file developed by NCES was used to construct the sampling frame. The CCD file corresponding to the 2019–2020 school year provided the frame for all regular public (as classified by the CCD), state-operated public (as classified by the CCD), Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools serving age 9 in the 50 states and the District of Columbia. The school frame for age 13 was based on the CCD file corresponding to the 2020–2021 school year.

The respective sampling frames were restricted to schools located in the primary sampling units (PSUs) selected for the NAEP 2022 long-term

Age Distribution Fractions

New-School Sampling Frame

trend (LTT) assessment. In addition, the sampling frames excluded ungraded schools, vocational schools with no enrollment, special-education-only schools, homeschool entities, prison or hospital schools, and juvenile correctional institutions. Vocational schools with no enrollment serve students who split their time between the vocational school and their home school.

The public school frame for the LTT assessment for age 9 contained approximately 29,000 schools. The estimated age 9 enrollment (unweighted) for these schools was 2.17 million and the estimated age 9 enrollment (weighted) was 3.71 million. The unweighted estimated enrollments are restricted to the selected PSUs for LTT. The weighted estimated enrollments incorporate the PSU weight (inverse of the probability of selecting the PSU), and thus are national estimates of the number of public school students for the age 9 population. The age-eligible enrollment was estimated using age distribution fractions (see link above right) derived by grade for the age 9 population. The school frame for age 13 contained approximately 25,000 schools. The unweighted estimated age 13 enrollment was 2.20 million, and the weighted estimated age 13 enrollment was

3.77 million.

For quality control purposes, school and student counts from the sampling frame were compared to school and student counts from previous public school frames by

grade (grade 4 for age 9 and grade 8 for age 13). Comparisons were grade-based because most NAEP assessments are grade-based, and grade counts are a reasonable proxy for age counts for comparison purposes. No major discrepancies were found.

A secondary sampling frame was also created for each age to account for schools that newly opened or became newly eligible between the 2019–2020 school year and the school year at the time of assessment (2021–2022 for age 9 and 2022–2023 for age 13). This frame contains brand-new and newly-eligible schools expected to have 9 (or 13) year olds, and is referred to as the new-school sampling frame. Like the CCD-based frame, the new-school sampling frame is restricted to schools in the selected PSUs and certain types of schools were excluded from the frame as described above.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_frame_for_the_2022_public_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Age Distribution Fractions for the 2022 Public School Long-Term Trend (LTT) Assessment

Age distribution fractions are estimated proportions of students in each grade that are age-eligible for sampling. The fractions are components in the school measure of size. For ages 9 and 13 a breakout by every year of birth cohort represented in the relevant grades was fully carried out. The age distribution fractions for the 2020 LTT assessments were also used for 2022. The computation of the age distribution fractions for the age 9 and 13 assessments starts with estimates derived from the NAEP 2017 reading and mathematics assessments. For grades 4 and 8, estimates of the percentages of students by year of birth were computed separately for public and private schools by census region.

These estimates were determined by first computing the weighted counts of assessed, absent, and excluded students for the NAEP 2017 reading and mathematics assessments and then aggregating them. The student base weights were used for this purpose. The weighted aggregations are estimates of the total number of students by year of birth for grade 4 or 8 in the school year 2016–2017. The tables below present these estimates by region for fourth grade for public schools.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, public schools Northeast region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	578,000	1.00
2003	21	#
2004	160	#
2005	6,000	0.01
2006	161,000	0.28
2007	409,000	0.71
2008	877	#
2009	25	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, public schools Midwest region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	765,000	1.00
2003	16	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

2004	319	#
2005	11,000	0.01
2006	304,000	0.40
2007	448,000	0.59
2008	832	#
2009	55	#

# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, public schools South region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	1,506,000	1.00
2003	32	#
2004	2,000	#
2005	47,000	0.03
2006	603,000	0.40
2007	853,000	0.57
2008	2,000	#
2009	8	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 4 reading and mathematics assessments, public schools West region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	896,000	1.00
2003	1	#
2004	123	#
2005	5,000	0.01
2006	250,000	0.28
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

2007	639,000	0.71
2008	1,000	#
2009	14	#

# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Grade distribution for public schools Northeast region, 2016–2017 school year, assuming stationarity, by year of birth: 2017

Year of birth	Second grade	Third grade	Fourth grade	Fifth grade	Sixth grade
Total	1.00	1.00	1.00	1.00	1.00
2003	#	#	#	#	0.01
2004	#	#	#	0.01	0.28
2005	#	#	0.01	0.28	0.71
2006	#	0.01	0.28	0.71	#
2007	0.01	0.28	0.71	#	#
2008	0.28	0.71	#	#	#
2009	0.71	#	#	#	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Back to Top

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, public schools Northeast region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	569,000	1.00
1999	35	#
2000	737	#
2001	11,000	0.02
2002	165,000	0.29
2003	391,000	0.69
2004	2,000	#
2005	73	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2020 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, public schools Midwest region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	753,000	1.00
1999	223	#
2000	410	#
2001	14,000	0.02
2002	305,000	0.40
2003	433,000	0.57
2004	1,000	#
2005	43	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2020 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, public schools South region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	1,384,000	1.00
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2020 Long-Term Trend Assessment.

Year of birth Weighted aggregations Weighted proportions

1999	125	#
2000	3,000	#
2001	59,000	0.04
2002	553,000	0.40
2003	766,000	0.55
2004	3,000	#
2005	108	#
2006	1	#

# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2020 Long-Term Trend Assessment.

Weighted aggregations and proportions from the grade 8 reading and mathematics assessments, public schools West region, by year of birth: 2017

Year of birth	Weighted aggregations	Weighted proportions
Total	869,000	1.00
1999	6	#
2000	103	#
2001	8,000	0.01
2002	247,000	0.28
2003	612,000	0.70
2004	2,000	#
2005	45	#
# Rounds to zero.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2020 Long-Term Trend Assessment.

Back to Top

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/age_distribution_fractions_for_the_2022_public_school_long_term_trend_assessment.aspx

NAEP Technical Documentation New-School Sampling Frame for the 2022 Public School Long-Term Trend Assessment

The primary sampling frames for the 2022 public school samples for the long-term trend (LTT) assessments in mathematics and reading were constructed using the most current Common Core of Data (CCD) files available from NCES. For age 9, this file contained schools that were in existence during the 2019–2020 school year (i.e., it was two years out of date). Similarly, for age 13, this file contained schools that were in existence during the 2020–2021 school year (also about two years out of date, given the fall 2022 assessment date for age 13). During the subsequent 2-year periods, undoubtedly some schools closed, some changed structure (one school becoming two schools, for example), some newly opened, and still others changed their grade span.

A supplemental sample was selected from a list of schools that were new or had become newly eligible sometime after the school year represented by the CCD (2019–2020 for age 9, and 2020–2021 for age 13). The goal was to allow every new school a chance of selection, thereby fully covering the target population of schools in operation during the school year at the time of assessment (2021–2022 for age 9, and 2022–2023 for age 13). It was infeasible to ask every school district in the United States to provide a supplemental school frame, so a two-stage procedure was employed. First, a sample of school districts was selected within each state. Then each State or Trial Urban District Assessment (TUDA) Coordinator was sent a list of the schools within their sampled districts that had been present on the 2019–2020 CCD file. The Coordinators were asked to add in any new schools and identify any schools on this list that had become newly eligible.

The new-school process began with the preparation of a district-level frame. The starting point was a file containing every public school district in the United States. The new- school process for LTT ages 9 and 13 piggybacked on the process for the grade-based samples as follows:

Specific districts were designated as in sample with certainty. They included the following districts: districts in jurisdictions where all schools were selected for sample;

state-operated districts;

districts in states with fewer than 10 districts;

charter-only districts (that is, districts containing no schools other than charter schools); and TUDA districts.

Then noncertainty districts were classified as small, medium, or large based on the number of schools and student enrollment of schools from the CCD-based public school frame.

A district was considered to be small if it contained no more than one school at each of grades 4 and 8. During school recruitment, the Coordinators were asked to identify schools within their small districts that newly offered the targeted grades (grades 2-5 for age 9, and grades 6-9 for age 13). From a sampling perspective, each new school was viewed as an “annex” to the sampled school, which meant that it had a well-defined probability of selection equal to that of the sampled school. When a school in a small district was sampled from the CCD-based frame, its associated new school was automatically sampled as well.

Within each jurisdiction, districts that were neither certainty selections nor small were divided into two strata, one containing large-size districts and a second containing medium-size districts. These strata were defined by computing the percentage of jurisdiction enrollment represented by each district, sorting in descending order, and cumulating the percentages. All districts up to and including the first district at or above the 80th cumulative percentage were defined as large districts. The remaining districts were defined as medium districts.

A simplified example is given below. The state's districts are ordered by descending percentage enrollment. The first six become large districts and the last six become medium districts.

Large-size and medium-size district strata example, by enrollment, stratum, and district, 2022

District	Percentage enrollment	Cumulative percentage enrollment	Stratum
1	20	20	L
2	20	40	L
3	15	55	L
4	10	65	L
5	10	75	L
6	10	85	L
7	5	90	M
8	2	92	M
9	2	94	M
10	2	96	M
11	2	98	M
12	2	100	M
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Mathematics and Reading Assessments.

The selected districts in each jurisdiction were then sent a listing of all their schools that appeared on the 2019–2020 CCD file and were asked to provide information about the new schools not included in the file and grade span changes of existing schools. These listings provided by the selected districts were used as sampling frames for selection of new public schools and updates of existing schools. This process was conducted through the NAEP State or TUDA Coordinator in each jurisdiction. The Coordinators were sent the information for all sampled districts in their respective jurisdictions and were responsible for returning the completed updates. Any new schools reported by the states with one or more of the grades 2-5 were eligible for the age 9 assessments. Any new schools reported by the states with one or more of the grades 6-9 were eligible for the age 13 assessments, provided another condition was met. That condition was that the new school was not already on the CCD file used to construct the age 13 school frame. Since that CCD file was one year newer than the one used for all the other NAEP 2022 samples, this condition was necessary. In addition, the LTT new-school frames were limited to the geographic areas covered by the sampled LTT primary sampling units (PSUs).

The following tables present the number and percentage of schools and average estimated age enrollment for the LTT new-school frames by census region for each age.

Number and percentage of schools and mean school size in the public new-school frame, long-term trend assessment for age 9, by census region: 2022

Census region

Schools

Percentage

Mean school size

Census region Schools Percentage Mean school size

Total	183	100.00	42
Northeast	22	12.02	10
Midwest	37	20.22	20
South	92	50.27	45
West	32	17.49	51
NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Mathematics and Reading Assessments.

Number and percentage of schools and mean school size in the public new-school frame, long-term trend assessment for age 13, by census region: 2022

Census region	Schools	Percentage	Mean school size
Total	266	100.00	20
Northeast	42	15.79	12
Midwest	64	24.06	10
South	97	36.47	24
West	63	23.68	27
NOTE: Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/new_school_sampling_frame_for_the_2022_public_school_long_term_trend_assessment.aspx

NAEP Technical Documentation Sampling of Public Schools for the 2022 Long- Term Trend Assessment

In designing the public school long-term trend sample for each age, seven objectives underlie the process of determining the probability of selection for each school and the number of students to be sampled from each selected school:

to meet the overall target student sample size;

to select an equal-probability sample of students from the age population; to limit the number of students selected from any one school;

to ensure that the sample within a school does not include a very high percentage of the students in the school, unless all students are included;

to reduce the sampling rate of small schools, in recognition of the greater cost and burden per student of conducting assessments in such schools; to increase the number of American Indian/Alaska Native (AI/AN), Black, and Hispanic students in the sample; and

to ensure the inclusion of all eligible schools that were part of the 2020 public school long-term trend sample for each age, respectively.

The measures of size vary by enrollment size. The initial measures of size, $MOS_{js}$, were set as follows: \begin{equation} MOS_{js} = PSU\_WT_{s} \times \left\

{\begin{array}{llll} x_{js}{,} & \text{if } z_{js} < x_{js} \\ y_{j}{,} & \text{if } 19 < x_{js} \leq z_{js}\\ \biggl(\dfrac{y_j}{20}\biggr) \times x_{js}{,} & \text{if } 10 < x_{js} \leq 19 \\ \dfrac{y_j}{2}{,} & \text{if } x_{js} \leq 10 \\ \end{array}\right. \end{equation}

where $PSU\_WT_{s}$ is the PSU weight (i.e., the inverse of the PSU probability of selection) for school $s$; $x_{js}$ is the estimated age enrollment for school $s$ for sample age $j$; $y_{j}$ is the target within-school student sample size for sample age $j$; and $z_{js}$ is the within-school take-all student cutoff for school $s$ for sample age $j$. The target within-school sample size and the within-school take-all cutoff were both 50.

To increase the number of AI/AN students in the sample, the measures of size for schools with relatively high proportions of AI/AN students (5 percent or more and with at least 5 AI/AN students) were quadrupled. The preliminary measures of size $M_{js}$ for these schools were set as \begin{equation} M_{js} = 4 \times MOS_{js}.

\end{equation}

Likewise, to increase the number of Black and Hispanic students in the sample, the measures of size for schools with relatively high proportions of Black/Hispanic students (15 percent or more and with at least 10 Black/Hispanic students) were doubled if they had not already been quadrupled due to AI/AN enrollment. The preliminary measures of size

$M_{js}$ for these schools were set as \begin{equation} M_{js} = 2 \times MOS_{js}. \end{equation}This approach is effective in increasing the sample sizes of AI/AN, Black, and Hispanic students without inducing undesirably large design effects on the sample, either overall, or for particular subgroups.

The measures of size for schools in the Honolulu primary sampling unit (PSU) were doubled to increase their chances of selection. Schools in the Honolulu PSU have their measures of size doubled to ensure at least one sampled school from the PSU. The Honolulu PSU is a certainty not due to its size, but because it is unique due to its high population of Asian and Native Hawaiian/Pacific Islander students. The preliminary measures of size $M_{js}$ for schools in the Honolulu PSU were set as \begin{equation} M_{js} = 2 \times MOS_{js}. \end{equation}

Preliminary measures of size were set equal to the initial measures of size for schools whose measures of size were not doubled or quadrupled.

The final measure of size, $E_{js}$, is defined as

\begin{equation} E_{js}=min(b_{j}\times M_{js},u_{j}). \end{equation}

The quantity $u_{j}$ (the maximum number of hits allowed) in this formula is designed to put an upper bound on the burden for the sampled schools. For public schools, \ (u_{j}\) is 1 because by design a school could not be selected, or hit in the sampling process more than once for the given sample age.

In addition, new and newly-eligible schools were sampled from the new school frame. The final measure of size for these schools, $E_{js}$ is defined as

\begin{equation} E_{js}=min(b_{j}\times M_{js} \times \pi_{djs}^{-1},u_{j}). \end{equation}

The variable $\pi_{djs}$ is the probability of selection of the district $d$ into the new-school district sample.

To address the objective in the last bullet above, an adjustment was made to the initial measures of size in an attempt to ensure the inclusion of all eligible schools that were part of the 2020 public school long-term trend sample for each age. The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, maximized the overlap of schools selected for both the 2020 and 2022 long-term trend assessments.

Schools were ordered within each jurisdiction using the serpentine sort described under the stratification of public schools. A systematic sample was then drawn using this serpentine-sorted list and the measures of size. The numbers of public schools selected were approximately 410 for age 9 and 480 for age 13.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_of_public_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Stratification of Public Schools for the 2022 Long- Term Trend Assessment

For the public school sampling frame file for each of the ages 9 and 13, separate implicit stratification schemes were used to sort schools in certainty primary sampling units (PSUs) and noncertainty PSUs. The implicit stratification was achieved via a "serpentine sort."

For certainty PSUs, the schools were hierarchically sorted by census region;

American Indian/Alaska Native (AI/AN) stratum (two categories based on percentage of AI/AN students); urbanization classification (four categories based on urban-centric locale);

race/ethnicity stratum; and race/ethnicity percentage.

The two categories within the AI/AN stratum were defined as follows. High AI/AN schools were schools with at least five percent AI/AN students and at least five AI/AN students in the sample age. Low AI/AN schools were those not designated as high AI/AN.

For schools in the high AI/AN stratum, if there were fewer than six expected sampled schools for a particular urbanization classification cell (nested within the AI/AN stratum and census region), the cell was collapsed with a neighboring urbanization classification cell. No race/ethnicity strata were generated. The final sort variable was total percentage of AI/AN students. Note the lower limit of six was chosen to facilitate the construction of nonresponse adjustment classes with sufficient numbers of schools and students in them.

For schools in the low AI/AN stratum, if there were fewer than six expected sampled schools for a particular urbanization classification cell (nested within the AI/AN stratum and census region), the cell was collapsed with a neighboring urbanization classification cell. If the expected sampled schools exceeded 12, then the race/ethnicity strata were defined based on the total percentage of Black, Hispanic, and AI/AN students. The strata were defined so that there were at least six expected sampled schools for each race/ethnicity stratum. Within each race/ethnicity stratum, the final sort variable was total percentage of Black, Hispanic, and AI/AN students. If the urbanization classification stratum had an expected sample size less than 12, no race/ethnicity strata were generated, and the final sort variable was total percentage of Black, Hispanic, and AI/AN students.

Schools in noncertainty PSUs were hierarchically sorted by

PSU stratum;

AI/AN stratum (two categories based on percentage of AI/AN students);

urbanization classification (four categories based on urban-centric locale); and race/ethnicity percentage.

The collapsing of cells within the noncertainty PSUs was implemented in a fashion similar to that described for certainty PSUs.

For schools in the high AI/AN stratum, the final sort variable was total percentage of AI/AN students. For schools in the low AI/AN stratum, the final sort variable was total percentage of Black, Hispanic, and AI/AN students.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_of_public_schools_for_the_2022_long_term_trend_assessment.aspx

Shape84

NAEP Technical Documentation Student Sample Selection for the 2022 Public School Long-Term Trend Assessment

The sampling of students for the public school assessments involved two steps: (1) sampling of students of the targeted age (9 or 13) from each sampled school, and (2) assignment of assessment subject (mathematics or reading) to the sampled students.

Sampling Students within Sampled Schools

All age-eligible students in the school were sampled if the school had 50 or fewer students of that age. Otherwise, a sample of 50 students was selected without replacement.

To increase the numbers of Black, Hispanic, and American Indian/Alaska Native (AI/AN) students in the assessment, students who were Black, Hispanic, or AI/AN were oversampled in some public schools. In particular, up to 5 extra Black, Hispanic, or AI/AN students were selected in public schools that were in both the low Black/Hispanic stratum and the low AI/AN stratum for school sampling. Such schools had less than 15 percent (and less than 10) Black/Hispanic students in the sample age, and less than 5 percent (and less than 5) AI/AN students in the sample age. In these schools only, and only if the school E-filed (see next paragraph), a special sampling procedure was implemented that required selecting the Black, Hispanic, and AI/AN students separately from the non-Black, non-Hispanic, non-AI/AN students using two different sampling rates. Within each school, a cap was placed on the sampling rate of the Black, Hispanic, and AI/AN students so that it was no more than twice the sampling rate for the other students. This oversampling was implemented in about 130 public schools.

Within each sampled school, a sample of students was selected from a list of students who were of the targeted age. The student lists were submitted either electronically using a system known as E-filing or on paper. In E-filing, student lists are submitted as Excel files by either School Coordinators, NAEP State Coordinators, or NAEP TUDA Coordinators. The files can be submitted for one school at a time (known as single school E-file submission) or for an entire jurisdiction at once (known as multiple school E- file submission). E-filing allows schools to easily submit student demographic data electronically with the student lists, easing the burden on field supervisors and school coordinators. The E-filing process for 2022 included an additional feature related to age-based sampling. To ease the burden on schools, schools could electronically submit all enrolled students for sampling, rather than just the age-eligible students. Students who were not age-eligible were removed from these lists before sampling.

Schools that are unable to submit their student lists using the E-filing system provide hardcopy lists to NAEP field supervisors. In 2022, about 99 percent of the participating public schools E-filed their student lists, and the remaining one percent submitted hardcopy lists.

In year-round multi-track schools, students in tracks scheduled to be on-break on the assessment day were removed from the student lists prior to sampling. Student base weights were adjusted to account for these students.

The sampling process was the same, regardless of list submission type. The sampling process was systematic (e.g., if the sampling rate was one-half, a random starting point of one or two was chosen, and every other student on the list was selected). For E-filed schools only, where demographic data were submitted for every student in the school, students were sorted by gender and race/ethnicity before the sample was selected to implicitly stratify the sample.

Assigning Assessment Subject to Sampled Students

Sampled students in each participating sampled school were assigned to either mathematics or reading. Within each school, about half of the sampled students were assigned to mathematics and half to reading using a process known as spiraling. In this process, test booklets were randomly assigned to sampled students from booklet sets that had, on average, mathematics to reading spiraling ratios of 1:1.

Similarly to the 2020 long-term trend assessment, for the 2022 assessment, newly identified students (including new enrollees), were not identified and added to the sample. The rationale for this decision was that due to the staggered field periods for the age-based assessment, student lists would be collected closer to assessment day than typically occurs for grade-based assessments.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_sample_selection_for_the_2022_public_school_long_term_trend_assessment.aspx

Shape85

NAEP Technical Documentation Substitute Public Schools for the 2022 Long-Term Trend Assessment

Substitutes were preselected for the public school samples by sorting the school frame file for each of ages 9 and 13 according to the actual order used in the sampling process (the implicit stratification). For operational reasons, the original selection order was embedded within the sampled primary sampling unit (PSU) and state. Each sampled school had each of its nearest neighbors within the same sampling stratum on the school frame file identified as a potential substitute. Because race/ethnicity percentage was used as the last sort ordering variable, the nearest neighbors had race/ethnicity percentage values very close to that of the sampled school. This helped ensure that expected yields of students in the oversampled race/ethnicity groups were maintained when originally sampled schools were replaced by their substitutes.

Schools were disqualified as potential substitutes if they were already selected in any of the original public school samples or assigned as a substitute for another public school (earlier in the sort ordering).

If both nearest neighbors were still eligible to be substitutes, the one with a closer age enrollment was chosen. If both nearest neighbors were equally distant from the sampled school in their age enrollment (an uncommon occurrence), one of the two was randomly selected.

Of the approximately 410 originally sampled public schools for age 9, about 30 schools had a substitute activated because the original eligible school did not participate, and a handful of those activated substitutes participated. For age 13 the corresponding numbers were approximately 460 originally sampled schools, with approximately 30 substitutes activated. Similar to age 9, only a handlful of activated substitutes participated for age 13.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/substitute_public_schools_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Target Population of the 2022 Public School Long- Term Trend Assessment

The target populations for the 2022 long-term trend public school assessments included all students who were age 9 (i.e., born in 2012) and age 13 (born in 2009) in public schools, Bureau of Indian Education (BIE) schools, and Department of Defense Education Activity (DoDEA) schools located in the 50 states and the District of Columbia.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/target_population_of_the_2022_public_school_long_term_trend_assessment.aspx

Shape87

NAEP Technical Documentation School and Student Participation Results for the 2022 Long-Term Trend Assessment

Participation in NAEP is not mandatory. Although a portion of the participating school sample consisted of substitute schools, it is preferable to calculate school response rates on the basis of school participation before substitution.

In every NAEP survey, some of the sampled students are not assessed. Examples of such students are as follows: withdrawn students;

excluded students with disabilities (SD); excluded English learner (EL) students;

students absent from both the original session and the makeup session (not excluded but not assessed); or full-time remote students.

Withdrawn students are those who have left the school before the original assessment. Excluded students were determined by their school to be unable to meaningfully take the NAEP assessment in their assigned subject, even with an accommodation. Excluded students must also be classified as SD and/or EL. Other students who were absent for the initial session can be assessed in the

School Response Rates for the 2022 Long-Term Trend Assessment

Student Response and Exclusion Rates for the Long-Term Trend Mathematics Assessment

Student Response and Exclusion Rates for the Long-Term Trend Reading Assessment

makeup session. The second-to-the-last category includes students who were not excluded (i.e., were to be assessed) but were not assessed, either due to absence from both sessions or because of a refusal to participate. Full-time remote students are enrolled in brick-and-mortar schools but do not attend school in person. They are considered not assessable for NAEP.

Assessed students are also classified as assessed without an accommodation or assessed with an accommodation. The latter group can be divided into SD students assessed with an accommodation, EL students assessed with an accommodation, or students who are both SD and EL and accommodated. Note that some SD and EL students are assessed without accommodations, and students who are neither SD nor EL can only be assessed without an accommodation.

The weighted student response rates utilize the student base weights and indicate the weighted percentage of assessed students among all students to be assessed. The exclusion rates, in contrast, provide the weighted percentage of excluded SD or EL students among all eligible students, i.e., absent, assessed, and excluded students. The weighted student full-time remote rates provide the weighted percentage of the student population that are full-time remote.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_and_student_participation_results_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation School Response Rates for the 2022 Long-Term Trend Assessment

The following table presents counts of eligible sampled schools and participating schools, as well as weighted school response rates, for the 2022 age 9 and 13 long-term trend assessments. The weighted school response rates estimate the proportion of the student population that is represented by the participating school sample prior to substitution.

Eligible and participating school counts and weighted school response rates, long-term trend mathematics and reading assessments, by age, school type, and census region: 2022

Age	School type and census region	Number of eligible sampled schools	Number of participating schools	Weighted school response rates prior to substitution (percent)
9	National all¹	540	410	85.93
	National public	400	370	90.45
	Northeast public	60	50	94.29
	Midwest public	70	60	76.17
	South public	170	170	98.86
	West public	100	90	85.64
	National private	140	50	32.02
	Catholic	40	30	62.73
	Non-Catholic	90	20	13.88
¹Includes national public, national private, Bureau of Indian Education, and Department of Defense Education Activity schools located in the United States.

NOTE: National public includes students from public schools only. It includes charter schools, but excludes Bureau of Indian Education schools and Department of Defense Education Activity schools. It is used when comparing national data to those of states, urban districts, or regions. School counts are rounded to nearest ten. Detail may not sum to totals because of rounding. Percentages are based on unrounded counts.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Age

School type and census region

Number of eligible sampled schools

Number of participating schools

Weighted school response rates prior to substitution (percent)

13	National all¹	580	460	85.98
	National public	440	400	89.81
	Northeast public	60	50	86.80
	Midwest public	80	70	88.08
	South public	190	180	90.99
	West public	110	100	91.15
	National private	140	60	40.35
	Catholic	50	40	82.98
	Non-Catholic	90	20	12.54

¹Includes national public, national private, Bureau of Indian Education, and Department of Defense Education Activity schools located in the United States. NOTE: National public includes students from public schools only. It includes charter schools, but excludes Bureau of Indian Education schools and Department of Defense Education Activity schools. It is used when comparing national data to those of states, urban districts, or regions. School counts are rounded to nearest ten. Detail may not sum to totals because of rounding. Percentages are based on unrounded counts.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_response_rates_for_the_2022_long_term_trend_assessment.aspx

NAEP Technical Documentation Student Response and Exclusion Rates for the 2022 Long-Term Trend Mathematics Assessment

The following table presents the weighted student response, exclusion, and full-time remote rates for the 2022 ages 9 and 13 long-term trend mathematics assessments. The exclusion rates give the percentage excluded, among all eligible (i.e., assessed, absent, or excluded) students. Excluded students must be either students with disabilities (SD) or English learners (EL). The response rates indicate the percentage of students assessed among those who it was intended would take the assessment from within the participating schools. Thus, students who were excluded are not included in the denominators of the response rates. The weighted student full-time remote rate indicates the percentage of the student population that is full-time remote (enrolled in brick-and-mortar schools but do not attend school in person).

Weighted student response, exclusion, and full-time remote rates, long-term trend public and private schools, national mathematics assessment, by age, school type, and census region: 2022

Age

School type and census region

Weighted student response rates

(percent)

Weighted percentage of all

eligible students who are SD and excluded

Weighted percentage of all

eligible students who are EL and excluded

Weighted student full-time remote

rates (percent)

Age

School type and census region

Weighted student response rates

(percent)

Weighted percentage of all

eligible students who are SD and excluded

Weighted percentage of all

eligible students who are EL and excluded

Weighted student full-time remote

rates (percent)

9	National all¹	87.08	1.55	0.63	0.71
	National public	86.96	1.67	0.68	0.76
	Northeast public	82.93	2.50	0.64	0.51
	Midwest public	87.88	1.53	0.28	0.64
	South public	88.34	1.36	0.48	1.05
	West public	86.46	1.77	1.42	0.53
	National private	90.42	0.12	#	0.17
	Catholic	93.25	0.31	#	0.44
	Non-Catholic	84.02	#	#	#
13	National all¹	89.11	1.78	1.51	0.31
	National public	89.25	1.91	0.96	0.33
	Northeast public	85.20	1.48	1.52	0.48
	Midwest public	89.47	2.08	0.65	0.37
	South public	90.43	1.57	0.55	0.30
	West public	89.36	2.61	1.61	0.27
	National private	85.77	0.29	#	#
	Catholic	85.77	0.73	#	#
	Non-Catholic	85.76	#	#	#
¹Includes national public, national private, Bureau of Indian Education			, and Department of Defense Educa	tion Activity schools located in the Un	ited States.

NOTE: National public includes students from public schools only. It includes charter schools, but excludes Bureau of Indian Education schools and Department of Defense Education Activity schools. It is used when comparing national data to those of states, urban districts, or regions. SD = students with disabilities; EL = English learners.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Mathematics Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_response_and_exclusion_rates_for_the_2022_long_term_trend_mathematics_assessment.aspx

NAEP Technical Documentation Student Response and Exclusion Rates for the 2022 Long-Term Trend Reading Assessment

The following table presents the weighted student response, exclusion, and full-time remote rates for the 2022 ages 9 and 13 long-term-trend reading assessments. The exclusion rates give the percentage excluded, among all eligible (i.e., assessed, absent, or excluded) students. Excluded students must be either students with disabilities (SD) or English learners (EL). The response rates indicate the percentage of students assessed among those who it was intended would take the assessment from within the participating schools. Thus, students who were excluded are not included in the denominators of the response rates. The weighted student full-time remote rate indicates the percentage of the student population that is full-time remote (enrolled in brick-and-mortar schools but do not attend school in person).

Weighted student response, exclusion, and full-time remote rates, long-term trend public and private schools, national reading assessment, by age, school type, and census region: 2022

	Weighted student		Weighted percentage of all eligible students	Weighted percentage of all eligible students
	School type and	response rates	Weighted percentage of all eligible students	Weighted percentage of all eligible students	Weighted student full-time remote rates (percent)
Age	census region	(percent)	who are SD and excluded	who are EL and excluded	Weighted student full-time remote rates (percent)
9	National all¹	87.13	1.82	0.90	0.87
	National public	87.00	1.96	0.97	0.94
	Northeast public	82.18	1.35	0.67	0.98
	Midwest public	89.63	0.93	0.53	0.52
	South public	87.84	2.26	0.95	1.17
	West public	86.82	2.74	1.60	0.87
	National private	90.89	0.21	0.01	0.09
	Catholic	92.30	0.57	0.02	0.23
	Non-Catholic	87.70	#	#	#
13	National all¹	89.22	2.44	1.05	0.26
	National public	89.28	2.64	1.09	0.28
	Northeast public	84.05	3.32	2.08	0.25
	Midwest public	89.51	1.59	0.43	0.34
	South public	91.24	2.61	0.80	0.24
	West public	88.66	3.22	1.60	0.34
	National private	87.68	0.17	0.50	#
	Catholic	87.16	0.42	#	#
	Non-Catholic	89.97	#	0.83	#
¹Includes national public, national private, Bureau of India			n Education, and Department of Def	ense Education Activity schools	located in the United States.

NOTE: National public includes students from public schools only. It includes charter schools, but excludes Bureau of Indian Education schools and Department of Defense Education Activity schools. It is used when comparing national data to those of states, urban districts, or regions. SD = students with disabilities; EL = English learners.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_response_and_exclusion_rates_for_the_2022_long_term_trend_reading_assessment.aspx

NAEP Technical Documentation Selection of Primary Sampling Units (PSUs) for the 2022 Assessment

The first stage of sampling for the 2022 assessment was the selection of primary sampling units (PSUs). A PSU is a geographic area comprising an individual county or a group of contiguous counties. One set of 105 PSUs was selected for the 2020 long-term

trend (LTT) assessments. The same set of PSUs used for the 2020 assessments was used for the 2022 LTT assessments.

The PSU samples were drawn using a stratified sample design with one PSU selected per stratum or stratum pair with probability proportional to population size. The size measure used for PSU sampling was persons 17 years of age and younger from 2017 U.S. Census Bureau population estimates.

The PSU sampling frame was constructed by partitioning all counties in the entire United States (the 50 states and the District of Columbia) into 1,001 non-overlapping PSUs as follows:

Each metropolitan statistical area (metro area) was considered a separate PSU, unless it crossed census region boundaries. When this happened, the part within each region was made a separate PSU; and

PSU Generation: Metropolitan Statistical Areas

PSU Generation: Certainty PSUs

PSU Generation: Non- Metropolitan Statistical Areas

PSU Frame Stratification Final PSU Samples

Non-metro area PSUs were constructed from contiguous non-metro area counties within the same state that had minimum populations of 15,000 youths in the Northeast and South census regions and 10,000 youths in the Midwest and West census regions.

Measures of size for constructing the PSUs were based on youth population data obtained from the 2010 Decennial Census summary files.

For the LTT PSU sample, 29 PSUs on the PSU sampling frame were included in the sample with certainty (selected with a probability of 1). The certainty PSUs constitute the 29 largest metropolitan areas in the United States, and for any national sample to be fully representative it is important to include some schools from each of them.

The remaining PSUs were grouped into noncertainty PSU sampling strata within eight primary strata, which were defined by census region and metropolitan status. The stratification of PSUs within the eight primary strata was based on characteristics shown to be highly correlated with student performance such as race/ethnicity composition, income, education, renter status, and percentage of female-headed households. These data were obtained at the county level from the 2006–2010 American Community Survey (ACS) and then aggregated to the PSU level. Seventy-six noncertainty PSU strata were formed. These PSU strata were then paired to form 38 stratum pairs.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/selection_of_primary_sampling_units_psus_for_the_2022_assessment.aspx

Shape92

NAEP Technical Documentation Final Primary Sampling Unit (PSU) Samples for the 2022 Assessment

There was one primary sampling unit (PSU) sample for the 2022 Long Term Trend (LTT) assessment, consisting of 105 sample PSUs of which 29 were certainty and 76 were noncertainty. These are the same sampled PSUs used for the 2020 LTT assessment. Using the same PSU sample was necessary in order to maximize overlap between the 2022 LTT school sample and the 2020 LTT school sample.

To select the noncertainty PSUs for the LTT assessments, one PSU was selected from each of the 76 noncertainty strata defined in Final Primary Sampling Unit Strata. Each PSU was selected with probability proportionate to size, where the size measure was the number of persons 17 years of age and younger from the 2017 Census Bureau population estimates.

In addition, to reduce the burden of any particular school when selecting the 2020 sample PSUs, efforts were made to minimize overlap with the 2013, 2014, 2015, 2016, and 2018 PSU samples. This overlap control was facilitated through the careful assignment of the random starts used to select the noncertainty PSUs. There was a small PSU sample that included 32 noncertainty PSUs in 2017, with which overlap control was not attempted. There was no PSU sample for NAEP 2019.

The table below shows the distribution of the 2022 sample PSUs for each assessment by metropolitan status (metropolitan/non-metropolitan), census region, and certainty/metropolitan status.

Distribution of sampled primary sampling units (PSUs) for the long-term trend (LTT) assessments, by metropolitan status, census region, and certainty/metropolitan status: 2022

Metropolitan status, census region, or certainty/metropolitan status	Number of sampled PSUs for long-term trend
Total	105
Metropolitan status
Metropolitan	85
Non-metropolitan	20
Census region
Northeast	13
Midwest	23
South	41
West	28
Certainty/metropolitan status
Certainty	29
Non-certainty metropolitan	56
Non-certainty non-metropolitan	20
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/final_primary_sampling_unit_samples_for_the_2022_assessment.aspx

NAEP Technical Documentation Primary Sampling Unit (PSU) Frame Stratification for the 2022 Assessment

The primary sampling unit (PSU) strata were determined by census region and metropolitan status (metropolitan or non- metropolitan) for a total of eight "primary" strata. Measures of size were defined for each of these strata, determined by the relative share of the eventual PSU sample (the sample size is designed to be proportional to the number of youths). The PSU stratum measure of size then is the total number of youths (persons 17 years of age and younger) in the stratum. The table below presents these counts for each of the eight primary strata. The relative share of the PSU sample size for each stratum is the number of youths in the stratum divided by the total number of youths, multiplied by 76 (the total

Stepwise Regression Analysis Results for PSU Stratification

Final PSU Strata

number of noncertainty PSU strata). This is shown in the column entitled "Target number of final PSU strata" in the table below. The resulting number is then rounded to the nearest even integer (the integer needs to be even to facilitate variance estimation). Some manual tweaking to the rounding is needed such that the total number of final PSU strata sums to 76. The results of these calculations are given in the table below.

Noncertainty primary sampling unit frame size statistics, by primary stratum: 2022

Primary stratum	PSUs	Counties	Youths	Target number of final PSU strata	Set number of final PSU strata	Youths per final PSU stratum
Total noncertainty PSUs	972	2,901	41,150,742	76	76	541,457
Northeast region metropolitan	43	84	4,353,475	8.0	8	544,184
Northeast region non- metropolitan	48	94	1,021,897	1.9	2	510,949
Midwest region metropolitan	91	229	6,989,571	12.9	12	582,464
Midwest region non- metropolitan	228	762	3,388,214	6.3	6	564,702
South region metropolitan	141	453	13,175,373	24.3	24	548,974
South region non-metropolitan	250	871	5,011,123	9.3	8	626,390
West region metropolitan	68	92	5,553,507	10.3	12	462,792
West region non-metropolitan	103	316	1,657,582	3.1	4	414,396
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

The division of the primary strata into the final strata was done on a stratum-by-stratum basis. The criteria for good PSU strata were 1) the strata should have as nearly equal measures of size as possible (to reduce sampling variance), and 2) the strata should be as heterogeneous in measured achievement as possible (i.e., there should be strata with low mean achievement, strata with mid-level mean achievement, and strata with high mean achievement). This second criterion will also ultimately reduce the variance of the assessment estimates since the final PSU sample will be balanced in terms of assessment means.

PSU assessment means from the current year cannot be used as assessments are only conducted after sampling is completed. Information is available about PSU sociodemographic characteristics in advance, however. An analysis was done within each primary stratum to find sociodemographic variables that were good predictors of performance on the eighth-grade reading assessments conducted in five previous NAEP cycles (2002, 2003, 2005, 2007, and 2009). Using these sociodemographic variables to define final strata should increase the chance of having efficient stratum definitions. Stepwise Regression Analysis Results for PSU Stratification describes this analysis for each primary stratum.

The final step in stratification was to define the desired number of final strata using the selected stratifiers, while constructing final strata that were as close to equal size as possible (with size defined by number of youth). The objective was to establish final strata that had a high between-stratum variance for the stratifiers (i.e., which "spread out" the stratifiers as much as possible). These strata are given in Final PSU Strata.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/primary_sampling_unit_frame_stratification_for_the_2022_assessment.aspx

Shape94

NAEP Technical Documentation Final Primary Sampling Unit (PSU) Strata for the 2022 Assessment

The strata were defined using the selected stratifiers from the stepwise regression analysis (see Stepwise Regression Analysis Results for PSU Stratification). The cutoffs were selected so that roughly equal measures of size were represented by each stratum.

The number of stratifiers used to define the noncertainty PSU strata within each primary stratum ranged from 1 to 5 stratifiers depending on the size of the primary stratum. For instance, the Northeast non-metropolitan primary stratum, which had about 1 million youths in noncertainty PSUs, used only one stratifier; whereas the South metropolitan primary stratum had about 13 million youths in noncertainty PSUs and used five stratifiers.

The final noncertainty PSU strata are presented in summary tables for each primary PSU stratum. The tables show the definition, number of PSUs, and size of each stratum.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/final_primary_sampling_unit_strata_for_the_2022_assessment.aspx

Stratification for Northeast metropolitan noncertainty primary sampling units

Stratification for Northeast non-metropolitan noncertainty primary sampling units

Stratification for Midwest metropolitan noncertainty primary sampling units

Stratification for Midwest non-metropolitan noncertainty primary sampling units

Stratification for South metropolitan noncertainty primary sampling units

Stratification for South non-metropolitan

noncertainty primary sampling units

Stratification for West metropolitan noncertainty primary sampling units

NAEP Technical Documentation Stratification for Midwest

Metropolitan Noncertainty Primary Sampling Units

Stratification for West non-metropolitan noncertainty primary sampling units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the Midwest metropolitan primary stratum. Columns 2 through 5 show the characteristics used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for Midwest metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	Tertiary stratifier	Quaternary stratifier	PSUs	Measure of size
Total	†	†	†	†	91	6,989,571
1	Percentage of female-headed households <= 9.6	Percentage of female-headed households <= 8.4	†	†	14	613,052
2	Percentage of female-headed households <= 9.6	Percentage of female-headed households > 8.4	†	†	15	599,573
3	Percentage of female-headed households > 9.6	Percentage of renters <= 30.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 14.2	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 10.1	14	548,336
4	Percentage of female-headed households > 9.6	Percentage of renters <= 30.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 14.2	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 10.1	10	567,571
5	Percentage of female-headed households > 9.6	Percentage of renters <= 30.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 14.2	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 17.6	8	548,156
6	Percentage of female-headed households > 9.6	Percentage of renters <= 30.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 14.2	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 17.6	11	552,422
7	Percentage of female-headed households > 9.6	Percentage of renters (30.6-32.2]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 16.6	Percentage of female-headed households <= 12.1	6	562,849
8	Percentage of female-headed households > 9.6	Percentage of renters (30.6-32.2]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 16.6	Percentage of female-headed households > 12.1	3	576,197
9	Percentage of female-headed households > 9.6	Percentage of renters (30.6-32.2]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 16.6	Percentage of renters <= 31.8	2	639,144
10	Percentage of female-headed households > 9.6	Percentage of renters (30.6-32.2]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 16.6	Percentage of renters > 31.8	2	582,152
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Stratum Primary stratifier Secondary stratifier Tertiary stratifier Quaternary stratifier PSUs

Measure of

size

Percentage of female-headed households > 9.6

Percentage of renters > 32.2

Percentage of female-headed households

<= 12.2

†

649,462

Percentage of female-headed households > 9.6

Percentage of renters > 32.2

Percentage of female-headed households

> 12.2

†

550,657

Mean

†

582,464

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_midwest_metropolitan_noncertainty_primary_sampling_units.aspx

Shape95

NAEP Technical Documentation Stratification for Midwest Non-Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the Midwest non-metropolitan primary stratum. Columns 2 and 3 show the primary and secondary characteristics used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for Midwest non-metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	PSUs	Measure of size
Total	†	†	228	3,388,214
1	Percentage of children below the poverty line <= 16.1	Percentage of children below the poverty line <= 13.7	41	573,682
2	Percentage of children below the poverty line <= 16.1	Percentage of children below the poverty line > 13.7	36	580,649
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Stratum Primary stratifier Secondary stratifier PSUs

Measure of

size

3	Percentage of children below the poverty line (16.1-20.7]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 5.4	38	556,318
4	Percentage of children below the poverty line (16.1-20.7]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 5.4	37	560,613
5	Percentage of children below the poverty line > 20.7	Percentage of children below the poverty line <= 24	38	553,089
6	Percentage of children below the poverty line > 20.7	Percentage of children below the poverty line > 24	38	563,863
Mean	†	†	†	564,702

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_midwest_nonmetropolitan_noncertainty_primary_sampling_units.aspx

Shape96

NAEP Technical Documentation Stratification for Northeast Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the Northeast metropolitan primary stratum. Columns 2 and 3 show the primary and secondary characteristics, respectively, used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for Northeast metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	PSUs	Measure of size
Total	†	†	43	4,353,475
1	Percentage of female-headed households <= 11	Percentage of female-headed households <= 10.3	10	526,409
2	Percentage of female-headed households <= 11	Percentage of female-headed households > 10.3	7	600,293
3	Percentage of female-headed households (11-11.6]	Percentage of persons aged 25+ who completed high school <= 89.7	7	545,323
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Stratum Primary stratifier Secondary stratifier PSUs Measure of size

4	Percentage of female-headed households (11-11.6]	Percentage of persons aged 25+ who completed high school > 89.7	3	518,431
5	Percentage of female-headed households (11.6- 12.7]	Percentage of female-headed households <= 12.5	5	580,767
6	Percentage of female-headed households (11.6- 12.7]	Percentage of female-headed households > 12.5	3	521,663
7	Percentage of female-headed households > 12.7	Percentage of female-headed households <= 13.5	2	554,582
8	Percentage of female-headed households > 12.7	Percentage of female-headed households > 13.5	6	506,007
Mean	†	†	†	544,184

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_northeast_metropolitan_noncertainty_primary_sampling_units.aspx

Shape97

NAEP Technical Documentation Stratification for Northeast Non-Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the Northeast non-metropolitan primary stratum. Column 2 shows the primary characteristic used to define the strata along with the cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for Northeast non-metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	PSUs	Measure of size
Total	†	48	1,021,897
1	Percentage of persons aged 25+ with a college degree <= 19.1	23	505,650
2	Percentage of persons aged 25+ with a college degree > 19.1	25	516,247
Mean	†	†	510,949
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_northeast_nonmetropolitan_noncertainty_primary_sampling_units.aspx

NAEP Technical Documentation Stratification for South Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the South metropolitan primary stratum. Columns 2 through 6 show the characteristics used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for South metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	Tertiary stratifier	Quaternary stratifier	Quinary stratifier	PSUs	Measure of size
Total	†	†	†	†	†	141	13,175,373
1	Percentage of female-headed households <= 16.9	Percentage of renters <= 33.5	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2	Per capita household income <= $23,025	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 14.9	14	533,826
2	Percentage of female-headed households <= 16.9	Percentage of renters <= 33.5	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2	Per capita household income <= $23,025	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 14.9	12	509,782
3	Percentage of female-headed households <= 16.9	Percentage of renters <= 33.5	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2	Per capita household income ($23,025-$25,326]	Percentage of female- headed households <= 12.1	6	539,598
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Primary

Secondary

Measure of

Stratum

stratifier

Tertiary stratifier

Quaternary stratifier

Quinary stratifier

PSUs

size

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2

Per capita household income

($23,025-$25,326]

Percentage of female- headed households >

12.1

543,970

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2

Per capita household income

($25,326-$27,540]

Percentage of female- headed households <= 11.8

456,746

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2

Per capita household income

($25,326-$27,540]

Percentage of female- headed households >

11.8

652,881

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2

Per capita household income

($27,540-$28,621]

†

575,617

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 28.2

Per capita household income

> $28,621

†

535,472

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (28.2-30.6]

Percentage of female-headed

households <= 13

†

564,610

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (28.2-30.6]

Percentage of female-headed

households > 13

†

545,366

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Primary

Secondary

Measure of

Stratum

stratifier

Tertiary stratifier

Quaternary stratifier

Quinary stratifier

PSUs

size

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (30.6-33.2]

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 32.2

†

574,325

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (30.6-33.2]

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 32.2

†

544,937

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific

Islander youth > 33.2

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 36.9

†

531,652

Percentage of female-headed households <=

16.9

Percentage of renters <=

33.5

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific

Islander youth > 33.2

Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 36.9

†

533,107

Percentage of female-headed households <=

16.9

Percentage of renters > 33.5

Per capita household income

<= $23,655

Percentage of renters <= 36.9

†

566,668

Percentage of female-headed households <=

16.9

Percentage of renters > 33.5

Per capita household income

<= $23,655

Percentage of renters >

36.9

†

558,330

Percentage of female-headed households <=

16.9

Percentage of renters > 33.5

Per capita household income

($23,655-$26,682]

Percentage of female-headed

households <= 14.2

†

576,105

Percentage of female-headed households <=

16.9

Percentage of renters > 33.5

Per capita household income

($23,655-$26,682]

Percentage of female-headed

households > 14.2

†

566,865

Percentage of female-headed

Percentage of renters > 33.5

Per capita household income >

$26,682

Percentage of renters <= 38.7

†

540,457

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Primary

Stratum stratifier

Secondary

stratifier

Tertiary stratifier

Quaternary stratifier

Quinary stratifier

PSUs

Measure of

size

households <=

16.9

Shape99

Percentage of female-headed households <=

16.9

Percentage of renters > 33.5

Per capita household income >

$26,682

Percentage of renters >

38.7

† 2 608,592

Percentage of female-headed households >

16.9

Percentage of female-headed households >

16.9

Per capita household income <=

$21,548

Per capita household income <=

$21,548

Percentage of renters <= 31.7 † † 4 560,596

Percentage of renters > 31.7 † † 9 549,613

Percentage of female-headed households >

16.9

Percentage of female-headed households >

16.9

Per capita household income >

$21,548

Per capita household income >

$21,548

Percentage of female-headed

households <= 18.7

Percentage of female-headed

households > 18.7

† † 5 501,582

† † 3 504,676

Mean † † † † † † 548,974

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_south_metropolitan_noncertainty_primary_sampling_units.aspx

Shape100

NAEP Technical Documentation Stratification for South Non-Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the South non-metropolitan primary stratum. Columns 2 through 4 show the characteristics used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for South non-metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	Tertiary stratifier	PSUs	Measure of size
Total	†	†	†	250	5,011,123
1	Percentage of female-headed households <= 12.6	Per capita household income <= $20,111	Percentage of female- headed households <= 11.3	33	633,594
2	Percentage of female-headed households <= 12.6	Per capita household income <= $20,111	Percentage of female- headed households > 11.3	33	627,232
3	Percentage of female-headed households <= 12.6	Per capita household income ($20,111-$22,659]	†	32	645,084
4	Percentage of female-headed households <= 12.6	Per capita household income > $22,659	†	28	647,245
5	Percentage of female-headed households (12.6-16.2]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 29.2	†	32	622,008
6	Percentage of female-headed households (12.6-16.2]	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 29.2	†	32	633,149
7	Percentage of female-headed households > 16.2	Per capita household income <= $17,691	†	31	595,547
8	Percentage of female-headed households > 16.2	Per capita household income > $17,691	†	29	607,264
Mean	†	†	†	†	626,390
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_south_nonmetropolitan_noncertainty_primary_sampling_units.aspx

NAEP Technical Documentation Stratification for West Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the West metropolitan primary stratum. Columns 2 through 4 show the characteristics used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (persons 17 years of age and younger).

Stratification for West metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	Tertiary stratifier	PSUs	Measure of size
Total	†	†	†	68	5,553,507
1	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 18.4	Percentage of renters <= 29.3	†	8	447,020
2	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 18.4	Percentage of renters (29.3-31]	†	6	500,321
3	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 18.4	Percentage of renters > 31	Percentage of persons aged 25+ with a college degree <= 28.1	10	447,141
4	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 18.4	Percentage of renters > 31	Percentage of persons aged 25+ with a college degree > 28.1	9	454,153
5	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (18.4-44.3]	Percentage of renters <= 33.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 21	2	519,462
6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (18.4-44.3]	Percentage of renters <= 33.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 21	5	429,036
7	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (18.4-44.3]	Percentage of renters > 33.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 32.4	7	466,560
8	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (18.4-44.3]	Percentage of renters > 33.6	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 32.4	5	474,872
9	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (44.3-54.4]	Percentage of renters <= 37.9	†	4	454,868
10	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth (44.3-54.4]	Percentage of renters > 37.9	†	2	462,254
11	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 54.4	Percentage of persons aged 25+ with a college degree <= 15.1	†	7	447,696
12	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other	Percentage of persons aged 25+ with a college	†	3	450,124
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Stratum Primary stratifier Secondary stratifier Tertiary stratifier PSUs

Measure of

size

Mean

cific Islander youth > 54.4

†

degree > 15.1

†

462,792

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_west_metropolitan_noncertainty_primary_sampling_units.aspx

NAEP Technical Documentation Stratification for West Non-Metropolitan Noncertainty Primary Sampling Units

The following table provides the definition, number of PSUs, and size of each noncertainty PSU stratum in the West non-metropolitan primary stratum. Columns 2 and 3 show the primary and secondary characteristics, respectively, used to define the strata along with their respective cutoffs. The size of each stratum is given in the last column and is in terms of the number of youths (person 17 years of age and younger).

Stratification for West non-metropolitan noncertainty primary sampling units (PSUs), by stratum: 2022

Stratum	Primary stratifier	Secondary stratifier	PSUs	Measure of size
Total	†	†	103	1,657,582
1	Percentage of female-headed households <= 9.7	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth <= 12	27	422,853
2	Percentage of female-headed households <= 9.7	Percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander youth > 12	28	403,074
3	Percentage of female-headed households > 9.7	Percentage of female-headed households <= 11.9	26	414,689
4	Percentage of female-headed households > 9.7	Percentage of female-headed households > 11.9	22	416,966
Mean	†	†	†	414,396
† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_for_west_nonmetropolitan_noncertainty_primary_sampling_units.aspx

NAEP Technical Documentation Stepwise Regression Analysis Results for Primary Sampling Unit (PSU) Stratification for the 2022 Assessment

The objective was to find the optimum set of primary sampling unit (PSU)-level sociodemographic characteristics in terms of strength of relationship to achievement. The PSU- level values of these characteristics were derived from the 2010 Decennial Census summary files and the 2006–2010 American Community Survey (ACS) estimates, computed by combining the county-level data (using county youth estimates as the relative weighting factor for each county within the PSU). The characteristics used were as follows:

aggregate race/ethnicity percentages (percentage of Black, Hispanic, American Indian/Alaska Native, or Native Hawaiian/Other Pacific Islander students); income levels (per capita household income, percentage of children below the poverty line);

education levels in the population (i.e., percentage of persons aged 25+ who completed high school, percentage of persons aged 25+ with a college degree); percentage of renters (i.e., percentage of householders who rent rather than own their place of residence); and

percentage of female-headed households.

These PSU-level census characteristics were analyzed with the eighth-grade reading assessment scores from five previous NAEP cycles (2002, 2003, 2005, 2007, and 2009). The criterion was that good strata should be heterogeneous for each of the five characteristics (i.e., within-stratum variance for each assessment value should be low and between-stratum variance high).

The analysis was done separately within each of the eight primary strata (census region and metropolitan status), using a forward stepwise regression approach, with a p- value of .20. The results of the regression model were used to generate the Final PSU Strata.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stepwise_regression_analysis_results_for_primary_sampling_unit_stratification_for_the_2022_assessment.aspx

NAEP Technical Documentation Primary Sampling Unit (PSU) Generation: Certainty PSUs for the 2022 Assessment

Any primary sampling unit (PSU) was defined as a certainty PSU if it had 500,000 or more youths or if it represented more than 80 percent of its assigned stratum. The estimated number of youths used to designate certainty PSUs was the number of persons aged 17 or under from the 2010 Decennial Census. These PSUs were so large that a sample of schools was taken from all of them (rather than from only a subsample of them, as with noncertainty PSUs). The Honolulu, Hawaii PSU was included as certainty by

design in order to reduce the variances of estimates for Asian and Native Hawaiian/Other Pacific Islander students. A total of 29 PSUs were classified as certainties in the

PSU frame. The table below provides a listing of the certainty PSUs by census region. Note that the names of the metropolitan statistical areas do not represent the cities proper. Rather they can and do cross jurisdiction and county boundaries (for example, the Boston-Cambridge-Quincy metropolitan statistical area includes Massachusetts and New Hampshire). The "Number of youths" column in the table reflects updated 2017 U.S. Census Bureau population estimates.

Metropolitan statistical area definitions for certainty PSUs, by census region: 2022

Census region/Metropolitan statistical area	Jurisdiction	Number of counties	Number of youths
Total	†	241	32,504,636
Northeast	†	39	6,372,003
Boston-Cambridge-Quincy	MA-NH	7	964,952
New York-Northern New Jersey-Long Island	NY-NJ-PA	23	4,222,175
Philadelphia-Camden-Wilmington (Northeast part)	PA-NJ	9	1,184,876
Midwest	†	64	5,149,811
Chicago-Joliet-Naperville	IL-IN-WI	14	2,192,226
Detroit-Warren-Livonia	MI	6	960,673
Kansas City	MO-KS	15	526,178
Minneapolis-St. Paul-Bloomington	MN-WI	13	838,824
St. Louis	MO-IL	16	631,910
South	†	98	10,318,929
Atlanta-Sandy Springs-Marietta	GA	28	1,451,162
Baltimore-Towson	MD	7	616,336
Dallas-Fort Worth-Arlington	TX	12	1,926,790
Houston-Sugar Land-Baytown	TX	10	1,850,453
Miami-Fort Lauderdale-Pompano Beach	FL	3	1,252,616
Orlando-Kissimmee-Sanford	FL	4	553,844
San Antonio-New Braunfels	TX	8	629,757
Tampa-St. Petersburg-Clearwater	FL	4	623,162
Washington-Arlington-Alexandria	DC-VA-MD-WV	22	1,414,809
West	†	40	10,663,893
Denver-Aurora-Broomfield	CO	10	659,646
Honolulu	HI	1	209,809
Las Vegas-Paradise	NV	1	514,192
Los Angeles-Long Beach-Santa Ana	CA	2	2,930,904
Phoenix-Mesa-Glendale	AZ	2	1,144,270
Portland-Vancouver-Hillsboro	OR-WA	7	533,626
Riverside-San Bernardino-Ontario	CA	2	1,187,880

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Census region/Metropolitan statistical area Jurisdiction Number of counties Number of youths

Sacramento--Arden-Arcade--Roseville	CA	4	534,664
San Diego-Carlsbad-San Marcos	CA	1	728,528
San Francisco-Oakland-Fremont	CA	5	938,267
San Jose-Sunnyvale-Santa Clara	CA	2	445,589
Seattle-Tacoma-Bellevue	WA	3	836,518

† Not applicable.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/primary_sampling_unit_generation_certainty_psus_for_the_2022_assessment.aspx

NAEP TechnicaL Documentation Primary Sampling Unit (PSU) Generation: Metropolitan Statistical Areas for the 2022 Assessment

Primary Sampling Units (PSUs) for NAEP are classified as either metropolitan statistical areas¹(metro areas) or non-metro areas. Each metro area constitutes a separate PSU, except when it crosses census region boundaries. Such metro areas are split along regional boundaries with each regional part considered its own distinct PSU. For example, the Louisville-Jefferson County, KY-IN metro area was partitioned into two PSUs, one for the counties in Kentucky which are part of the South region and the other for counties in Indiana which are part of the Midwest region.

In total, there were 372 metro area PSUs, 29 of which were defined as certainty PSUs. The remaining 343 metro area PSUs, covering a total of 858 counties, constituted the noncertainty portion of the metro area PSU sampling frame. The estimated number of youths used to define certainty and noncertainty PSUs was the number of persons aged 17 or under from the 2010 Decennial Census. The table below presents the number of PSUs, the number of counties represented, and the updated estimated number of youths (total and mean per PSU) in noncertainty metro area PSUs by census region. These updated estimates come from the county-level estimates of numbers of persons aged 0 to 17 from the 2017 U.S. Census Bureau population estimates.

Noncertainty metropolitan primary sampling unit (PSU) frame, by census region: 2022

Census region	PSUs	Counties	Youths	Mean number of youths per PSU
Total	343	858	30,071,926	87,673
Northeast	43	84	4,353,475	101,244
Midwest	91	229	6,989,571	76,808
South	141	453	13,175,373	93,442
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

West

5,553,507

81,669

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

¹Based on the 2009 metro area definitions, the most recent available metro area definitions at the time of PSU construction, from the U.S. Office of Management and Budget (OMB Bulletin No. 10-02).

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/primary_sampling_unit_generation_metropolitan_statistical_areas_for_the_2022_assessment.aspx

NAEP Technical Documentation Primary Sampling Unit (PSU) Generation: Non- Metropolitan Statistical Areas for the 2022 Assessment

Primary Sampling Units (PSUs) for NAEP are classified as either metropolitan statistical areas¹(metro areas) or non-metro areas. Non-metro area PSUs are PSUs that are made up of counties that are not part of any metropolitan statistical areas.

An algorithm was used to define a preliminary set of non-metro area PSUs satisfying specific design constraints. The algorithm attempted to form PSUs that were geographically compact, of a minimum population size based on 2010 Decennial Census estimates (15,000 youths in the Northeast and South census regions, and 10,000 youths in the Midwest and West census regions) and that also did not cross state boundaries. The input set consisted of all non-metro area counties. The county which had the largest maximum point-to-point distance was addressed first. It was grouped with adjacent non-metro area counties until the minimum PSU size was met. The algorithm was then run on the remaining non-metro area counties not yet assigned to a PSU to combine the county with the largest maximum point-to-point distance among the remaining counties with its adjacent non-metro area counties until the minimum PSU size was met. This process was repeated until all counties were grouped into PSUs.

When the algorithm was unable to create PSUs that conformed to the specific design constraints, manual adjustments were made. The end result of this procedure was that all non-metro area PSUs were contained within state boundaries, but in some cases the PSU size fell slightly below the pre-specified minimum.

In total, there were 629 non-metro area PSUs covering a total of 2,043 counties, all of which constitute the non-metro area PSU sampling frame. The table below presents the number of PSUs, the number of counties represented, and the updated estimated number of youths (total and mean per PSU) in the non-metro area PSU sampling frame by census region. The updated estimated number of youths (persons aged 0 to 17) for each county comes from the 2017 U.S. Census Bureau population estimates.

Non-metropolitan statistical area primary sampling unit (PSU) frame, by census region: 2022

Census region	PSUs	Counties	Youths	Mean number of youths per PSU
Total	629	2,043	11,078,816	17,613
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

Northeast	48	94	1,021,897	21,290
Midwest	228	762	3,388,214	14,861
South	250	871	5,011,123	20,044
West	103	316	1,657,582	16,093

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Long-Term Trend Assessment.

¹Based on the 2009 metro area definitions, the most recent available metro area definitions at the time of PSU construction, from the U.S. Office of Management and Budget (OMB Bulletin No. 10-02).

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/primary_sampling_unit_generation_non_metropolitan_statistical_areas_for_the_2022_assessment.aspx

NAEP Technical Documentation Sample Design for the 2022 State Assessment

The NAEP 2022 state assessment sampled jurisdictions comprising the 50 states, the District of Columbia, Puerto Rico, Bureau of Indian Education (BIE) schools, Department of Defense Education Activity (DoDEA) schools, and school districts participating in the Trial Urban District Assessment (TUDA). Each sample, with the exception of BIE schools, was designed to produce aggregate estimates with approximately equal precision for all the participating jurisdictions, as well as estimates for various student populations of interest. In 2022, by design BIE was not a reportable jurisdiction. However, to ensure that there were sufficient numbers of American Indian

or Alaska Native (AI/AN) students at the national level, a small number of BIE schools were included in the sample.

The target population for the NAEP 2022 state assessments covered fourth- and eighth-grade students in public schools who were enrolled in grades 4 and 8 at the time of assessment. Operational mathematics and reading assessments were conducted in all jurisdictions, including the TUDA districts, with the exception of Puerto Rico, where only the operational mathematics assessment was conducted.

The state samples were selected to have maximum overlap with the school samples for the NAEP 2021 Monthly School Survey and the NAEP 2021 School and Teacher Questionnaire Study. This overlap control was achieved for these samples by using an adaptation of the Keyfitz process.

Target Population Sampling Frame Stratification of Schools School Sample Selection Ineligible Schools Student Sample Selection

School and Student Participation

The overall target student sample size for the operational samples in each non-TUDA jurisdiction, with the exception of Puerto Rico, was 4,100 at grade 4 and 4,200 at grade 8. The goal at each grade was to obtain 3,500 assessed students after attrition: 1,750 for mathematics and 1,750 for reading. For the operational mathematics assessment in Puerto Rico, the target student sample size was 3,600 for both grades, with the goal of assessing 3,000 students after attrition.

The primary sampling frame for each grade included public schools having the relevant grade in each jurisdiction. The samples were selected based on a two-stage sample design:

selection of schools within participating jurisdictions; and selection of students within schools.

The first-stage samples of schools were selected with probability proportional to a measure of size based on the estimated grade-specific enrollment in the schools.

The sampling of students at the second stage involved two steps: (1) sampling of students in the targeted grade (fourth or eighth) from each sampled school, and (2) assignment of assessment subject (mathematics or reading) to the sampled students.

For the TUDA samples, schools were sampled from the 26 participating TUDA districts at the same time schools were selected for the non-TUDA jurisdiction samples. The participating TUDA districts are listed below:

Albuquerque Public Schools, New Mexico; Atlanta Public Schools, Georgia;

Austin Independent School District, Texas; Baltimore City Public Schools, Maryland; Boston Public Schools, Massachusetts;

Charlotte-Mecklenburg Schools, North Carolina; Chicago Public Schools, Illinois;

Clark County School District, Nevada;

Cleveland Metropolitan School District, Ohio; Dallas Independent School District, Texas;

Denver Public Schools, Colorado; Detroit Public Schools, Michigan;

District of Columbia Public Schools, District of Columbia; Duval County Public Schools, Florida;

Fort Worth Independent School District, Texas; Guilford County Schools, North Carolina;

Hillsborough County Public Schools, Florida; Houston Independent School District, Texas; Jefferson County Public Schools, Kentucky;

Los Angeles Unified School District, California; Miami-Dade County Public Schools, Florida;

Milwaukee Public Schools, Wisconsin;

New York City Department of Education, New York; San Diego Unified School District, California;

School District of Philadelphia, Pennsylvania; and Shelby County Schools, Tennessee.

These subsamples affected the design of the state samples in those states where TUDA districts were oversampled. In each of these states, there were distinct sampling rates for each TUDA district and for the balance of the state (i.e., the rest of the state not in a TUDA district). For the six large TUDA districts (i.e., New York, Los Angeles, Chicago, Miami-Dade, Clark County, and Houston) the target assessed student sample size for the operational samples was three-quarters the size of the non-TUDA jurisdictions: 2,625 per grade (i.e., 1,313 per subject for each grade). For the remaining TUDA districts, the target assessed student sample size for the operational samples was half the size of the state sample: 1,750 per grade (i.e., 875 per subject for each grade).

Each selected school provided a list of eligible enrolled students from which a systematic sample of students was drawn. In fourth- and eighth-grade schools, 50 students, if possible, were selected from each school: roughly 25 for mathematics and 25 for reading. In some very large schools, multiples of 50 students (i.e., 100, 150, etc.) were selected. Details can be found on the student sample selection page.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sample_design_for_the_2022_state_assessment.aspx

Shape127

NAEP Technical Documentation Ineligible Schools for the 2022 State Assessment

The Common Core of Data (CCD)-based sampling frames, from which most of the sampled schools were drawn, corresponds to the 2019–2020 school year, two years prior to the assessment school year. During the intervening period, some of these schools either closed, no longer offered the grade of interest, or were ineligible for other reasons. In such cases, the sampled school was coded as ineligible.

Total and Eligible Schools Sampled Eligibility Status of Schools Sampled

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/ineligible_schools_for_the_2022_state_assessment.aspx

Shape128

NAEP Technical Documentation Eligibility Status of Schools Sampled for the 2022 State Assessment

Sampled schools, state assessment, by grade and eligibility status: 2022

	Grade 4		Grade 8
Eligibility status	Unweighted count of schools	Unweighted percentage	Unweighted count of schools	Unweighted percentage
All sampled public schools	6,010	100.00	5,490	100.00
Eligible	5,830	96.99	5,250	95.70
Ineligible	181	3.01	236	4.30
Has sampled grade, but no eligible students	22	0.37	23	0.42
Does not have sampled grade	48	0.80	59	1.07
NOTE: Numbers of schools are rounded to nearest ten, except those pertaining to ineligible schools. Detail may not sum to totals due to rounding. Percentages are based on unrounded counts.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics and Reading Assessments.

Shape129 Grade 4 Grade 8

Eligibility status

Unweighted count of

schools

Unweighted percentage

Unweighted count of

schools

Unweighted percentage

School closed	51	0.85	51	0.93
Not a regular school	52	0.87	81	1.48
Other ineligible school	8	0.13	22	0.40
Duplicate on sampling frame	0	0	0	0

NOTE: Numbers of schools are rounded to nearest ten, except those pertaining to ineligible schools. Detail may not sum to totals due to rounding. Percentages are based on unrounded counts.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/eligibility_status_of_schools_sampled_for_the_2022_state_assessment.aspx

Shape130

NAEP Technical Documentation Total and Eligible Sampled Schools for the 2022 State Assessment

The following table presents the numbers of total and eligible fourth- and eighth-grade schools sampled for each NAEP 2022 state assessment jurisdiction.

Total and eligible sampled schools, state assessment, by grade and jurisdiction: 2022

Jurisdiction	Grade 4		Grade 8
Jurisdiction
Total school sample	Eligible school sample	Total school sample	Eligible school sample
Total	6,010	5,830	5,490	5,250
Alabama	90	90	90	90
Alaska	130	130	110	100
Arizona	90	90	90	90
Arkansas	90	80	90	90
California–Los Angeles	60	60	60	60
California–San Diego	40	40	40	30
California–Balance	80	80	80	70
Colorado–Denver	40	40	40	40
NOTE: Numbers of schools rounded to nearest ten. Detail may not sum to totals due to rounding.

Colorado–Balance	80	80	80	70
Connecticut	90	80	90	80
Delaware	80	70	50	50
Florida–Duval County	40	40	40	40
Florida–Hillsborough County	40	40	40	40
Florida–Miami-Dade County	60	60	70	60
Florida–Balance	60	60	70	70
Georgia–Atlanta	40	40	30	30
Georgia–Balance	80	80	80	80
Hawaii	90	90	50	50
Idaho	90	90	90	80
Illinois–Chicago	70	70	70	70
Illinois–Balance	80	70	70	70
Indiana	90	90	90	80
Iowa	90	90	90	80
Kansas	100	100	90	90
Kentucky–Jefferson County	40	40	30	20
Kentucky–Balance	70	70	80	70
Louisiana	90	80	90	90
Maine	110	110	90	90
Maryland–Baltimore	50	40	50	40
Maryland–Balance	80	80	80	80
Massachusetts–Boston	50	50	50	40
Massachusetts–Balance	80	80	80	80
Michigan–Detroit	40	40	40	40
Michigan–Balance	90	80	90	90
Minnesota	90	90	100	80
Mississippi	90	90	90	80
Missouri	100	90	100	90
Montana	130	120	100	100
Nebraska	100	100	100	100
Nevada–Clark County	60	60	50	50
Nevada–Balance	30	30	30	30
New Hampshire	100	100	80	80

New Jersey	90	90	90	90
New Mexico–Albuquerque	40	40	40	30
New Mexico–Balance	70	70	70	70
New York–New York City	70	70	70	70
New York–Balance	60	50	60	60
North Carolina–Charlotte	40	40	30	30
North Carolina–Guilford County	40	40	30	20
North Carolina–Balance	80	70	80	70
North Dakota	120	120	90	80
Ohio–Cleveland	50	50	50	50
Ohio–Balance	90	80	90	80
Oklahoma	100	90	90	90
Oregon	90	90	90	90
Pennsylvania–Philadelphia	40	40	40	40
Pennsylvania–Balance	80	80	80	80
Rhode Island	90	90	60	60
South Carolina	90	90	90	90
South Dakota	120	120	100	90
Tennessee–Shelby County	40	40	40	40
Tennessee–Balance	80	80	80	80
Texas–Austin	40	40	20	20
Texas–Dallas	40	40	40	40
Texas–Fort Worth	40	40	30	20
Texas–Houston	60	60	40	40
Texas–Balance	80	80	80	80
Utah	90	80	90	90
Vermont	130	130	90	90
Virginia	90	80	90	80
Washington	90	90	90	90
West Virginia	100	100	90	90
Wisconsin–Milwaukee	50	50	40	40
Wisconsin–Balance	90	80	80	80
Wyoming	100	100	70	60
Other jurisdictions

Bureau of Indian Education (BIE)	10	10	10	10
Department of Defense Education Activity (DoDEA)	100	90	60	50
District of Columbia (TUDA)	50	50	30	20
District of Columbia–Balance	40	30	50	40
Puerto Rico	150	150	150	150

NOTE: Numbers of schools rounded to nearest ten. Detail may not sum to totals due to rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/total_and_eligible_sampled_schools_for_the_2022_state_assessment.aspx

Shape142

NAEP Technical Documentation Sampling Frame for the 2022 State Assessment

The primary sampling frames for the 2022 fourth- and eighth-grade public school samples for the state assessments in mathematics and reading were developed from the Common Core of Data (CCD) file corresponding to the 2019–2020 school year. The CCD file is the Department of Education’s primary database of public elementary and secondary schools in the United States including U.S. territories. It includes all regular public, state-operated public, Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools open during the 2019–2020 school year. These sampling frames are referred to as the CCD-based sampling frames.

Fourth- and Eighth-Grade Schools and Enrollment

New-School Sampling Frame

A secondary set of sampling frames were also created for these fourth- and eighth-grade samples to account for schools that newly opened or became newly eligible between the 2019–2020 and 2021–2022 school years. These frames contain brand-new and newly-eligible fourth- and eighth-grade schools and are referred to as the new-school sampling frames.

Both sets of sampling frames excluded ungraded schools, vocational schools with no enrollment, special-education-only schools, prison and hospital schools, home school entities, virtual or online schools, adult and evening schools, and juvenile correctional institutions. Vocational schools with no enrollment serve students who split their time between the vocational school and their home school.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/sampling_frame_for_the_2022_state_assessment.aspx

Shape154

NAEP Technical Documentation Fourth- and Eighth-Grade Schools and Enrollment in the 2022 State Assessment Sampling Frame

The following table presents the number of fourth- and eighth-grade public schools and their estimated enrollment, as contained in the Common Core of Data (CCD)-based sampling frames, by jurisdiction, for the state mathematics and reading assessments. Grade 4 or grade 8 enrollment was estimated for each school as the average of the per- grade enrollments for grades 1 through 8, counting only the grades in that range that were offered by the school.

Number of schools and enrollment in public school sampling frame, state assessment, by grade and jurisdiction: 2022

	Grade 4		Grade 8
Jurisdiction	Schools	Enrollment	Schools	Enrollment
Total	52,248	3,750,123	29,665	3,870,570
Alabama	689	56,232	436	56,217
Alaska	346	9,155	266	9,202
Arizona	1,230	86,152	830	88,080
Arkansas	474	37,099	304	37,124
California–Los Angeles	497	38,919	126	33,124
California–San Diego	121	8,247	38	7,036
California–Balance	5,517	407,176	2,932	425,888
Colorado–Denver	110	6,823	62	6,571
Colorado–Balance	989	59,308	552	62,168
Connecticut	559	37,280	289	39,376
Delaware	117	10,511	68	11,041
Florida–Duval County	124	10,577	60	9,784
Florida–Hillsborough County	189	17,620	100	16,814
Florida–Miami	287	25,525	190	26,991
Florida–Balance	1,690	161,932	952	166,395
Georgia–Atlanta	56	4,443	26	3,914
Georgia–Balance	1,196	126,156	557	134,401
Hawaii	208	14,325	84	13,911
Idaho	393	23,634	219	24,793
Illinois–Chicago	459	26,029	454	26,680
Illinois–Balance	1,762	113,320	1,144	121,781
Indiana	1,033	77,755	490	80,844
Iowa	614	36,402	357	38,428
Kansas	695	35,714	392	37,025
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Assessment.

Kentucky–Jefferson County	99	7,443	41	7,425
Kentucky–Balance	625	42,954	390	45,001
Louisiana	739	53,725	499	53,361
Maine	309	13,041	198	13,472
Maryland–Baltimore	116	6,420	88	5,373
Maryland–Balance	776	62,293	283	62,434
Massachusetts–Boston	70	3,621	46	3,676
Massachusetts–Balance	881	65,102	446	68,558
Michigan–Detroit	72	4,164	59	3,362
Michigan–Balance	1,605	100,469	1,043	107,587
Minnesota	990	65,135	730	67,317
Mississippi	407	35,543	278	36,803
Missouri	1,163	67,268	712	70,194
Montana	394	11,721	277	11,939
Nebraska	511	23,867	290	23,444
Nevada–Clark County	237	23,890	76	25,352
Nevada–Balance	197	13,277	118	13,456
New Hampshire	269	12,854	151	13,626
New Jersey	1,362	96,698	789	100,973
New Mexico–Albuquerque	102	6,704	46	6,493
New Mexico–Balance	336	17,887	190	18,904
New York–New York City	820	67,351	512	66,309
New York–Balance	1,700	127,280	1,035	131,020
North Carolina–Charlotte	111	11,430	45	11,436
North Carolina–Guilford County	73	5,440	29	5,497
North Carolina–Balance	1,322	101,198	710	105,409
North Dakota	264	9,116	180	8,823
Ohio–Cleveland	80	3,265	78	3,179
Ohio–Balance	1,587	122,148	983	127,080
Oklahoma	840	51,807	588	52,202
Oregon	754	43,807	419	45,433
Pennsylvania–Philadelphia	147	10,490	120	9,339
Pennsylvania–Balance	1,396	117,460	769	124,275
Rhode Island	166	10,460	63	10,922

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Assessment.

South Carolina	656	58,707	318	59,887
South Dakota	314	10,725	252	11,013
Tennessee–Shelby County	119	8,885	62	7,965
Tennessee–Balance	906	67,289	551	68,972
Texas–Austin	81	6,112	21	5,558
Texas–Dallas	148	11,497	41	10,336
Texas–Fort Worth	85	6,196	33	6,049
Texas–Houston	176	16,509	60	13,143
Texas–Balance	4,124	359,068	2,204	380,080
Utah	650	51,190	275	53,345
Vermont	208	5,916	116	5,867
Virginia	1,110	96,163	383	99,765
Washington	1,256	84,888	631	86,202
West Virginia	387	19,055	180	19,653
Wisconsin–Milwaukee	112	5,563	79	4,964
Wisconsin–Balance	969	53,828	568	56,942
Wyoming	187	7,286	91	7,664
Other jurisdictions
Bureau of Indian Education (BIE)	136	3,066	110	2,742
Department of Defense Education Activity (DoDEA)	89	5,708	60	4,671
District of Columbia (TUDA)	79	4,034	32	3,013
District of Columbia–Balance	50	2,573	44	2,624
Puerto Rico	531	20,203	345	22,853

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/fourth_and_eighth_grade_schools_and_enrollment_in_the_2022_state_assess_sampling_frame.aspx

NAEP Technical Documentation New-School Sampling Frame for the 2022 State Assessment

The primary sampling frames for the 2022 fourth- and eighth-grade public school samples for the state assessment in mathematics and reading were constructed using the most current Common Core of Data (CCD) file available from NCES. This file contained schools that were in existence during the 2019-2020 school year (i.e., it was two years out of date). During the subsequent 2-year period, undoubtedly some schools closed, some changed structure (one school becoming two schools, for example), some newly opened, and still others changed their grade span.

2020 CCD file. The Coordinators were asked to add in any new schools and update grade span for the schools on this list.

districts in jurisdictions where all schools were selected for sample at either grade 4 or 8; state-operated districts;

districts in states with fewer than 10 districts;

charter-only districts (that is, districts containing no schools other than charter schools); and TUDA districts.

Then noncertainty districts were classified as small, medium, or large based on the number of schools and student enrollment of schools from the CCD-based public school frame.

A district was considered to be small if it contained no more than one school at each targeted grade (4 and 8). During school recruitment, the Coordinators were asked to identify schools within their district that newly offered the targeted grade. Every identified new school was added to the sample. From a sampling perspective, the new school was viewed as an “annex” to the sampled school which meant that it had a well-defined probability of selection equal to that of the sampled school. When a school in a small district was sampled from the CCD-based frame, its associated new school was automatically sampled as well.

A simplified example is given below. The state's districts are ordered by descending percentage enrollment. The first six become large districts and the last six become medium districts.

Large-size and medium-size district strata example, by enrollment, stratum, and district, 2022

District	Percentage enrollment	Cumulative percentage enrollment	Stratum
1	20	20	L
2	20	40	L
3	15	55	L

District Percentage enrollment Cumulative percentage enrollment Stratum

4	10	65	L
5	10	75	L
6	10	85	L
7	5	90	M
8	2	92	M
9	2	94	M
10	2	96	M
11	2	98	M
12	2	100	M
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics and Reading Assessments.

The following table presents the number and percentage of schools and average estimated grade enrollment for the fourth- and eighth-grade new-school frame by census region.

Number and percentage of schools and mean school size in the new-school frame, state assessment, by grade and census region: 2022

Census region	Grade 4			Grade 8
Census region	Schools	Percentage	Mean school size	Schools	Percentage	Mean school size
Total	259	100.00	57	343	100.00	57
Northeast	21	8.11	66	51	14.87	104
¹Outlying areas are not classified by census region. They include schools in Puerto Rico and Department of Defense Education

Activity (DoDEA) schools not located in the 50 states or the District of Columbia. NOTE: Detail may not sum to totals because of rounding.

Census region

Grade 4 Grade 8

Shape176

Schools Percentage Mean school size Schools Percentage Mean school size

Midwest	53	20.46	36	68	19.83	36
South	129	49.81	61	159	46.36	51
West	50	19.31	58	62	18.08	54
Outlying areas¹	6	2.32	94	3	0.87	109

¹Outlying areas are not classified by census region. They include schools in Puerto Rico and Department of Defense Education Activity (DoDEA) schools not located in the 50 states or the District of Columbia.

NOTE: Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/new_school_sampling_frame_for_the_2022_state_assessment.aspx

Shape177

NAEP Technical Documentation School and Student Participation in the 2022 State Assessment

The tables linked to the right present weighted school and student participation rates and weighted student exclusion and full-time remote rates for the fourth- and eighth-grade public school state assessment samples.

A weighted school participation rate indicates the percentage of the student population that is directly represented by the participating school sample.

A weighted student participation rate indicates the percentage of the student population that is directly represented by the assessed students from within participating schools.

A weighted full-time remote rate indicates the percentage of the student population that is full-time remote.

Weighted school participation rates are calculated by dividing the sum of school base weights, weighted by student enrollment of the targeted grade, for all participating schools by the sum of the base weights, weighted by student enrollment of the target grade, for all eligible schools. Eligible schools are all sampled schools except those considered out-of-scope. The base weight is assigned to all sampled schools and is the inverse of the probability of selection. The weighted school participation rates in these tables reflect participation prior to

Weighted Response Rates of Fourth-Grade School Sample by Participating Jurisdiction

Weighted Response Rates of Eighth-Grade School Sample by Participating Jurisdiction

Weighted Student Response and Exclusion Rates for Mathematics

Weighted Student Response and Exclusion Rates for Reading

Weighted Student Remote Rates by Participating Jurisdiction

substitution. That is, participating substitute schools that took the place of refusing originally sampled schools are not included in the numerator.

Every student sampled for NAEP is classified into one of the following response disposition categories: Assessed

Absent

Excluded (must be SD, EL, or SD and EL) Withdrawn or Graduated (ineligible)

Full-time remote

Assessed students were students that completed an assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_and_student_participation_in_the_2022_state_assessment.aspx

NAEP Technical Documentation Weighted Response Rates of Eighth-Grade School Sample by Participating Jurisdiction for the 2022 State Assessment

The following table presents unweighted counts of eligible sampled and participating schools and weighted school response rates, by participating jurisdiction, for the eighth- grade public school state assessment sample. States with Trial Urban District Assessment (TUDA) districts are shown in multiple rows: for the TUDA district(s) and for the state as a whole (the TUDA district[s] plus the rest of the state).

Eligible and participating school counts and weighted school response rates for eighth-grade mathematics and reading state assessments, by jurisdiction: 2022

Jurisdiction	Number of sampled eligible schools	Number of participating schools	Weighted school response rates (percent)
Total	5,250	5,220	99.60
Alabama	90	90	100.00
Alaska	100	100	98.71
Arizona	90	90	100.00
Arkansas	90	90	100.00
California–Los Angeles	60	60	100.00
California–San Diego	30	30	100.00
California	170	170	100.00
Colorado–Denver	40	40	92.34
Colorado	120	110	96.76
Connecticut	80	80	98.77
Delaware	50	50	100.00
Florida–Duval County	40	40	100.00
Florida–Hillsborough County	40	40	100.00
Florida–Miami-Dade County	60	60	100.00
Florida	200	200	100.00
Georgia–Atlanta	30	30	100.00
Georgia	110	110	100.00
Hawaii	50	50	100.00
Idaho	80	80	100.00
Illinois–Chicago	70	70	100.00
Illinois	140	140	100.00
Indiana	80	80	98.83
Iowa	80	80	100.00
Kansas	90	90	100.00
Kentucky–Jefferson County	20	20	100.00
Kentucky	100	100	100.00
NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

Louisiana	90	90	100.00
Maine	90	90	97.56
Maryland–Baltimore	40	40	100.00
Maryland	120	120	100.00
Massachusetts–Boston	40	40	100.00
Massachusetts	120	120	100.00
Michigan–Detroit	40	40	100.00
Michigan	130	130	100.00
Minnesota	80	80	98.62
Mississippi	80	80	100.00
Missouri	90	90	100.00
Montana	100	100	99.95
Nebraska	100	100	100.00
Nevada–Clark County	50	50	100.00
Nevada	90	90	100.00
New Hampshire	80	80	98.97
New Jersey	90	80	98.85
New Mexico–Albuquerque	30	30	100.00
New Mexico	100	100	100.00
New York–New York City	70	60	96.75
New York	120	120	97.65
North Carolina–Charlotte	30	30	100.00
North Carolina–Guilford County	20	20	100.00
North Carolina	130	130	100.00
North Dakota	80	80	100.00
Ohio–Cleveland	50	50	100.00
Ohio	130	130	100.00
Oklahoma	90	90	100.00
Oregon	90	90	100.00
Pennsylvania–Philadelphia	40	40	91.14
Pennsylvania	120	120	99.42
Rhode Island	60	60	100.00
South Carolina	90	90	100.00
South Dakota	90	90	98.95

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

Tennessee–Shelby County	40	40	100.00
Tennessee	110	110	97.51
Texas–Austin	20	20	100.00
Texas–Dallas	40	40	100.00
Texas–Fort Worth	20	20	100.00
Texas–Houston	40	40	100.00
Texas	200	200	100.00
Utah	90	90	100.00
Vermont	90	90	100.00
Virginia	80	80	98.75
Washington	90	90	100.00
West Virginia	90	90	100.00
Wisconsin–Milwaukee	40	40	100.00
Wisconsin	130	130	100.00
Wyoming	60	60	100.00
Other jurisdictions
Department of Defense Education Activity (DoDEA)	50	40	94.14
District of Columbia (TUDA)	20	20	100.00
District of Columbia	70	70	100.00
Puerto Rico	150	150	100.00

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_response_rates_of_eighth_grade_school_sample_by_participating_jurisdiction_for_the_2022_state_assess.aspx

Shape183

NAEP Technical Documentation Weighted Response Rates of Fourth-Grade School Sample by Participating Jurisdiction for the 2022 State Assessment

The following table presents unweighted counts of eligible sampled and participating schools and weighted school response rates, by participating jurisdiction, for the fourth- grade public school state assessment sample. States with Trial Urban District Assessment (TUDA) districts are shown in multiple rows: for the TUDA district(s) and for the state as a whole (the TUDA district[s] plus the rest of the state).

Eligible and participating school counts and weighted school response rates for fourth-grade mathematics and reading state assessments, by jurisdiction: 2022

Jurisdiction	Number of sampled eligible schools	Number of participating schools	Weighted school response rates (percent)
Total	5,830	5,800	99.51
Alabama	90	90	100.00
Alaska	130	120	99.20
Arizona	90	90	100.00
Arkansas	80	80	100.00
California–Los Angeles	60	60	100.00
California–San Diego	40	40	100.00
California	180	180	100.00
Colorado–Denver	40	40	100.00
Colorado	120	120	99.04
Connecticut	80	80	100.00
Delaware	70	70	100.00
Florida–Duval County	40	40	100.00
Florida–Hillsborough County	40	40	100.00
Florida–Miami-Dade County	60	60	100.00
Florida	210	210	100.00
Georgia–Atlanta	40	40	100.00
Georgia	120	120	96.17
Hawaii	90	90	100.00
Idaho	90	90	100.00
Illinois–Chicago	70	70	100.00
Illinois	140	140	100.00
Indiana	90	80	98.63
Iowa	90	90	98.67
Kansas	100	100	100.00
Kentucky–Jefferson County	40	40	100.00
Kentucky	110	110	100.00
Louisiana	80	80	100.00
Maine	110	110	100.00
Maryland–Baltimore	40	40	100.00
NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

Maryland	120	120	100.00
Massachusetts–Boston	50	50	100.00
Massachusetts	130	130	100.00
Michigan–Detroit	40	40	100.00
Michigan	130	130	100.00
Minnesota	90	90	100.00
Mississippi	90	90	100.00
Missouri	90	90	100.00
Montana	120	120	99.95
Nebraska	100	100	100.00
Nevada–Clark County	60	60	100.00
Nevada	90	90	100.00
New Hampshire	100	100	99.15
New Jersey	90	80	98.72
New Mexico–Albuquerque	40	40	100.00
New Mexico	110	110	100.00
New York–New York City	70	60	98.73
New York	120	120	95.76
North Carolina–Charlotte	40	40	100.00
North Carolina–Guilford County	40	40	100.00
North Carolina	160	160	100.00
North Dakota	120	110	99.28
Ohio–Cleveland	50	50	100.00
Ohio	130	130	100.00
Oklahoma	90	90	100.00
Oregon	90	90	100.00
Pennsylvania–Philadelphia	40	40	98.11
Pennsylvania	120	120	99.86
Rhode Island	90	90	100.00
South Carolina	90	90	100.00
South Dakota	120	120	100.00
Tennessee–Shelby County	40	40	100.00
Tennessee	120	120	100.00
Texas–Austin	40	40	100.00

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

Texas–Dallas	40	40	100.00
Texas–Fort Worth	40	40	100.00
Texas–Houston	60	60	100.00
Texas	260	260	100.00
Utah	80	80	100.00
Vermont	130	130	100.00
Virginia	80	80	100.00
Washington	90	90	100.00
West Virginia	100	100	100.00
Wisconsin–Milwaukee	50	50	100.00
Wisconsin	130	130	100.00
Wyoming	100	90	98.78
Other jurisdictions
Department of Defense Education Activity (DoDEA)	90	80	94.55
District of Columbia (TUDA)	50	50	100.00
District of Columbia	90	90	100.00
Puerto Rico	150	150	100.00

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_response_rates_of_fourth_grade_school_sample_by_participating_jurisdiction_for_the_2022_state_assess.aspx

Shape192

NAEP Technical Documentation Weighted Student Remote Rates by Participating Jurisdiction for the 2022 State Assessment

In 2022 as a result of the COVID-19 pandemic, there was interest in determining the extent to which students were receiving their education through full-time remote learning. Full-time remote students are enrolled in brick-and-mortar schools but do not attend school in person. They are considered not assessable for NAEP.

The following table presents weighted student full-time remote rates by grade, subject, and participating jurisdiction, for the public school state assessment samples. States with Trial Urban District Assessment (TUDA) districts are shown in multiple rows: for the TUDA district(s) and for the state as a whole (the TUDA district[s] plus the rest of the state).

The weighted student full-time remote rate indicates the percentage of the student population that is full-time remote.

Weighted student full-time remote rates, state assessment, by grade, subject, and jurisdiction: 2022

Jurisdiction	Grade 4 mathematics (percent)	Grade 4 reading (percent)	Grade 8 mathematics (percent)	Grade 8 reading (percent)
National public	0.78	0.73	1.29	1.32
Alabama	0.39	0.41	0.79	0.70
Alaska	0.96	1.41	1.94	1.75
Arizona	0.42	0.37	1.25	0.80
Arkansas	1.27	1.52	2.33	2.26
California–Los Angeles	0.11	0.36	0.83	0.62
California–San Diego	0.32	0.10	0.00	0.00
California	0.71	0.30	1.12	0.86
Colorado–Denver	0.00	0.00	0.44	0.52
Colorado	0.34	0.32	0.22	0.46
Connecticut	0.00	0.06	0.05	0.06
Delaware	2.05	1.68	1.64	1.56
Florida–Duval County	0.00	0.00	0.08	0.00
Florida–Hillsborough County	0.00	0.00	0.00	0.00
Florida–Miami-Dade County	0.00	0.00	0.00	0.00
Florida	0.00	0.06	1.02	0.97
Georgia–Atlanta	2.09	2.05	4.46	3.49
Georgia	2.00	1.97	2.39	2.97
Hawaii	4.80	4.39	6.22	6.01
Idaho	0.32	0.24	0.97	0.74
Illinois–Chicago	0.00	0.00	0.00	0.13
Illinois	0.00	0.18	0.67	0.60
Indiana	0.79	0.94	1.99	2.69
Iowa	0.47	0.24	0.93	0.95
Kansas	0.14	0.10	0.53	0.33
Kentucky–Jefferson County	0.29	0.10	0.00	0.08
Kentucky	1.11	0.65	2.08	2.66
Louisiana	0.77	0.90	2.42	2.06
Maine	0.37	0.20	0.75	0.53
Maryland–Baltimore	1.19	1.11	0.70	0.82
Maryland	3.04	2.60	1.36	1.05
† Not applicable.

Jurisdiction

Grade 4 mathematics

(percent)

Grade 4 reading

(percent)

Grade 8 mathematics

(percent)

Grade 8 reading

(percent)

Massachusetts–Boston	0.46	0.13	0.00	0.00
Massachusetts	0.02	0.01	0.09	0.00
Michigan–Detroit	0.80	0.63	0.59	0.40
Michigan	1.76	1.89	2.19	2.96
Minnesota	0.91	0.78	0.15	0.15
Mississippi	0.37	0.51	0.46	0.44
Missouri	1.95	0.86	2.91	3.69
Montana	0.72	0.43	1.42	1.43
Nebraska	0.08	0.10	0.20	0.23
Nevada–Clark County	0.06	0.00	0.91	1.09
Nevada	0.19	0.21	0.60	0.95
New Hampshire	0.04	0.08	0.09	0.05
New Jersey	0.25	0.04	0.15	0.21
New Mexico–Albuquerque	0.45	0.38	0.00	0.00
New Mexico	1.71	1.60	2.24	2.65
New York–New York City	0.07	0.07	0.13	0.00
New York	0.09	0.02	0.20	0.13
North Carolina–Charlotte	0.00	0.11	0.00	0.00
North Carolina–Guilford County	0.00	0.00	0.00	0.00
North Carolina	0.58	1.05	1.92	1.45
North Dakota	0.04	0.05	0.29	0.42
Ohio–Cleveland	0.12	0.23	0.34	0.22
Ohio	0.22	0.06	0.87	0.96
Oklahoma	1.05	1.20	2.92	2.81
Oregon	1.51	1.89	3.22	3.67
Pennsylvania–Philadelphia	0.11	0.00	0.00	0.00
Pennsylvania	2.12	2.16	3.71	4.68
Rhode Island	0.05	0.00	0.12	0.17
South Carolina	1.92	3.14	3.48	2.41
South Dakota	0.30	0.05	0.64	0.59
Tennessee–Shelby County	0.00	0.00	0.00	0.00
Tennessee	0.00	0.05	0.04	0.26
Texas–Austin	0.11	0.00	0.00	0.00

† Not applicable.

Jurisdiction

Grade 4 mathematics

(percent)

Grade 4 reading

(percent)

Grade 8 mathematics

(percent)

Grade 8 reading

(percent)

Texas–Dallas	0.40	0.60	0.18	0.00
Texas–Fort Worth	0.09	0.00	0.00	0.00
Texas–Houston	0.32	0.16	0.00	0.00
Texas	0.57	0.56	0.20	0.29
Utah	1.41	1.38	1.42	1.35
Vermont	0.15	0.10	0.16	0.38
Virginia	1.54	1.46	4.03	3.93
Washington	0.23	0.31	1.08	0.85
West Virginia	2.26	1.45	2.77	2.56
Wisconsin–Milwaukee	0.58	0.12	0.70	0.99
Wisconsin	0.43	0.46	1.05	0.73
Wyoming	2.82	2.43	4.50	3.73
Other jurisdictions
Department of Defense Education Activity (DoDEA)	0.79	1.10	1.06	1.35
District of Columbia (TUDA)	0.48	0.44	0.89	0.44
District of Columbia	0.99	0.79	1.07	0.95
Puerto Rico	1.09	†	1.44	†

† Not applicable.

NOTE: Detail may not sum to totals because of rounding.

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_remote_rates_by_participating_jurisdiction_for_the_2022_state_assessment.aspx

Shape201

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 State Mathematics Assessment

The following table presents weighted student response and exclusion rates, by participating jurisdiction, for the fourth- and eighth-grade public school state assessment samples. States with Trial Urban District Assessment (TUDA) districts are shown in multiple rows: for the TUDA district(s) and for the state as a whole (the TUDA district[s] plus the rest of the state).

Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response and exclusion rates for public schools, state mathematics assessment, by grade and jurisdiction: 2022

		Grade 4			Grade 8
Jurisdiction	Weighted student response rates (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded	Weighted student response rates (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded
Total	91.78	1.47	0.71	88.69	1.20	0.60
Alabama	94.68	1.08	0.24	91.21	1.34	0.30
Alaska	88.61	0.83	0.41	83.79	0.99	0.46
Arizona	92.83	0.91	0.55	90.30	1.44	0.31
Arkansas	92.58	0.68	0.37	91.18	0.81	0.26
California–Los Angeles	91.97	1.40	1.21	88.71	1.53	1.00
California–San Diego	88.61	1.35	1.92	85.52	1.05	1.18
California	91.91	1.66	1.18	88.05	1.27	1.16
Colorado–Denver	88.86	0.64	1.80	87.68	2.14	1.15
Colorado	91.10	1.28	0.64	86.46	1.10	0.33
Connecticut	91.79	1.49	1.02	87.84	1.27	0.62
Delaware	91.03	1.18	0.77	87.27	1.44	0.51
Florida–Duval County	91.75	2.07	0.00	91.37	1.53	0.00
Florida–Hillsborough County	92.13	2.16	0.98	90.53	1.03	1.22
Florida–Miami-Dade County	94.64	1.27	2.00	91.25	1.96	1.62
Florida	91.80	1.89	0.94	89.47	1.96	0.59
Georgia–Atlanta	93.69	0.78	0.22	90.39	0.69	0.21
Georgia	92.84	1.12	0.37	90.25	1.48	0.41
Hawaii	88.53	1.24	0.74	85.29	1.47	0.81
Idaho	93.22	0.80	0.12	90.48	1.18	0.15
Illinois–Chicago	90.39	1.96	1.42	88.15	0.70	0.48
Illinois	91.19	1.06	0.51	87.95	0.84	0.47
Indiana	92.77	0.45	0.17	90.54	0.46	0.31
Iowa	93.08	1.21	0.40	90.13	1.15	0.38
Kansas	92.88	1.06	0.41	91.03	0.95	0.47
Kentucky–Jefferson County	93.68	2.46	1.33	91.05	1.29	0.26
Kentucky	94.50	1.56	0.44	89.43	1.95	0.38
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics Assessment.

Shape202

	Grade 4			Grade 8
Weighted	Weighted	Weighted	Weighted	Weighted	Weighted
student	percentage of	percentage of	student	percentage of	percentage of
response	all students who	all students who	response	all students who	all students who
rates	were SD and	were EL and	rates	were SD and	were EL and
(percent)	excluded	excluded	(percent)	excluded	excluded

Jurisdiction

Louisiana	92.36	1.55	0.06	89.70	1.91	0.36
Maine	90.46	1.37	0.29	86.84	0.77	0.27
Maryland–Baltimore	89.82	0.84	0.55	90.04	2.06	0.90
Maryland	92.09	0.73	0.74	89.06	1.14	0.93
Massachusetts–Boston	90.83	3.52	3.86	88.86	4.22	3.96
Massachusetts	92.84	1.31	0.77	87.89	1.04	1.81
Michigan–Detroit	89.97	3.96	0.15	88.79	4.47	0.74
Michigan	91.18	2.59	0.48	86.82	1.58	0.29
Minnesota	90.79	2.11	0.77	85.74	1.55	0.65
Mississippi	92.78	0.71	0.10	90.09	0.72	0.22
Missouri	94.35	0.78	0.14	91.73	0.65	0.33
Montana	89.77	0.95	0.05	85.81	1.17	0.10
Nebraska	94.76	1.19	0.04	92.46	1.40	0.36
Nevada–Clark County	92.17	0.97	0.69	85.93	0.99	0.85
Nevada	92.26	1.58	0.56	87.92	0.92	0.65
New Hampshire	86.89	1.03	0.25	82.00	1.29	0.19
New Jersey	92.15	1.23	0.93	91.20	0.77	0.83
New Mexico–Albuquerque	91.29	0.46	0.17	85.50	1.37	1.01
New Mexico	90.58	1.40	0.48	88.36	1.43	0.52
New York–New York City	87.37	0.25	1.01	83.59	0.45	0.49
New York	86.46	0.69	0.59	81.09	1.22	0.51
North Carolina–Charlotte	92.44	1.13	1.68	89.89	1.63	1.81
North Carolina–Guilford County	92.62	1.35	0.11	89.25	1.58	0.44
North Carolina	90.96	1.19	1.08	90.32	0.79	0.46
North Dakota	90.24	1.11	0.23	88.51	1.25	0.17
Ohio–Cleveland	88.77	2.44	0.41	87.12	2.85	1.20
Ohio	92.78	0.94	0.33	89.59	0.78	0.39
Oklahoma	93.65	2.17	0.36	92.11	1.30	0.44
Oregon	87.89	1.11	0.67	84.92	0.98	0.76
Pennsylvania–Philadelphia	93.65	3.18	1.47	86.81	2.86	2.16
Pennsylvania	92.53	1.54	0.51	89.04	1.04	0.35

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics Assessment.

Shape203

	Grade 4			Grade 8
Weighted	Weighted	Weighted	Weighted	Weighted	Weighted
student	percentage of	percentage of	student	percentage of	percentage of
response	all students who	all students who	response	all students who	all students who
rates	were SD and	were EL and	rates	were SD and	were EL and
(percent)	excluded	excluded	(percent)	excluded	excluded

Jurisdiction

Rhode Island	94.25	1.01	0.73	90.48	1.39	1.09
South Carolina	93.01	0.75	0.36	91.36	1.03	0.54
South Dakota	93.78	1.04	0.24	91.16	1.41	0.21
Tennessee–Shelby County	94.05	2.33	1.41	90.34	2.53	0.23
Tennessee	92.04	1.89	0.64	90.98	1.77	0.64
Texas–Austin	87.96	2.18	1.94	84.80	1.45	1.31
Texas–Dallas	91.71	3.08	2.06	91.02	1.68	1.20
Texas–Fort Worth	93.11	1.89	0.59	91.81	2.03	0.74
Texas–Houston	93.43	2.52	1.15	88.66	1.45	1.72
Texas	92.75	2.35	1.18	89.72	1.11	0.67
Utah	92.24	0.90	0.29	87.70	1.27	0.54
Vermont	88.80	1.32	0.09	87.05	1.50	0.22
Virginia	91.98	2.25	1.05	88.42	1.18	0.87
Washington	89.21	1.74	0.88	86.92	1.17	0.34
West Virginia	92.64	1.59	0.05	90.99	1.32	0.26
Wisconsin–Milwaukee	86.42	1.00	0.56	80.38	1.91	0.67
Wisconsin	90.27	1.15	0.45	87.83	1.06	0.24
Wyoming	90.11	1.17	0.10	87.33	1.24	0.25
Other jurisdictions
Department of Defense Education Activity (DoDEA)	88.71	1.43	0.29	89.55	0.89	0.23
District of Columbia (TUDA)	89.57	1.93	1.64	81.92	2.27	1.77
District of Columbia	88.24	1.37	1.05	82.67	1.80	1.04
Puerto Rico	92.19	0.10	0.06	91.07	0.02	0.04

SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics Assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_state_mathematics_assessment.aspx

Shape204

NAEP Technical Documentation Weighted Student Response and Exclusion Rates for the 2022 State Reading Assessment

Separate exclusion rates are provided for students with disabilities (SD) and English learners (EL).

Weighted student response and exclusion rates for public schools, state reading assessment, by grade and jurisdiction: 2022

		Grade 4			Grade 8
Jurisdiction	Weighted student response rates (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded	Weighted student response rates (percent)	Weighted percentage of all students who were SD and excluded	Weighted percentage of all students who were EL and excluded
Total	91.60	1.55	0.78	88.82	1.41	0.71
Alabama	93.53	0.76	0.47	92.41	0.74	0.24
Alaska	88.73	0.57	0.09	82.03	0.38	0.17
Arizona	92.25	0.90	0.41	89.78	1.56	0.26
Arkansas	93.87	1.35	0.38	91.43	1.19	0.55
California–Los Angeles	92.38	1.20	1.59	89.78	1.47	1.33
California–San Diego	88.59	1.77	1.88	88.48	1.83	0.51
California	91.45	1.93	1.09	88.09	1.70	1.59
Colorado–Denver	90.68	1.52	2.43	88.48	1.77	1.52
Colorado	91.37	1.94	1.17	86.94	1.29	0.96
Connecticut	88.93	1.23	1.45	88.43	1.32	0.63
Delaware	89.69	1.05	0.39	87.58	1.05	0.52
Florida–Duval County	93.11	2.08	0.00	92.24	1.77	0.08
Florida–Hillsborough County	93.93	1.52	1.50	88.96	1.66	1.62
Florida–Miami-Dade County	92.83	1.26	1.88	90.11	1.67	1.79
Florida	93.05	1.08	1.32	87.36	1.76	0.66
Georgia–Atlanta	92.78	2.56	0.62	90.57	2.62	0.32
Georgia	92.18	1.26	0.70	92.79	1.66	0.37
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Reading Assessment.

Shape205

	Grade 4			Grade 8
Weighted	Weighted	Weighted	Weighted	Weighted	Weighted
student	percentage of	percentage of	student	percentage of	percentage of
response	all students who	all students who	response	all students who	all students who
rates	were SD and	were EL and	rates	were SD and	were EL and
(percent)	excluded	excluded	(percent)	excluded	excluded

Jurisdiction

Hawaii	88.58	1.07	0.27	83.42	1.26	0.40
Idaho	92.45	1.58	0.26	91.03	1.41	0.62
Illinois–Chicago	89.02	1.90	1.18	88.67	1.26	0.87
Illinois	90.91	0.73	0.50	88.38	0.97	0.50
Indiana	93.09	0.35	0.32	90.34	0.28	0.28
Iowa	92.99	0.91	0.31	90.16	0.78	0.44
Kansas	93.24	0.92	0.10	92.93	1.11	0.26
Kentucky–Jefferson County	92.34	3.53	3.25	91.78	1.78	0.36
Kentucky	93.45	2.47	0.81	91.10	1.76	0.50
Louisiana	92.12	2.01	0.43	89.24	2.33	0.53
Maine	92.02	0.81	0.33	89.52	1.07	0.31
Maryland–Baltimore	90.67	1.61	1.61	90.61	2.05	0.88
Maryland	91.81	1.07	1.00	90.36	0.98	1.08
Massachusetts–Boston	90.96	4.17	3.54	87.12	2.92	4.15
Massachusetts	92.98	1.80	1.04	88.83	1.15	1.79
Michigan–Detroit	89.44	4.02	0.41	87.61	4.78	0.70
Michigan	90.98	2.24	0.54	86.24	1.30	0.25
Minnesota	91.18	3.11	1.02	84.69	1.26	0.82
Mississippi	92.70	1.31	0.00	91.75	0.58	0.10
Missouri	93.38	0.66	0.18	92.49	0.90	0.30
Montana	89.73	1.32	0.00	87.24	0.79	0.05
Nebraska	94.33	1.02	0.27	92.69	1.13	0.34
Nevada–Clark County	91.94	1.08	0.91	86.43	1.12	0.48
Nevada	91.47	1.08	0.67	88.06	1.06	0.39
New Hampshire	87.70	1.06	0.13	84.57	0.71	0.33
New Jersey	91.90	2.13	0.77	89.50	1.60	0.71
New Mexico–Albuquerque	91.29	1.05	0.67	86.92	1.02	0.20
New Mexico	91.03	1.19	0.35	87.17	1.56	0.32
New York–New York City	87.42	0.92	1.59	84.41	0.51	0.60
New York	86.57	1.52	0.86	81.82	1.60	0.72
North Carolina–Charlotte	91.77	0.93	0.87	89.31	1.02	2.05

Shape211

	Grade 4			Grade 8
Weighted	Weighted	Weighted	Weighted	Weighted	Weighted
student	percentage of	percentage of	student	percentage of	percentage of
response	all students who	all students who	response	all students who	all students who
rates	were SD and	were EL and	rates	were SD and	were EL and
(percent)	excluded	excluded	(percent)	excluded	excluded

Jurisdiction

North Carolina–Guilford County	91.77	1.61	0.21	89.39	0.92	0.18
North Carolina	91.11	1.33	0.58	89.15	1.47	0.54
North Dakota	91.16	1.52	0.23	88.82	1.37	0.22
Ohio–Cleveland	87.53	1.84	0.40	89.60	2.72	1.44
Ohio	92.35	2.03	0.43	89.39	1.02	0.47
Oklahoma	92.40	1.50	0.35	92.72	2.02	0.72
Oregon	89.66	1.70	0.47	85.28	0.80	0.38
Pennsylvania–Philadelphia	93.38	4.10	3.05	88.26	3.26	2.24
Pennsylvania	91.83	1.67	0.59	89.13	1.34	0.51
Rhode Island	93.82	0.69	0.50	89.57	1.31	0.60
South Carolina	92.09	1.24	0.43	92.35	0.75	0.61
South Dakota	93.95	0.88	0.16	91.64	1.30	0.49
Tennessee–Shelby County	91.22	3.25	0.57	89.30	2.29	0.45
Tennessee	91.68	1.63	0.61	89.14	2.29	0.57
Texas–Austin	89.14	2.76	3.88	86.68	1.55	1.10
Texas–Dallas	92.41	2.05	3.03	93.27	1.84	1.98
Texas–Fort Worth	91.01	2.77	1.38	91.91	1.32	0.30
Texas–Houston	92.05	1.86	0.71	89.49	1.78	2.26
Texas	92.44	2.10	1.34	90.81	1.74	0.70
Utah	92.30	0.54	0.59	87.55	0.71	0.65
Vermont	89.00	1.18	0.32	86.98	1.51	0.20
Virginia	91.86	1.81	0.78	89.02	1.66	1.57
Washington	88.85	1.53	0.62	85.49	1.35	0.43
West Virginia	90.27	1.63	0.03	90.88	1.58	0.15
Wisconsin–Milwaukee	85.33	1.41	0.91	83.36	0.69	0.52
Wisconsin	90.73	0.76	0.29	88.02	0.57	0.30
Wyoming	91.74	1.56	0.43	87.19	1.20	0.48
Other jurisdictions
Department of Defense Education Activity (DoDEA)	89.71	1.18	0.74	89.68	1.15	0.63
District of Columbia (TUDA)	88.64	3.89	2.41	83.17	2.74	2.31
District of Columbia	87.75	3.07	1.53	83.75	2.12	1.38

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/weighted_student_response_and_exclusion_rates_for_the_2022_state_reading_assessment.aspx

Shape212

NAEP Technical Documentation School Sample Selection for the 2022 State Assessment

The sampled schools for the fourth- and eighth-grade public school state assessments in mathematics and reading came from two frames: the primary public school sample frame constructed from the Common Core of Data (CCD) and the supplemental new-school sampling frame. Schools were sampled from each school frame with probability proportional to size (PPS) using systematic sampling. Prior to sampling, schools in each frame were sorted by the appropriate implicit stratification variables in a serpentine order. A school's measure of size was a complex function of the school's estimated grade enrollment. Schools whose measure of size was larger than the sampling interval could be selected or “hit” multiple times. Schools with multiple hits were selected with certainty and had larger student sample sizes.

For the CCD-based frame, schools were sampled at a rate that would yield specific target student sample sizes for each jurisdiction. All

Computation of Measures of Size

School Sample Sizes: Frame and New School

Evaluation of the Samples Using State Achievement Data

jurisdictions, except Puerto Rico, had a target student sample size of 4,100 students for grade 4, and 4,200 for grade 8. The goal was to obtain 3,500 assessed students per grade: 1,750 students for the reading operational assessments, and 1,750 students for the mathematics operational assessments. Puerto Rico had a target student sample size of 3,600 students per grade. By design, Bureau of Indian Education (BIE) schools were not part of the state assessments this year. However, separate BIE school samples were selected based on target student sample sizes that were large enough to ensure that BIE schools were sufficiently represented in the national samples.

The schools in the new-school frame were sampled at the same rate as the CCD-based school frame.

Prior to selection, schools were deeply stratified in each jurisdiction to ensure that the school sample distribution reflected the school population distribution as closely as possible, with regard to the stratification variables, to minimize sampling error. The success of this approach was shown by comparing the proportion of minorities enrolled in schools (based on CCD values for each school), median income, and urban-centric locale (viewed as an interval variable) reported in the original frame against the school sample.

In addition, the distribution of state assessment achievement scores for the original frame can be compared with that of the school sample for those jurisdictions for which state assessment achievement data are available, as was done in the evaluation of the samples using state achievement data.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_sample_selection_for_the_2022_state_assessment.aspx

Shape217

NAEP Technical Documentation Computation of Measures of Size for the 2022 State Assessment

In designing each school sample, six objectives underlie the process of determining the probability of selection for each school and how many students are to be sampled from each selected school containing the respective grade:

to meet the target student sample size for each grade; to select an equal-probability sample of students;

to limit the number of students selected from any one school;

to ensure that the sample within a school does not include a very high percentage of the students in the school, unless all students are included;

to reduce the sampling rate of small schools, in recognition of the greater cost and burden per student of conducting assessments in such schools; and

to ensure the inclusion of all eligible schools that were part of the NAEP 2021 Monthly School Survey and NAEP 2021 School and Teacher Questionnaire Study.

The goal in determining the school's measure of size (MOS) is to optimize across the middle four objectives in terms of maintaining the precision of estimates and the cost effectiveness of the sample design. In certain jurisdictions, a census of students was taken so as to meet, as nearly as possible, the target student sample size. Elsewhere, to meet the target student sample and achieve a reasonable compromise among the middle four objectives above, the following algorithm was used to assign a measure of size to each school based on its enrollment per grade as indicated on the sampling frame.

The preliminary measures of size were set as follows:

\begin{equation} MOS_{js} =

\left\{ \begin{array}{l}

x_{js} & \text{if } z_{js} < x_{js} \\[2pt]

y_{j} & \text{if } 20 < x_{js} \leq{z_{js}} \\[2pt]

\left(\dfrac{y_j}{20}\right) \times x_{js} & \text{if } 10 < x_{js} \leq {20} \\

\dfrac{y_j}{2} & x_{js} \leq {10} \end{array}\right.

\end{equation}

where `x_{js}` is the estimated grade enrollment for school `s` in jurisdiction `j`, `y_{j}` the target within-school student sample size for jurisdiction `j`, and `z_{js}` the within-school take-all student cutoff for jurisdiction `j` to which school `s` belongs.

For the state samples at grades 4 and 8, the target sample sizes and take-all cutoffs were 50 and 52 for all jurisdictions and TUDAs with the exception of Puerto Rico, where they were 25 and 26, respectively.

The preliminary measure of size reflects the need to lower the expected number of very small schools in the sample, as the marginal cost for each assessed student in these schools is higher. These very small schools are sampled at half the rate of the larger schools, and their weights are doubled to account for the half sampling.

To address the last bullet above, an adjustment was made to the preliminary measures of size in an attempt to ensure the inclusion of all eligible schools that were part of

the NAEP 2021 Monthly School Survey and NAEP 2021 School and Teacher Questionnaire Study sample. The NAEP sampling procedures used an adaptation of the Keyfitz process to compute conditional measures of size that, by design, maximized the overlap of schools selected for both years.

The preliminary school measure of size is rescaled to create an expected number of hits by applying a multiplicative constant $b_{j}$, which varies by jurisdiction $j$. One can choose a value of $b_{j}$ such that the expected overall student sample yield matches the desired target specified by the design, where the expected yield is calculated by

summing the product of an individual school's probability and its student yield across all schools in the frame. The final measure of size, `E_{js}`, is defined as:

\begin{equation}

E_{js}=min(b_{j}\times MOS_{js}, u_{j}),

\end{equation}

The quantity `u_{j}` (the maximum number of hits allowed) in this formula is designed to put an upper bound on the burden for the sampled schools. In most jurisdictions,

`u_{j}` was set to 3. At grades 4 and 8 in Alaska and grade 8 in DC, `u_{j}` was set to 8, and in Puerto Rico, `u_{j}` was set to 1.

In addition, new and newly-eligible schools were sampled from the new-school frame. The assigned measures of size for these schools,

\begin{equation}

E_{js}=min(b_{j}\times MOS_{js}\times \pi_{djs}^{-1} , u_{j}),

\end{equation}

used the `b_{j}` and `u_{j}` values from the CCD-based school frame for the jurisdiction (i.e., the same sampling rate as for the CCD-based school sample within each jurisdiction). The variable `pi_{djs}` is the probability of selection of the district into the new-school district (`d`) sample.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/computation_of_measures_of_size_for_the_2022_state_assessment.aspx

Shape218

NAEP Technical Documentation Evaluation of the Samples for the 2022 State Assessment Using State Achievement Data

The purpose of this analysis was to determine whether public schools selected for the 2022 samples were representative of the schools on the NAEP sampling frames in terms of student achievement. Percentiles of the achievement distributions were compared between the frame and school sample for each public school jurisdiction in grades 4 and 8.

Achievement Data

For grades 4 and 8, the achievement variable used in the analysis was the same variable used in the NAEP sample design to stratify the public school frame. For all jurisdictions in the analysis except Puerto Rico, the variable was an achievement score provided by the jurisdiction. However, for Puerto Rico, where achievement data were not available, the 2015–2019 American Community Survey (ACS) 5-year estimates for median household income were used. (Median household income was based on the five-digit zip code area in which the school was located.) The achievement data consisted of various types of school-specific achievement measures from state assessment programs. The type of achievement data available varied by jurisdiction. For instance, in some states, the measure was the average score for a given state assessment. In other states, the measure was a percentile rank or percentage of students above a specific score. For Connecticut at grade 4, for example, we used the percentage of students in grade 4 who scored at or above the proficient level on the state mathematics test.

During frame development, not every record on the Common Core of Data (CCD) file matched the achievement data files created for the National Center for Education Statistics (NCES), even in jurisdictions where those data were generally available. For schools that did not match, their achievement scores were imputed by a mean matching imputation approach using the mean achievement score for schools with complete achievement data within the same jurisdiction-urbanicity-race/ethnicity stratum combination.

Methodology

To determine whether the distributions of schools by achievement measure between the frame and school sample were different, comparisons of percentile estimates were made for the 10th, 25th, 50th, 75th, and 90th percentile levels as well as the mean for each public school jurisdiction by grade. Frame and school sample estimates were considered statistically different if the frame value fell outside the 95 percent confidence interval of the corresponding sample estimate. The percentile values for the frames were calculated by weighting each school by the estimated number of students in the given grade. The percentile estimates for the school samples were calculated using school weights and weighted by the school measure of size (estimated number of students in the given grade). The 95 percent confidence intervals for the school sample estimates were calculated in WesVar—software for computing estimates of sampling variance from complex sample survey (Westat, 2000b)—using the Woodruff method (Sarndal, Swensson, and Wretman 1992) with the use of a finite population correction factor.

Results

As mentioned above, sample and frame distributions of schools by achievement measure were determined to be different if at least one of the percentile estimates or the mean differed significantly at the 95 percent confidence level. Out of all the jurisdiction and grade comparisons (excluding jurisdictions where all schools in the frame were selected), only 64 of the 876 distributions compared were found to be significantly different. They are shown in the table below.

Summary of significant differences in achievement measures (median income) between the sample and the frame, state assessment, by grade and jurisdiction: 2022

Grade	Jurisdiction	Achievement data / median income	Estimate	Frame	Sample	Confidence interval
4	Illinois	Achievement data	10th percentile	9.80	6.74	(5.97, 9.52)
	Louisiana	Achievement data	10th percentile	40.33	37.98	(30.09, 40.31)
	New Jersey	Achievement data	10th percentile	23.56	22.01	(18.78, 22.85)
	New Mexico	Achievement data	50th percentile	25.97	27.63	(26.30, 28.60)
	New York	Achievement data	10th percentile	19.64	21.56	(20.19, 22.50)
	North Dakota	Achievement data	25th percentile	32.29	30.43	(27.13, 32.06)
	Puerto Rico	Median Income	75th percentile	23473.03	23214.50	(23079.13, 23349.87)
	Tennessee	Achievement data	10th percentile	21.25	24.05	(22.15, 26.31)
	Washington	Achievement data	50th percentile	55.14	57.97	(55.39, 58.66)
	Washington	Achievement data	90th percentile	79.44	75.83	(74.84, 78.31)
	Albuquerque	Achievement data	25th percentile	12.50	11.66	(10.63, 12.21)
	Austin	Achievement data	90th percentile	69.64	69.40	(69.36, 69.44)
	Baltimore	Achievement data	90th percentile	43.00	40.13	(36.97, 42.16)
	Charlotte-Mecklenburg	Achievement data	25th percentile	31.71	31.05	(30.91, 31.14)
	Chicago	Achievement data	25th percentile	10.71	12.54	(10.87, 13.81)
	Dallas	Achievement data	50th percentile	42.99	46.39	(46.37, 46.41)
	Dallas	Achievement data	75th percentile	53.85	55.64	(55.11, 56.17)
	Dallas	Achievement data	mean	45.25	46.12	(45.27, 46.96)
	Duval County (FL)	Achievement data	10th percentile	38.5	29.68	(24.23, 36.77)
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics and Reading Assessments.

Grade Jurisdiction

Achievement data /

median income Estimate Frame Sample Confidence interval

	Houston	Achievement data	50th percentile	38.75	37.22	(36.25, 38.71)
	Houston	Achievement data	mean	43.13	41.89	(41.29, 42.49)
	Jefferson County (KY)	Achievement data	10th percentile	9.66	9.85	(9.73, 9.93)
	New York City	Achievement data	50th percentile	48.96	47.00	(46.57, 48.46)
	Shelby County (TN)	Achievement data	50th percentile	32.02	31.17	(31.02, 31.31)
8	Arizona	Achievement data	10th percentile	13.84	12.58	(9.51, 13.07)
	Arizona	Achievement data	75th percentile	51.25	47.93	(45.35, 50.16)
	Arkansas	Achievement data	50th percentile	50.01	50.80	(50.09, 52.31)
	Hawaii	Achievement data	90th percentile	64.95	63.82	(63.34, 64.30)
	Idaho	Achievement data	90th percentile	62.55	57.26	(55.91, 61.82)
	Idaho	Achievement data	mean	41.25	39.78	(38.81, 40.74)
	Massachusetts	Achievement data	50th percentile	45.95	47.39	(46.74, 48.98)
	Michigan	Achievement data	50th percentile	42.82	39.47	(38.15, 42.71)
	Mississippi	Achievement data	25th percentile	28.60	25.27	(23.28, 28.58)
	Mississippi	Achievement data	50th percentile	47.07	46.45	(43.15, 47.04)
	Montana	Achievement data	90th percentile	53.50	52.39	(51.98, 52.82)
	Montana	Achievement data	mean	36.58	35.74	(34.95, 36.52)
	Nebraska	Achievement data	50th percentile	48.94	47.87	(47.18, 48.63)
	Nevada	Achievement data	10th percentile	12.22	12.42	(12.23, 13.35)
	New Mexico	Achievement data	90th percentile	37.07	31.48	(30.41, 36.68)
	Ohio	Achievement data	25th percentile	53.32	49.12	(44.01, 53.04)
	Oregon	Achievement data	25th percentile	28.55	26.78	(25.39, 27.74)
	Pennsylvania	Achievement data	90th percentile	54.15	52.63	(49.94, 53.62)
	Pennsylvania	Achievement data	mean	32.54	31.27	(30.27, 32.26)
	South Dakota	Achievement data	90th percentile	64.30	63.81	(63.29, 64.14)
	Utah	Achievement data	10th percentile	21.64	20.63	(18.77, 21.57)
	West Virginia	Achievement data	50th percentile	37.06	36.08	(34.18, 36.92)
	West Virginia	Achievement data	mean	36.77	36.05	(35.47, 36.64)
	Baltimore	Achievement data	50th percentile	7.21	6.23	(5.00, 6.56)
	Charlotte-Mecklenburg	Achievement data	75th percentile	58.86	60.10	(59.85, 60.35)
	Charlotte-Mecklenburg	Achievement data	90th percentile	75.56	75.48	(75.43, 75.53)
	Chicago	Achievement data	75th percentile	36.31	33.54	(32.32, 36.16)
	Duval County (FL)	Achievement data	75th percentile	71.28	68.33	(67.75, 69.04)
	Houston	Achievement data	50th percentile	57.90	55.74	(52.46, 57.8)
	Houston	Achievement data	75th percentile	67.56	65.81	(63.98, 67.05)

Grade Jurisdiction

Achievement data /

median income Estimate Frame Sample Confidence interval

Houston	Achievement data	mean	55.23	53.56	(52.06, 55.06)
Los Angeles	Achievement data	mean	2514.30	2520.07	(2515.28, 2524.85)
Milwaukee	Achievement data	75th percentile	24.73	23.61	(22.99, 24.22)
Milwaukee	Achievement data	mean	15.84	16.65	(15.88, 17.41)
New York City	Achievement data	25th percentile	22.99	18.88	(16.60, 22.5)
New York City	Achievement data	50th percentile	38.26	34.83	(33.82, 36.37)
New York City	Achievement data	mean	41.79	39.55	(38.01, 41.08)
Philadelphia City	Achievement data	50th percentile	10.40	9.03	(8.62, 10.36)
Philadelphia City	Achievement data	75th percentile	21.71	21.19	(21.08, 21.30)
Shelby County (TN)	Achievement data	90th percentile	48.93	49.67	(49.43, 50.35)

The number of significant differences found in this analysis was close to what would be expected, albeit slightly higher, given the large number of comparisons that were made. Also, the number of significant results were widely spread throughout different grades and jurisdictions. Even in the statistically significant cases, the close adherence of sample values to frame values suggests there is little evidence that the school sample for NAEP 2022 is not representative of the frame from which it was selected. The achievement/median-income variable is used as the third-level sort order variable in the school systematic selection procedure. While it may be a rather low level sort variable, it still helps control how representative the sampled schools are in terms of achievement. The close agreement between frame and sample values of these achievement/median- income variables provided assurance that the selected sample is representative of the frame with respect to achievement or income status.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/evaluation_of_the_samples_for_the_2022_state_assessment_using_state_achievement_data.aspx

NAEP Technical Documentation School Sample Sizes: CCD-Based and New- School Sampling Frames for the 2022 State Assessment

The following table presents the number of schools selected for the fourth- and eighth-grade public school mathematics and reading samples by sampling frame ( Common Core of Data [CCD]-based and new school) and participating jurisdiction. The school counts shown are at the time of sampling. In the table, the first column, Jurisdiction, is either the "state name" if the state does not have a Trial Urban District Assessments (TUDA) district (e.g., Alaska) or the "state name + TUDA district name" (e.g., California— Los Angeles) and "state name + non-TUDA part" (e.g., California—Balance).

After school sampling, some schools in TUDA districts were discovered to be charter schools that were the responsibility of the state and not the individual TUDA district. These schools were reclassified from TUDA to "balance of the state".

Number of schools in the total, CCD-based, and new-school samples, state assessment, by grade and region: 2022

Jurisdiction	Grade 4			Grade 8
Jurisdiction
Total school sample	CCD-based school sample	New-school sample	Total school sample	CCD-based school sample	New-school sample
Total	6,010	5,960	50	5,490	5,440	60
Alabama	90	90	#	90	90	#
Alaska	130	130	#	110	110	#
Arizona	90	90	#	90	90	#
Arkansas	90	90	#	90	90	#
California–Los Angeles	60	60	#	60	60	#
California–San Diego	40	40	#	40	40	#
California–Balance	80	80	#	80	80	#
Colorado–Denver	40	40	#	40	40	#
Colorado–Balance	80	80	#	80	80	#
Connecticut	90	90	#	90	90	#
Delaware	80	80	#	50	50	#
Florida–Duval County	40	40	#	40	30	#
Florida–Hillsborough County	40	40	#	40	40	#
Florida–Miami-Dade County	60	60	#	70	70	#
Florida–Balance	60	60	#	70	70	#
Georgia–Atlanta	40	40	#	30	30	#
Georgia–Balance	80	80	#	80	80	#
Hawaii	90	90	#	50	50	#
Idaho	90	90	#	90	90	#
Illinois–Chicago	70	70	#	70	70	#
Illinois–Balance	80	80	#	70	70	#
Indiana	90	90	#	90	90	#
Iowa	90	90	#	90	90	#
Kansas	100	100	#	90	90	#
Kentucky–Jefferson County	40	40	#	30	30	#
Kentucky–Balance	70	70	#	80	80	#
Louisiana	90	90	#	90	90	#
Maine	110	110	#	90	90	#
Maryland–Baltimore	50	50	#	50	50	#
# Rounds to zero.

Shape224

	Grade 4			Grade 8
Total school	CCD-based school	New-school	Total school	CCD-based school	New-school
sample	sample	sample	sample	sample	sample

Jurisdiction

Maryland–Balance	80	80	#	80	80	#
Massachusetts–Boston	50	50	#	50	50	#
Massachusetts–Balance	80	80	#	80	80	#
Michigan–Detroit	40	40	#	40	40	#
Michigan–Balance	90	90	#	90	90	#
Minnesota	90	90	#	100	90	#
Mississippi	90	90	#	90	90	#
Missouri	100	100	#	100	100	#
Montana	130	130	#	100	100	#
Nebraska	100	100	#	100	100	#
Nevada–Clark County	60	60	#	50	50	#
Nevada–Balance	30	30	#	30	30	#
New Hampshire	100	100	#	80	80	#
New Jersey	90	90	#	90	90	#
New Mexico–Albuquerque	40	40	#	40	30	#
New Mexico–Balance	70	70	#	70	70	#
New York–New York City	70	70	#	70	70	#
New York–Balance	60	60	#	60	60	#
North Carolina–Charlotte	40	40	#	30	30	#
North Carolina–Guilford County	40	40	#	30	30	#
North Carolina–Balance	80	70	#	80	80	#
North Dakota	120	120	#	90	90	#
Ohio–Cleveland	50	50	#	50	50	#
Ohio–Balance	90	90	#	90	90	#
Oklahoma	100	100	#	90	90	#
Oregon	90	90	#	90	90	#
Pennsylvania–Philadelphia	40	40	#	40	40	#
Pennsylvania–Balance	80	80	#	80	80	#
Rhode Island	90	90	#	60	60	#
South Carolina	90	90	#	90	90	#
South Dakota	120	120	#	100	100	#
Tennessee–Shelby County	40	40	#	40	40	#

# Rounds to zero.

Shape225

	Grade 4			Grade 8
Total school	CCD-based school	New-school	Total school	CCD-based school	New-school
sample	sample	sample	sample	sample	sample

Jurisdiction

Tennessee–Balance	80	80	#	80	80	#
Texas–Austin	40	40	#	20	20	#
Texas–Dallas	40	40	#	40	40	#
Texas–Fort Worth	40	40	#	30	30	#
Texas–Houston	60	60	#	40	40	#
Texas–Balance	80	80	#	80	80	#
Utah	90	90	#	90	90	#
Vermont	130	130	#	90	90	#
Virginia	90	80	#	90	80	#
Washington	90	90	#	90	90	#
West Virginia	100	100	#	90	90	#
Wisconsin–Milwaukee	50	50	#	40	40	#
Wisconsin–Balance	90	90	#	80	80	#
Wyoming	100	100	#	70	60	10
Other jurisdictions
Bureau of Indian Education (BIE)	10	10	#	10	10	#
Department of Defense Education Activity (DoDEA)	100	90	10	60	60	#
District of Columbia (TUDA)	50	50	#	30	30	#
District of Columbia–Balance	40	40	#	50	40	10
Puerto Rico	150	150	#	150	150	#

# Rounds to zero.

NOTE: Numbers of schools are rounded to nearest ten. Detail may not sum to totals due to rounding.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/school_sample_sizes_for_the_2022_state_assessment.aspx

Shape226

NAEP Technical Documentation Stratification of Schools for the 2022 State Assessment

The purpose of school stratification is to increase the efficiency and ensure the representativeness of the school samples in terms of important school-level characteristics, such as geography (e.g., states and TUDA districts), urbanicity, and race/ethnicity classification. NAEP school sampling utilizes two types of stratification: explicit and implicit.

Stratification Variables

Explicit stratification partitions the sampling frame into mutually exclusive groupings called strata. The systematic samples selected from these strata are independent, meaning that each is selected with its own unique random start. The explicit school strata for the 2022 NAEP state assessments were usually states. If a state contained Trial Urban District Assessment (TUDA) districts, the explicit strata were each individual TUDA district and the balance of the state. In 2022, there were 26 participating TUDA districts in the NAEP state assessment program. They are listed below:

Albuquerque Public Schools, New Mexico; Atlanta Public Schools, Georgia;

Austin Independent School District, Texas; Baltimore City Public Schools, Maryland; Boston Public Schools, Massachusetts;

Charlotte-Mecklenburg Schools, North Carolina; Chicago Public Schools, Illinois;

Clark County School District, Nevada;

Cleveland Metropolitan School District, Ohio; Dallas Independent School District, Texas;

Denver Public Schools, Colorado; Detroit Public Schools, Michigan;

District of Columbia Public Schools, District of Columbia; Duval County Public Schools, Florida;

Fort Worth Independent School District, Texas; Guilford County Schools, North Carolina;

Hillsborough County Public Schools, Florida; Houston Independent School District, Texas;

Jefferson County Public Schools (Louisville), Kentucky; Milwaukee Public Schools, Wisconsin;

Los Angeles Unified School District, California; Miami-Dade County Public Schools, Florida;

New York City Department of Education, New York; School District of Philadelphia, Pennsylvania;

San Diego Unified School District, California; and Shelby County Schools, Tennessee.

Implicit stratification involves sorting the sampling frame, as opposed to grouping the frame. For NAEP, schools are sorted by key school characteristics within explicit strata and sampled systematically using this ordering. This type of stratification ensures the representativeness of the school samples with respect to the key school characteristics. The implicit school stratification variables for the 2022 state assessments included urbanicity, race/ethnicity classification, achievement score/median income, and magnet school indicator. Further details about these variables can be found here.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_of_schools_for_the_2022_state_assessment.aspx

Shape231

NAEP Technical Documentation Stratification Variables for the 2022 State Assessment

The implicit stratification of public schools for the NAEP 2022 state assessments involved four dimensions:

urbanicity classification (urban-centric locale); race/ethnicity classification;

achievement data or median income; and magnet school indicator.

The urbanicity stratum is the top-level implicit stratification variable and is assigned within each explicit stratum. It is derived from the NCES urban-centric locale variable and classifies schools based on location (city, suburb, town, rural) and proximity to urbanized areas. It has 12 possible values.

The race/ethnicity stratum classifies schools by the relative magnitude of enrollment of non-Hispanic White, non-Hispanic Black,

Stratification by Urbanicity Classification

Stratification by Race/ethnicity Classification

Stratification by Achievement Data and Median Income

Missing Stratification Variables

Hispanic, Asian, American Indian/Alaska Native, Hawaiian/Pacific Islander, and students classified as two or more races represented in schools. The source of the race/ethnicity data is the Common Core of Data (CCD). The race/ethnicity stratum is the second-level variable in the stratification hierarchy and is nested within the urbanicity stratum.

The next stratification dimension is a classification of schools based on either achievement data or median household income. For most jurisdictions including TUDA districts, it is based on achievement data. However, not all jurisdictions provide achievement data. In these cases, median household income is used instead. Median income comes from 5-year estimates from the 2015–2019 American Community Survey (ACS), and it corresponds to the zip code area where the school is located.

The final stratification dimension indicates whether a school is classified as a magnet school or not, according to the CCD. It is used to provide an additional level of classification among the highest-achieving schools, to differentiate between high-achieving magnet schools and high-achieving non-magnet schools. Many domains do not classify any schools as magnet, in which case this variable has no effect on the implicit stratification.

Missing values for stratification variables were imputed.

The implicit stratification in this hierarchical procedure was achieved via a "serpentine sort" within a given explicit stratum. This sort was accomplished by alternating between ascending and descending sort order on each variable successively through the sort hierarchy. The following table shows an oversimplified example to illustrate the ascending- descending-ascending-descending pattern of the serpentine sort. Since the magnet school indicator was not applicable in most domains, it is omitted from the example table for simplicity.

Stratification variables sorted by serpentine sort: 2022

TUDA	Urbanicity	Race/ethnicity level	Achievement score
Yes	Large City	High minority	20
			22
			27
			30
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 State Mathematics and Reading Assessments.

TUDA Urbanicity Race/ethnicity level Achievement score

		Low minority	29
			26
			20
			18
	Mid-size City	Low minority	15
			25
			27
			31
		High minority	35
			32
			30
			28
No	Mid-size City	High minority	20
			22
			27
			30
		Low minority	29
			26
			20
			18
	Large City	Low minority	15
			25
			27
			31
		High minority	35
			32
			30
			28

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_variables_for_the_2022_state_assessment.aspx

NAEP Technical Documentation Missing Stratification Variables for the 2022 State Assessment

Schools with missing stratification variables had their data imputed as follows.

Schools missing the urbanicity (urban-centric locale) variable were assigned the modal value of urbanicity for schools in the same five-digit zip code or the same city. The modal value is the value that occurs the most. For example, one school in zip code 32305 has missing urbanicity. In the same five-digit zip code area, there are 20 schools with non-missing urbanicity variable. Fifteen of them have an urbanicity value of "mid-size city", and the other five have an urbanicity value of "large suburb". The modal value

of urbanicity for schools in zip code 32305 is "mid-size city".

The mean ethnicity percentage was imputed at the five-digit zip code level only if all schools were missing ethnicity at the district level, and only at the three-digit zip code prefix if the five-digit zip code ethnicity mean was missing as well. Thus, schools with missing or questionable values in race/ethnicity enrollment data—those in which the summation of the ethnicity percentages did not fall in the range 97 through 103, indicating a gross error—were assigned the average race/ethnicity enrollment within (in priority order) their school district, five-digit zip code, or three-digit zip code prefix.

Schools with missing achievement data in jurisdictions and grades for which achievement data were used in stratification were assigned the mean achievement data value within their urbanization and race/ethnicity classification. The achievement data were imputed only for those schools in jurisdictions and grades in which achievement data were used for stratification.

Schools missing median household income were assigned the mean value of median household income for the five-digit zip code prefix in which they were located. If it was not available or it was unreliable, then the mean value of median household income for the three-digit zip code prefix was used. In some cases, imputation was not possible at the three-digit zip code level, and needed to be done at the city and state level.

Schools with missing estimated grade enrollment had their estimated grade enrollment set to 20.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/missing_stratification_variables_for_the_2022_state_assessment.aspx

Shape233

NAEP Technical Documentation Stratification by Achievement Data and Median Income for the 2022 State Assessment

The achievement data obtained from each jurisdiction, including TUDA districts, are derived from the results of state assessment programs. The contents of the achievement data files varied by jurisdiction and included achievement measures for a variety of subjects, grades, and multiple assessment programs. One achievement measure was selected for each responding jurisdiction to be used in the stratification process. Where available, the achievement data were used for implicit stratification by grade. Since the achievement data are more current than the median household income data, as well as more likely to be well-correlated to NAEP assessment scores, they were judged to be a more effective stratification variable. The achievement measures were selected according to the following criteria:

At both grades 4 and 8, achievement measures from state assessments conducted in mathematics and reading were under consideration. If both were available, the mathematics measure was preferred. As a rule, the most current measures available were used. For all jurisdictions, the measures were from the 2018–2019 state

assessments.

Achievement measures should match to at least 70 percent of the schools on the sampling frames.

Achievement measures should differentiate schools from one another. For example, district-level measures or those with high missing rates (30 percent or more), were judged not to be useful for differentiating schools. In addition, achievement measures that did not have large enough dispersion, based on inspection, were not used for stratification either.

All other things being equal, the possibilities for score types were average scale score, median scale score, percentile rank, median percentile rank, normal curve equivalent, raw score, index score, and percentage above a particular cut point or quartile. In general, the availability varied for any given jurisdiction/grade/subject/year.

Achievement data used for implicit stratification were obtained for all 50 states and the District of Columbia for both fourth- and eighth-grade assessments. In Alaska where the match rate was too low, 2016–2017 state assessment data were used instead. In Puerto Rico where achievement data were not available, median household income was used based on the zip code area in which the school was located. The source of median household income for Puerto Rico was 5-year estimates from the 2015–2019 American Community Survey (ACS). The estimated grade enrollment was used for the stratification for DoDEA and BIE schools, since neither achievement data nor median income were available. Estimated grade enrollment was obtained from the Common Core of Data (CCD) file developed by NCES.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_by_achievement_data_and_median_income_for_the_2022_state_assessment.aspx

NAEP Technical Documentation Stratification by Race/Ethnicity Classification for the 2022 State Assessment

Race/ethnicity classification was based on the second and third largest race/ethnicity percentages (among non-Hispanic White, non-Hispanic Black, Hispanic, Asian, American Indian/Alaska Native, Native Hawaiian/Pacific Islander, and students classified as two or more races) within each urbanicity classification stratum. The race/ethnicity strata were formed using one of three classification schemes as follows:

Case 1: Urbanicity cells where both the second and third largest race/ethnicity groups contained less than 7 percent of students in the urbanicity cell were not stratified by race/ethnicity enrollment (race/ethnicity stratification value was set to 0). There were no race/ethnicity strata formed within these urbanicity cells.

Case 2: Urbanicity cells where the second largest race/ethnicity group contained at least 7 percent but the second and third largest race/ethnicity groups combined contained no more than 15 percent of students in the urbanicity cell were stratified into three race/ethnicity cells. Schools were ordered by the sum of the percentage of race/ethnicity enrollment for the second and third largest groups within the urbanicity cell and then divided into three approximately equal size groups in terms of students.

Case 3: Urbanicity cells where both the second and third largest race/ethnicity groups contained more than 15 percent of students in the urbanicity cell were stratified into four race/ethnicity cells. The second largest group provided the primary stratification variable; the third largest group provided the secondary stratification variable.

Within an urbanicity cell, schools were first sorted based on the primary stratification variable. Then they were divided into two strata of schools containing approximately equal numbers of students. Within each of these two strata, the schools were sorted by the secondary stratification variable and subdivided into two substrata of schools containing approximately equal numbers of students. The four race/ethnicity classifications consisted of the following values: low primary

variable/low secondary variable, low primary variable/high secondary variable, high primary variable/low secondary variable, and high primary variable/high secondary variable.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_by_race_ethnicity_classification_for_the_2022_state_assessment.aspx

NAEP Technical Documentation Stratification by Urbanicity Classification for the 2022 State Assessment

The creation of the urbanicity classification variable was based on the NCES urban-centric locale and was defined within each explicit stratum. The NCES urban-centric locale contains the following categories:

Large City: Territory inside an urbanized area and inside a principal city with a population of 250,000 or more;

Mid-size City: Territory inside an urbanized area and inside a principal city with a population less than 250,000 and greater than or equal to 100,000; Small City: Territory inside an urbanized area and inside a principal city with a population less than 100,000;

Large Suburb: Territory outside a principal city and inside an urbanized area with a population of 250,000 or more;

Mid-size Suburb: Territory outside a principal city and inside an urbanized area with a population less than 250,000 and greater than or equal to 100,000; Small Suburb: Territory outside a principal city and inside an urbanized area with a population less than 100,000;

Fringe Town: Territory inside an urban cluster that is less than or equal to 10 miles from an urbanized area;

Distant Town: Territory inside an urban cluster that is more than 10 miles and less than or equal to 35 miles from an urbanized area; Remote Town: Territory inside an urban cluster that is more than 35 miles from an urbanized area;

Fringe Rural: Census-defined rural territory that is less than or equal to 5 miles from an urbanized area, as well as rural territory that is less than or equal to 2.5 miles from an urban cluster;

Distant Rural: Census-defined rural territory that is more than 5 miles but less than or equal to 25 miles from an urbanized area, as well as rural territory that is more than

2.5 miles but less than or equal to 10 miles from an urban cluster; and

Remote Rural: Census-defined rural territory that is more than 25 miles from an urbanized area and is also more than 10 miles from an urban cluster.

In addition to the 12 categories above, the category "outside of the United States: Department of Defense Education Activity (DoDEA) overseas schools or Puerto Rico" is used. For the definitions of the geographic terms used in these descriptions, please refer to the Census Bureau’s website (for example, www.census.gov/programs- surveys/metro-micro.html).

The urbanicity classification cells were created by starting with the original NCES urban-centric locale categories. Urbanicity strata were collapsed with neighboring strata until a minimum cell size criterion, in terms of the percentage of students, was met. The minimum cell size criterion varied by type of explicit stratum. The criterion for explicit strata comprising the largest TUDA districts (Los Angeles, New York City, Chicago, Miami-Dade, Houston, and Clark County) was 13 percent; for the other TUDA districts, it was 20 percent; and for all other explicit strata, it was 10 percent.

The urbanicity classification variable was equal to the original NCES urban-centric locale if no collapsing was necessary. If collapsing was necessary, the collapsing scheme first collapsed within the four major strata (city, suburbs, town, rural). For example, urbanicity categories 1, 2, and 3 within city were collapsed (1 with 2, 2 with 3) if cells 1 or 3 were deficient. If the middle cell (e.g., 2) was deficient, then it was collapsed with the smaller of the two end cells. If a collapsed pair was still deficient, it was collapsed with the remaining unit within the major stratum. That is, a single city cell would be created by collapsing the large city, mid-size city, and small city cells. If a cell was still deficient after collapsing within major stratum, further collapsing across major strata occurred as needed until the deficiency was resolved. The values of the urbanicity classification variable were set equal to the cell value of the final level of collapsing.

Prior experience with this type of stratification has shown that the greatest efficiency of stratification results when cities and suburb areas are always kept separate from towns and rural areas, even if the enrollment criterion is violated.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/stratification_by_urbanicity_classification_for_the_2022_state_assessment.aspx

Shape236

NAEP Technical Documentation Student Sample Selection for the 2022 State Assessment

The sampling of students for the state assessments in mathematics and reading involved two steps: (1) sampling of students in the targeted grade (fourth or eighth) from each sampled school, and (2) assignment of assessment subject (mathematics or reading) to the sampled students.

Sampling Students within Sampled Schools

Within each sampled school, a sample of students was selected from a list of students in the targeted grade such that every student had an equal chance of selection. The student lists were submitted either electronically using a system known as E-filing or on paper. In E-filing, student lists are submitted as Excel files by either school coordinators, NAEP State Coordinators, or NAEP TUDA Coordinators. The files can be submitted for one school at a time (known as single school E-file submission) or for an entire jurisdiction at once (known as multiple school E-file submission). E-filing allows schools to easily submit student demographic data electronically with the student lists, easing the burden on field supervisors and school coordinators.

Schools that are unable to submit their student lists using the E-filing system provide hardcopy lists to field supervisors. In 2022, across all state assessment samples combined, over 99 percent of the participating schools E-filed their student lists while less than 1 percent of the participating schools submitted hardcopy lists.

The sampling process was the same, regardless of list submission type. The sampling process was systematic (e.g., if the sampling rate was one-half, a random starting point of one or two was chosen, and every other student on the list was selected). For E-filed schools only, where demographic data was submitted for every student on the frame, students were sorted by gender and race/ethnicity before the sample was selected to implicitly stratify the sample.

In some jurisdictions, every student in the targeted grade was needed to meet the overall student sample size. In these jurisdictions, all students in all schools at the targeted grade were sampled.

In the other jurisdictions except for Puerto Rico, in schools with up to 52 students in the targeted grade, all students were selected. In schools with more than 52 students, systematic samples of 50 students were selected. In some cases, a larger school may have been selected with certainty during the school sample selection process, and thus may have selected more students.

For Puerto Rico, in schools with up to 26 students in the targeted grade, all students were selected. In schools with more than 26 students, systematic samples of 25 students were selected.

Some students enrolled in the school after the sample was selected. In such cases, new enrollees were sampled at the same rate as the students on the original list.

Assigning Assessment Subject to Sampled Students

In all jurisdictions except Puerto Rico, sampled students including new enrollees in each participating sampled school were assigned to either the mathematics or the reading assessment at rates of 52 percent and 48 percent, respectively, for grade 4; or 50 percent for each subject for grade 8, using a process known as spiraling. In this process, test forms were randomly assigned to sampled students from test form sets that had, on average, a ratio of 26 mathematics forms to 24 reading forms for grade 4, and a ratio of 25 mathematics forms to 25 reading forms for grade 8. Students receiving a mathematics form were in the mathematics assessment, and students receiving a reading form were in the reading assessment. For Puerto Rico, all students were assigned a mathematics form since it was only participating in the operational mathematics assessment.

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/student_sample_selection_for_the_2022_state_assessment.aspx

Shape237

NAEP Technical Documentation Target Population for the 2022 State Assessment

The target population for the 2022 fourth- and eighth-grade public school state assessments in mathematics and reading was defined as all fourth- and eighth-grade students who were enrolled in public schools located in the 50 states, the District of Columbia, and Puerto Rico, Bureau of Indian Education (BIE) schools, and Department of Defense Education Activity (DoDEA) schools (including those located outside the United States).

http://nces.ed.gov/nationsreportcard/tdw/sample_design/2022/target_population_for_the_2022_state_assessment.aspx

Shape238

NAEP Technical Documentation Weighting Procedures for the 2022 Assessment

NAEP assessments use complex sample designs to create student samples that generate population and subpopulation estimates with reasonably high precision. School and student sampling weights ensure valid inferences from the student samples to their respective populations. In 2022, weights were developed for schools and students sampled at grades 4 and 8 for assessments in

Computation of Full-Sample Student Weights

mathematics and reading, schools and students sampled at grade 8 for assessments in civics and U.S. history, and for schools and students sampled at ages 9 and 13 for long-term trend (LTT) assessments in mathematics and reading. The grade-based assessments were administered using tablets, and the LTT assessments were administered using paper and pencil.

Student Weights

Each student was assigned a weight to be used for making inferences about students in the target population. This weight is known as the final full-sample student weight and contains the following major components:

the student base weight,

school nonresponse adjustments, student nonresponse adjustments,

school weight trimming adjustments,

student weight trimming adjustments, and student raking adjustment.

Computation of Replicate Student Weights for Variance Estimation

Computation of Full-Sample School Weights

Computation of Replicate School Weights for Variance Estimation

Quality Control on Weighting Procedures

The student base weight is the inverse of the overall probability of selecting a student and assigning that student to a particular assessment. The sample design that determines the base weights is discussed in the NAEP 2022 Sample Design section.

The student base weight is adjusted for two sources of nonparticipation: at the school level and at the student level. These weighting adjustments seek to reduce the potential for bias from such nonparticipation. Responding schools receive a weighting adjustment to compensate for nonresponding schools, and responding students receive a weighting adjustment to compensate for nonresponding students.

Furthermore, the final weights reflect the trimming of extremely large weights at both the school and student level. These weighting adjustments seek to reduce variances of survey estimates.

An additional weighting adjustment was implemented in the state and Trial Urban District Assessment (TUDA) samples so that estimates for key student-level characteristics were in agreement across assessments in reading and mathematics. This adjustment was implemented using a raking procedure. A similar but separate adjustment was also implemented for the national public school civics and U.S. history samples at grade 8. The raking procedure implemented for civics and U.S. history brought estimates for key student-level characteristics into agreement with those from mathematics and reading at the national level. Similar to previous years, raking was not performed for any of the private school student samples or for student samples in the LTT assessments.

In addition to the final full-sample weight, a set of replicate weights was provided for each student. These replicate weights are used to calculate the variances of survey estimates using the jackknife repeated replication method. The methods used to derive these weights were aimed at reflecting the features of the sample design, so that when the jackknife variance estimation procedure is implemented, approximately unbiased estimates of sampling variance are obtained. In addition, the various weighting procedures were repeated on each set of replicate weights to appropriately reflect the impact of the weighting adjustments on the sampling variance of a survey estimate. A finite population correction (fpc) factor was incorporated into the replication scheme so that it could be reflected in the variance estimates for the grade-based assessments. Similar to previous years, the replication scheme for LTT does not incorporate a finite population correction factor. See Computation of Replicate Student Weights for Variance Estimation for details.

School Weights

In addition to student weights, school weights were calculated to provide secondary users means to analyze data at the school level. The school weights are subject specific and represent the schools that contained at least one student that participated in the NAEP assessment for that subject.

Each school was assigned a weight to be used for making inferences about schools in the target population. This weight is known as the final full-sample school weight, and it contains five major components:

the school base weight,

school nonresponse adjustment,

school weight trimming adjustment,

school session assignment weight, and small-school subject adjustment.

The school base weight is the inverse of the probability of selecting a school for a particular assessment. The school nonresponse adjustment increase the weights of participating schools to account for similar schools that did not participate, and the school trimming adjustment reduce extremely large weights to decrease variances of survey estimates. These two adjustments are the same school-level adjustments used in the student full-sample weight described above.

The school session assignment weight reflects the probability that the particular session type was assigned to the school.

The small-school subject adjustment accounts for very small schools that did not have enough participating students for every subject associated to the school. School weights for subjects that had at least one eligible student are inflated by this factor to compensate for subject(s) that did not have any eligible students in that school and, thus, are not represented otherwise. In addition to the full-sample weight, a set of replicate weights was provided for each school. The school replicate weights are used to calculate the variances of school-level survey estimates using the jackknife repeated replication method.

Quality Control Procedures

Quality control checks were carried out throughout the weighting process to ensure the accuracy of the full-sample and replicate weights. See Quality Control on Weighting Procedures for the various checks implemented and main findings of interest.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/weighting_procedures_for_the_2022_assessment.aspx

Shape239

NAEP Technical Documentation Computation of Full-Sample School Weights

The full-sample or final school weight is the sampling weight used to derive NAEP school estimates of population and subpopulation characteristics for a specified grade (4 and 8) or age (9) and assessment subject (civics, mathematics, reading, and U.S. history). The full-sample school weight reflects the number of schools that the sampled school represents in the population for purposes of estimation.

The full-sample weight, which is used to produce survey estimates, is distinct from a replicate weight that is used to estimate variances of survey estimates. The full-sample weight is assigned to participating schools and reflects the school base weight after the application of the various weighting adjustments. The full-sample weight \ (SCH\_WGT_{js}\) for school $s$ in stratum $j$ can be expressed as follows:

\begin{equation} SCH\_WGT_{js} = SCH\_BWT_{js} \times SCH\_NRAF_{js} \times SCH\_TRIM_{js} \times SCHSESWT_{js} \times SCH\_SUBJ\_AF_{js}

\end{equation} where

Shape240 $SCH\_BWT_{js}$ is the school base weight;

Shape241 $SCH\_NRAF_{js}$ is the school-level nonresponse adjustment factor;

Shape242 $SCH\_TRIM_{js}$ is the school-level weight trimming adjustment factor;

$SCHSESWT_{js}$ is the school-level session assignment weight that reflects the conditional probability, given the school, that the particular session type was assigned to the school; and

$SCH\_SUBJ\_AF_{js}$ is the small-school subject adjustment factor.

For 2022, the school-level session assignment weight is always one because schools were only assigned to one session type.

The small-school subject adjustment accounts for very small schools that did not have enough participating students for every subject intended for the school. School weights for subjects that had at least one eligible student are inflated by this factor to compensate for schools of the same size that did not have any eligible students for those subjects and would not be represented otherwise.

The factor is equal to the inverse of the probability that a school of a given size had at least one eligible sampled student in a given subject:

\begin{equation} SCH\_SUBJ\_AF_{js} = \max \biggl(\dfrac{SF_{js}}{n_{s}},1 \biggr) \end{equation}

where

Shape243
Shape244

$SF_{js}$ is the spiraling factor for the given subject; and

$n_{s}$ is the within-school student sample size.

For example, if a school was to assess students in two subjects with a spiraling ratio of 1:1 (i.e., a spiraling factor of 2) but had only one eligible student, then the small-school subject adjustment would be equal to 2. The factor for schools not needing this adjustment was set equal to 1.

For the 2022 operational assessments, schools could be assigned to one of four sample types:

Grades 4 and 8 mathematics and reading except Puerto Rico,
Grade 8 civics and U.S. history,
Grades 4 and 8 mathematics (Puerto Rico),
Age 9 mathematics and reading long-term trend (LTT).

Students in schools participating in the grades 4 and 8 mathematics and reading assessments were assigned to mathematics and reading at the rates of 52 percent and 48 percent respectively at grade 4, and 50 percent for each subject at grade 8. Students in schools participating in the grade 8 civics and U.S. history assessments were assigned to civics and U.S. history at the rates of 49 percent and 51 percent respectively. Students in schools participating in the age 9 mathematics and reading assessments were assigned to mathematics and reading at rates of 50 percent for each subject. Puerto Rico had only one operational assessment, so all students in grades 4 and 8 assigned to the operational assessment were assigned to mathematics.

Overall, the school weights of 27 of the approximately 5,200 schools participating in the grade 4 mathematics and reading assessment sample were adjusted to compensate for schools that were too small to take part only in mathematics or only in reading. The small-school adjustment factors ranged from 1.03 to 2.07. For the grade 8 mathematics and reading assessment sample, seven of 5,200 schools had their school weights adjusted to compensate for their size. The small-school adjustment factor was 2.00. Only one out of 400 schools had its school weight adjusted for the LTT assessments in mathematics and reading to account for schools that were too small to participate in both subjects. The small-school adjustment factor of 2 was used. For the assessment sample in civics and U.S. history at grade 8, the adjustment factor was set equal to 1 for all schools.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computation_of_full_sample_school_weights_for_the_2022_assessment.aspx

Shape245

NAEP Technical Documentation Computation of Full-Sample Student Weights

The full-sample or final student weight is the sampling weight used to derive NAEP student estimates of population and subpopulation characteristics for a specified grade (4 or 8) or age (9 or 13) and assessment subject (civics,

mathematics, reading, or U.S. history). The full-sample student weight reflects the number of students in the population that the sampled student represents for purposes of estimation. The summation of the final student weights over a particular student group provides an estimate of the total number of students in that group within the population.

The full-sample weight, which is used to produce survey estimates, is distinct from a replicate weight that is used to estimate variances of survey estimates. The full-sample weight is assigned to participating students and reflects the student base weight after the application of the various weighting adjustments. The full-sample weight $FSTUWGT_{jsk}$ for student $k$ from school $s$ in stratum $j$ can be expressed as

Computation of Base Weights

School and Student Nonresponse Weight Adjustments

School and Student Weight Trimming Adjustments

Student Weight Raking Adjustment

\begin{equation} FSTUWGT_{jsk} = STU\_BWT_{jsk} \times SCH\_NRAF_{js} \times STU\_NRAF_{jsk} \times \\ SCH\_TRIM_{js} \times STU\_TRIM_{jsk} \times STU\_RAKE_{jsk} , \end{equation}

where

$STU\_BWT_{jsk}$ is the student base weight;

$SCH\_NRAF_{js}$ is the school-level nonresponse adjustment factor;

$STU\_NRAF_{jsk}$ is the student-level nonresponse adjustment factor;

$SCH\_TRIM_{js}$ is the school-level weight trimming adjustment factor;

$STU\_TRIM_{jsk}$ is the student-level weight trimming adjustment factor; and $STU\_RAKE_{jsk}$ is the student-level raking adjustment factor.

School sampling strata for a given assessment vary by school type (public or private), assessment subject (civics, mathematics, reading, or U.S. history), and grade (4 or 8) or age (9 or 13). See the links below for descriptions of the school strata for the various assessments.

State public school samples for mathematics and reading at grades 4 and 8

National private school samples for mathematics and reading at grades 4 and 8 National public school samples for civics and U.S. history at grade 8

National private school samples for civics and U.S. history at grade 8

National public school samples for mathematics and reading at ages 9 and 13 National private school samples for mathematics and reading at ages 9 and 13

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computation_of_full_sample_student_weights_for_the_2022_assessment.aspx

NAEP Technical Documentation Computation of Base Weights

Every sampled school and student received a base weight equal to the reciprocal of its probability of selection. Computation of a school base weight varies by

type of sampled school (original or substitute); and sampling frame (new school frame or not).

Computation of a student base weight reflects

the student's overall probability of selection accounting for school and student sampling; assignment to session type at the school- and student-level; and

the student's assignment to a particular subject.

School Base Weights Student Base Weights

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computation_of_base_weights_for_the_2022_assessment.aspx

NAEP Technical Documentation School Base Weights

The school base weight for a sampled school is equal to the inverse of its overall probability of selection. The overall selection probability of a sampled school differs by the type of sampled school (original or substitute) and by the type of sampling frame (new school frame or not).

The overall selection probability of an originally selected school in a civics, mathematics, reading, or U.S. history sample is equal to its probability of selection from the NAEP public/private school frame.

The overall selection probability of a school from the new school frame in a civics, mathematics, reading, or U.S. history sample is the product of two quantities:

the probability of selection of the school's district into the new-school district sample or the Catholic diocese into the new-school Catholic diocese sample, and the probability of selection of the school into the new school sample.

The new-school district sampling procedures for the 2022 national public school samples for the civics and U.S. history assessment at grade 8 are very similar to the new- school district sampling procedures for the 2022 state public schools assessments in mathematics and reading.

New-school Catholic diocese sampling procedures for the 2022 national private school assessments for mathematics and reading at grades 4 and 8 and for civics and U.S. history at grade 8 are similar as well.

For the mathematics and reading long-term trend (LTT) assessments at ages 9 and 13, the new-school district and Catholic diocese sampling procedures took advantage of the work already being done for the grade-based assessments.

Substitute schools are preassigned to original schools and take the place of original schools if they refuse to participate. For weighting purposes, substitute schools are treated as if they were the original schools they replaced, so substitute schools are assigned the school base weight of their corresponding original schools.

Learn more about substitute schools for the 2022 national public school assessments for civics and U.S. history at grade 8 and for mathematics and reading LTT assessments at age 9. The 2022 state public school assessment in mathematics and reading do not use substitute schools.

Learn more about substitute schools for the 2022 national private school assessments in mathematics and reading at grades 4 and 8, in civics and U.S. history at grade 8, and in mathematics and reading LTT assessments at ages 9 and 13.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/school_base_weights_for_the_2022_assessment.aspx

Shape248

NAEP Technical Documentation Student Base Weights

Every sampled student received a student base weight, whether or not the student participated in the assessment. The student base weight is the reciprocal of the probability that the student was sampled to participate in the assessment for a specified subject. The student base weight $STU\_BWT_{jsk}$ for student $k$ from school $s$ in stratum $j$ is the product of seven weighting components and can be expressed as

\begin{equation} STU\_BWT_{jsk} = SCH\_BWT_{js} \times SCHSESWT_{js} \times WINSCHWT_{js} \times \\ STUSESWT_{jsk} \times SUBJFAC_{jsk} \times SUBADJ_{js} \times YRRND\_AF_{js}, \end{equation}

where

$SCH\_BWT_{js}$ is the school base weight;

$SCHSESWT_{js}$ is the school-level session assignment weight that reflects the conditional probability, given the school, that the particular session type was assigned to the school;

$WINSCHWT_{js}$ is the within-school student weight that reflects the conditional probability, given the school, that the student was selected for the NAEP assessment;

$STUSESWT_{jsk}$ is the student-level session assignment weight that reflects the conditional probability, given that the particular session type was assigned to the school, that the student was assigned to the session type;

$SUBJFAC_{jsk}$ is Stu_factor the subject spiral adjustment factor that reflects the conditional probability, given that the student was assigned to a particular session type, that the student was assigned the specified subject;

$SUBADJ_{js}$ is the substitution adjustment factor to account for the difference in enrollment size between the substitute and original school; and

$YRRND\_AF_{js}$ is the year-round adjustment factor to account for students in year-round schools on scheduled break at the time of the NAEP assessment and thus not available to be included in the sample.

The within-school student weight $(WINSCHWT_{js})$ is the inverse of the student sampling rate in the school. For long-term trend (LTT), due to the oversampling of certain race/ethnicity student groups, some schools have two student sampling rates.

The subject spiral adjustment factor $(SUBJFAC_{jsk})$ adjusts the student weight to account for the spiral pattern used in distributing civics, mathematics, reading, or

U.S. history booklets to the students. The subject factor varies by grade (or age, for LTT) and subject; it is equal to the inverse of the booklet proportions (civics, mathematics, reading, or U.S. history) in the overall spiral for a specific sample.

For cooperating substitutes of nonresponding original sampled schools, the substitution adjustment factor $(SUBADJ_{js})$ is equal to the ratio of the estimated grade (or age-specific) enrollment for the original sampled school to the estimated grade (or age-specific) enrollment for the substitute school. The student sample from the substitute school then "represents" the set of grade-eligible (or age-eligible) students from the original sampled school.

The year-round adjustment factor $(YRRND\_AF_{js})$ adjusts the student weight for students in year-round schools who do not attend school during the time of the assessment. This situation typically arises in overcrowded schools. School administrators in year-round schools randomly assign students to portions of the year in which they attend school and portions of the year in which they do not attend. At the time of assessment, a certain percentage of students (designated as $OFF_{js}$) do not attend school and thus cannot be assessed. The $YRRND\_AF_{js}$ for a school is calculated as $1/(1 - OFF_{js}/100)$.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/student_base_weights_for_the_2022_assessment.aspx

NAEP Technical Documentation School and Student Nonresponse Weight Adjustments

Nonresponse is unavoidable in any voluntary survey of a human population. Nonresponse leads to the loss of sample data that must be compensated for in the weights of the responding sample members. This differs from ineligibility, for which no adjustments are necessary. The purpose of the nonresponse adjustments is to reduce the mean square error of survey estimates. While the nonresponse adjustment reduces the bias from the loss of sample, it also increases variability among the survey weights leading to increased variances of the sample estimates. However, it is presumed that the reduction in bias more than compensates for the increase in the variance, thereby reducing the mean square error and thus improving the accuracy of survey estimates. Nonresponse adjustments are made in the NAEP surveys at both the school and the student levels: the responding (original and substitute) schools receive a weighting adjustment to compensate for nonresponding schools, and responding students receive a weighting adjustment to compensate for nonresponding students.

School Nonresponse Weight Adjustment

Student Nonresponse Weight Adjustment

The paradigm used for nonresponse adjustment in NAEP is the quasi-randomization approach (Oh and Scheuren, 1983). In this approach, school response cells are based on characteristics of schools known to be related to both response propensity and achievement level, such as the locale type (e.g., large principal city of a metropolitan area) of the school. Likewise, student response cells are based on characteristics of the schools containing the students and student characteristics that are known to be related to both response propensity and achievement level, such as student race/ethnicity, gender, and age.

Under this approach, sample members are assigned to mutually exclusive and exhaustive response cells based on predetermined characteristics. A nonresponse adjustment factor is calculated for each cell as the ratio of the sum of adjusted base weights for all eligible units to the sum of adjusted base weights for all responding units. The nonresponse adjustment factor is then applied to the base weight of each responding unit. In this way, the weights of responding units in the cell are "weighted up" to represent the full set of responding and nonresponding units in the response cell.

The quasi-randomization paradigm views nonresponse as another stage of sampling. Within each nonresponse cell, the paradigm assumes that the responding sample units are a simple random sample from the total set of all sample units. If this model is valid, then the use of the quasi-randomization weighting adjustment will eliminate any nonresponse bias. Even if this model is not valid, the weighting adjustments can eliminate bias if the achievement scores are homogeneous within the response cells. See, for example, chapter 4 of Little and Rubin (1987).

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/school_and_student_nonresponse_weight_adjustments_for_the_2022_assessment.aspx

Shape250

NAEP Technical Documentation School Nonresponse Weight Adjustment

The school nonresponse adjustment procedure inflates the weights of cooperating schools to account for eligible noncooperating schools for which no substitute schools participated. The adjustments are computed within nonresponse cells and are based on the assumption that the cooperating and noncooperating schools within the same cell are more similar to each other than to schools from different cells.

School nonresponse adjustments were carried out separately by sample; that is, by

sample level (state, national), school type (public, private),

grade (4, 8) or age (9, 13), and

assessment subject (civics, mathematics, reading, U.S. history).

Development of Initial School Nonresponse Cells

Development of Final School Nonresponse Cells

School Nonresponse Adjustment Factor Calculation

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/school_nonresponse_weight_adjustment_for_the_2022_assessment.aspx

Shape251

NAEP Technical Documentation Development of Final School Nonresponse Cells

Limits were placed on the magnitude of cell sizes and adjustment factors to prevent unstable nonresponse adjustments and unacceptably large nonresponse factors. All initial weighting cells with fewer than six cooperating schools or adjustment factors greater than 3.0 (or 4.0 for long-term trend [LTT]) for the full sample weight were collapsed with suitable adjacent cells. Simultaneously, all initial weighting cells for any replicate with fewer than four cooperating schools or adjustment factors greater than the maximum of

3.0 or two times the full sample nonresponse adjustment factor were collapsed with suitable adjacent cells. Initial weighting cells were generally collapsed in reverse order of the cell structure; that is, starting at the bottom of the nesting structure and working up toward the top level of the nesting structure.

State Public School Samples for Mathematics and Reading Assessments at Grades 4 and 8

For the grade 4 and 8 public school samples for mathematics and reading, cells with the most similar Black/Hispanic, achievement level, median income, or enrollment composition stratum within a given jurisdiction/Trial Urban District Assessment (TUDA) district and urbanicity (urban-centric locale) stratum were collapsed first. If further collapsing was required after all levels of the first variable were collapsed, cells with the most similar urbanicity strata were combined next. Cells were never permitted to be collapsed across jurisdictions or TUDA districts.

National Public School Samples for Civics and U.S. History Assessments at Grade 8

For the grade 8 public school civics and U.S. history sample, Black/Hispanic composition stratum cells within a given census division stratum and urbanicity stratum were collapsed first. If further collapsing was required after all levels of race/ethnicity classification were collapsed, cells with the most similar urbanicity strata were combined next. Any further collapsing occurred across census division strata but never across census regions.

National Public School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

For the LTT public school samples for mathematics and reading, race/ethnicity classification cells within a given census region stratum and urbanicity stratum were collapsed first. Any further collapsing occurred across urbanicity strata but never across census regions.

National Private School Samples for Mathematics and Reading Assessments at Grades 4 and 8

For the grade 4 and 8 private school samples for mathematics and reading, cells with the most similar race/ethnicity classification within a given affiliation, census region, and urbanicity stratum were collapsed first. If further collapsing was required after all levels of race/ethnicity strata were collapsed, cells with the most similar urbanicity classification were combined. Any further collapsing occurred across census region strata but never across affiliations.

National Private School Samples for Civics and U.S. History Assessments at Grade 8

For the grade 8 private school civics and U.S. history samples, cells with the most similar race/ethnicity classification within a given affiliation, census region, and urbanicity stratum were collapsed first. If further collapsing was required after all levels of race/ethnicity strata were collapsed, cells with the most similar urbanicity classification were combined. Any further collapsing occurred across census region strata but never across affiliations.

National Private School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

For the LTT private school samples for mathematics and reading, urbanicity strata within a given affiliation and census region were collapsed first. Any further collapsing occurred across census region strata but never across affiliations.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/development_of_final_school_nonresponse_cells_for_the_2022_assessment.aspx

Shape252

NAEP Technical Documentation Development of Initial School Nonresponse Cells

The cells for nonresponse adjustments are generally functions of the school sampling strata for the individual samples. School sampling strata usually differ by assessment subject, grade (or age for long-term trend [LTT]), and school type (public or private). Assessment subjects that are administered together by way of spiraling have the same school samples and stratification schemes. Subjects that are not spiraled with any other subjects have their own separate school sample. In NAEP 2022, the following assessments were spiraled together:

mathematics and reading assessments at grades 4 and 8; civics and U.S. history assessments at grade 8; and

mathematics and reading LTT assessments at ages 9 and 13.

The initial nonresponse cells for the various NAEP 2022 samples are described below.

State Public School Samples for Mathematics and Reading Assessments at Grades 4 and 8

For these samples, initial weighting cells were formed within each jurisdiction and grade using the following nesting cell structure:

Trial Urban District Assessment (TUDA) district vs. the balance of the state for states with TUDA districts; urbanicity (urban-centric locale) stratum; and

race/ethnicity classification stratum, achievement level, median income, or grade enrollment.

In general, the nonresponse cell structure used race/ethnicity classification stratum as the lowest level variable. However, where there was only one race/ethnicity classification stratum within a particular urbanicity stratum, then categorized achievement, median income, or enrollment data was used instead.

National Public School Samples for Civics and U.S. History Assessments at Grade 8 The initial weighting cells for these samples were formed using the following nesting cell structure:

census division stratum;

urbanicity stratum (urban-centric locale); and Black/Hispanic composition stratum.

National Public School Sample for Mathematics and Reading LTT Assessments at Ages 9 and 13

The initial weighting cells for these samples were formed using the following nesting cell structure:

census division stratum;

urbanicity stratum (four categories based on urban-centric locale); and

race/ethnicity classification (categories based on the total percentage of Black, Hispanic, and American Indian/Alaska Native students).

National Private School Samples for Mathematics and Reading Assessments at Grades 4 and 8

The initial weighting cells for these samples were formed within each grade using the following nesting cell structure:

affiliation;

census region stratum;

urbanicity stratum (urban-centric locale); and race/ethnicity classification stratum.

National Private School Samples for Civics and U.S. History Assessments at Grade 8 The initial weighting cells for these samples were formed using the following nesting cell structure:

affiliation;

census region stratum;

urbanicity stratum (urban-centric locale); and race/ethnicity classification stratum.

National Private School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

The initial weighting cells for these samples were formed using the following nesting cell structure:

affiliation;

census region stratum; and

urbanicity stratum (four categories based on urban-centric locale.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/development_of_initial_school_nonresponse_cells_for_the_2022_assessment.aspx

NAEP Technical Documentation School Nonresponse Adjustment Factor Calculation

In each final school nonresponse adjustment cell $c$, the school nonresponse adjustment factor $SCH\_NRAF_{c}$ was computed as

\begin{equation} SCH\_NRAF_{c} = \dfrac { \sum_{ s \in S_{c}} { SCH\_BWT_{s} \times SCH\_TRIM_{s} \times SCHSESWT_{s} \times X_{s}} } { \sum_{ s \in R_{c}}

{ SCH\_BWT_{s} \times SCH\_TRIM_{s} \times SCHSESWT_{s} \times X_{s}} }, \end{equation} where

$S_{c}$ is the set of all eligible sampled schools (cooperating original and substitute schools and refusing original schools with noncooperating or no assigned substitute) in cell $c$,

$R_{c}$ is the set of all cooperating schools within $S_{c}$, $SCH\_BWT_{s}$ is the school base weight,

$SCH\_TRIM_{s}$ is the school-level weight trimming factor,

$SCHSESWT_{s}$ is the school-level session assignment weight that reflects the conditional probability, given the school, that the particular assessment type was assigned to the school, and

$X_{s}$ is the estimated grade enrollment (or age-specific enrollment for long-term trend [LTT]) corresponding to the original sampled school.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/school_nonresponse_adjustment_factor_calculation_for_the_2022_assessment.aspx

Shape254

NAEP Technical Documentation Student Nonresponse Weight Adjustment

The student nonresponse adjustment procedure inflates the weights of assessed students to account for eligible sampled students who did not participate in the assessment. These inflation factors offset the loss of data associated with absent students. The adjustments are computed within nonresponse cells and are based on the assumption that the assessed and absent students within the same cell are more similar to one another than to students from different cells. Like its counterpart at the school level, the student nonresponse adjustment is intended to reduce the mean square error and thus improve the accuracy of NAEP assessment estimates. Also, like their counterparts at the school level, student nonresponse adjustments were carried out separately by sample; that is, by

grade (4, 8) or age (9, 13),

school type (public, private), and

assessment subject (civics, mathematics, reading, U.S. history).

Development of Initial Student Nonresponse Cells

Development of Final Student Nonresponse Cells

Student Nonresponse Adjustment Factor Calculation

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/student_nonresponse_weight_adjustment_for_the_2022_assessment.aspx

NAEP Technical Documentation Development of Final Student Nonresponse Cells

Similar to the school nonresponse adjustment, cell and adjustment factor size constraints are in place to prevent unstable nonresponse adjustments or unacceptably large adjustment factors. All initial weighting cells with either fewer than 20 participating students or adjustment factors greater than 2.0 for the full sample weight were collapsed with suitable adjacent cells. Simultaneously, all initial weighting cells for any replicate with either fewer than 15 participating students or an adjustment factor greater than the maximum of 2.0 or 1.5 times the full sample nonresponse adjustment factor were collapsed with suitable adjacent cells.

Initial weighting cells were generally collapsed in reverse order of the cell structure; that is, starting at the bottom of the nesting structure and working up toward the top level of the nesting structure. Race/ethnicity cells within students with disabilities (SD) and English learners (EL) groups, school nonresponse cell, age for grade-based assessments or grade for long-term trend (LTT) age-based assessments, and gender classes were collapsed first. If further collapsing was required after collapsing all race/ethnicity classes, cells were next combined across gender, then age for grade-based or grade for age-based assessments, and finally school nonresponse cells. Cells are never collapsed across SD and EL groups for any sample.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/development_of_final_student_nonresponse_cells_for_the_2022_assessment.aspx

NAEP Technical Documentation Development of Initial Student Nonresponse Cells

Initial student nonresponse cells are generally created within each sample as defined by grade (or age), school type (public or private), and assessment subject (civics, mathematics, reading, or U.S. history). However, when subjects are administered together by way of spiraling, the initial student nonresponse cells are created across the subjects in the same spiral. The rationale behind this decision is that spiraled subjects are in the same schools and the likelihood that an eligible student participates in an assessment is more related to its school than the assessment subject. Nonresponse adjustment procedures are not applied to excluded students or full-time remote students because they are not required to complete an assessment. Full-time remote students are enrolled in brick-and-mortar schools but do not attend school in person.

The initial student nonresponse cells for the various NAEP 2022 samples are described below.

State Public School Samples for Mathematics and Reading Assessments at Grades 4 and 8

The initial student nonresponse cells for these samples were defined within grade, jurisdiction, and Trial Urban District Assessment (TUDA) district hierarchically as follows: Students with disabilities (SD)/English learners (EL) by subject;

school nonresponse cell;

age (classified into "older"¹student and "modal age or younger" student); gender; and

race/ethnicity.

The highest level variable in the cell structure separates students who were classified either as SD or EL from those who are neither, since SD and EL students tend to score lower on assessment tests than non-SD/non-EL students. In addition, the students in the SD or EL groups are further broken down by subject, since rules for excluding students from the assessment generally differ by subject. Non-SD and non-EL students are not broken down by subject, since the exclusion rules do not apply to them.

National Public School Samples for Civics and U.S. History Assessments at Grade 8

The initial student nonresponse cells for these samples were defined using the following nesting structure: SD/EL by subject;

school nonresponse cell;

age (classified into "older" student and "modal age or younger" student); gender; and

race/ethnicity.

National Public School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

The initial student nonresponse cells for these samples were defined using the following nesting structure: SD/EL by subject;

school nonresponse cell;

categorized grade (classified into "lower" and "upper" grade); gender; and

race/ethnicity.

National Private School Samples for Mathematics and Reading Assessments at Grades 4 and 8

The initial weighting cells for these private school samples were formed using the following nesting structure within grade: SD/EL;

school nonresponse cell;

age (classified into "older" student and "modal age or younger" student); gender; and

race/ethnicity.

Although exclusion rules differ by subject, there were not enough SD or EL private school students to break out by subject as was done for the public schools.

National Private School Samples for Civics and U.S. History Assessments at Grade 8

The initial weighting cells for these private school samples were formed using the following nesting structure: SD/EL;

school nonresponse cell;

age (classified into "older" student and "modal age or younger" student); gender; and

race/ethnicity.

National Private School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

The initial weighting cells for these private school samples were formed using the following nesting structure:

Shape257 school nonresponse cell;

Shape258 Shape259 categorized grade (classified into "lower" and "upper" grade); gender; and

Shape260 race/ethnicity.

1 ¹Older students are those born before October 1, 2011 for grade 4 and before October 1, 2007, for grade 8.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/development_of_initial_student_nonresponse_cells_for_the_2022_assessment.aspx

NAEP Technical Documentation Student Nonresponse Adjustment Factor Calculation

In each final student nonresponse adjustment cell $c$ for a given sample, the student nonresponse adjustment factor $STU\_NRAF_{c}$ was computed as

\begin{equation} STU\_NRAF_{c} = \dfrac { \sum_{ k \in S_{c}} \dfrac { STU\_BWT_{k} \times SCH\_TRIM_{k} \times SCH\_NRAF_{k} } {SUBJFAC_{k}} } { \sum_{ k \in R_{c}} \dfrac { STU\_BWT_{k} \times SCH\_TRIM_{k} \times SCH\_NRAF_{k} } {SUBJFAC_{k}} }, \end{equation}

where

$S_{c}$ is the set of all eligible sampled students in cell $s$ for a given sample; $R_{c}$ is the set of all assessed students within $S_{c}$;

$STU\_BWT_{k}$ is the student base weight for a given student $k$;

$SCH\_TRIM_{k}$ is the school-level weight trimming factor for the school associated with student $k$;

$SCH\_NRAF_{k}$ is the school-level nonresponse adjustment factor for the school associated with student $k$; and $SUBJFAC_{k}$ is the subject factor for student $k$.

The student weight used in the calculation above is the adjusted student base weight, without regard to subject, adjusted for school weight trimming and school nonresponse.

Nonresponse adjustment procedures are not applied to excluded students or full-time remote students because these students are not required to complete an assessment. In effect, these students were placed in a separate nonresponse cell by themselves, and all received an adjustment factor of 1. While these students are not included in the analysis of the NAEP scores, weights are provided for them in order to estimate the sizes of these groups and their population characteristics.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/student_nonresponse_adjustment_factor_calculation_for_the_2022_assessment.aspx

Shape263

NAEP Technical Documentation School and Student Weight Trimming Adjustments

Weight trimming is an adjustment procedure that involves detecting and reducing extremely large weights. "Extremely large weights"

generally refer to large sampling weights that were not anticipated in the design of the sample. Unusually large weights are likely to produce large sampling variances for statistics of interest, especially when the large weights are associated with sample cases reflective of rare or atypical characteristics. To reduce the impact of these large weights on variances, weight reduction methods are typically employed. The goal of employing weight reduction methods is to reduce the mean square error of survey estimates. While the trimming of large weights reduces variances, it also introduces some bias. However, it is presumed that the reduction in the variances more than compensates for the increase in the bias, thereby reducing the mean square error and thus improving the accuracy of survey estimates (Potter, 1988). NAEP employs weight trimming at both

the school and student levels.

Trimming of School Base Weights

Trimming of Student Weights

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/school_and_student_weight_trimming_adjustments_for_the_2022_assessment.aspx

Shape264

NAEP Technical Documentation Trimming of School Base Weights

Unusually large school weights can occur under three circumstances:

New Schools: When a school selected from the NAEP new-school sampling frame has an enrollment that is disproportionately large relative to the enrollment of its corresponding school district or Catholic diocese. In other words, when a large new school is selected from a small school district or Catholic diocese.
Private Schools: When a school from the private school frame participates in NAEP but did not participate in the Private School Universe Survey (PSS), the source of the NAEP private school frame. Schools that fall into this category are referred to as PSS nonrespondents and have small probabilities of selection.
Schools with Large Enrollment Increases: When the actual grade enrollment of a school, determined at the time of student sampling, is grossly larger than its enrollment used for school sampling.

If a school's base weight was determined to be too large, the school weight was trimmed. Recall schools were sampled for NAEP with probability proportional to size where size was based on student grade enrollment. If a sampled school had a small grade enrollment, its school base weight was large. To determine if a school's base weight was too large, a comparison was made between a school's base weight and its ideal weight (described below). If a school's base weight was more than three times its ideal weight, the school's base weight was scaled back or trimmed to three times the ideal weight. The trimming was accomplished by way of a trimming factor. The trimming factor for school \ (s\) was calculated using the formula

\begin{equation} SCH\_TRIM_{s} = \left\{\begin{array}{llll} \dfrac{3 \times EXP\_WT_{s}} {SCH\_BWT_{s}} & \text{if } \dfrac{ SCH\_BWT_{s}} { EXP\_WT_{s}}

>3 \\ 1 & \text{otherwise } \\ \end{array}\right. , \end{equation} where

$EXP\_WT_{s}$ is the ideal base weight for school $s$; and

$SCH\_BWT_{s}$ is the actual school base weight for school $s$.

The ideal weight for a school depends on the type of circumstance: whether it was a new school, private school, or school with large grade enrollment increase. Details of the trimming procedure by type of circumstance are described below.

New Schools

New schools with a disproportionately large student enrollment in a particular grade from a school district (or Catholic diocese) that was selected with a small probability of selection were likely candidates to have their school weights trimmed. The school base weights for such schools may be large relative to what they would have been if they had been selected from the NAEP public or private school sampling frame. The ideal weight for a new school was as follows:

$EXP\_WT_{s}$ is the ideal base weight the school would have received if it had been on the NAEP public or private school sampling frame.

For the 2022 NAEP assessment, two grade 8 schools out of 73 participating schools selected from the new-school sampling frame had their weights trimmed.

Private Schools

Private school PSS nonrespondents who participated in NAEP and were found subsequently to have either larger enrollments than assumed at the time of school sampling or an atypical probability of selection given their affiliation, the latter being unknown at the time of sampling, were also likely candidates to have their school weights trimmed. The ideal weight for a PSS nonresponding private school was as follows:

$EXP\_WT_{s}$ is the ideal base weight the school would have received if it had been on the NAEP private school sampling frame with accurate enrollment and known affiliation.

For the 2022 NAEP assessment, there were three private school PSS nonrespondents that participated in NAEP, and none had their weights trimmed.

Schools with Large Enrollment Increases

Schools, other than the PSS nonrespondents described above, whose enrollments determined at the time of student sampling were much larger than those assumed at the time of school sampling were also candidates to have their school weights trimmed. These schools have large relative school weights because their school probabilities of selection were artificially low. The ideal weight for a school with a large grade enrollment increase was as follows:

$EXP\_WT_{s}$ is the ideal base weight the school would have received if it had been on the relevant NAEP public or private school sampling frame with the updated enrollment figure from student sampling.

For the 2022 NAEP assessment, one school at grade 8 with a large grade enrollment increase had its weight trimmed.

Note that for the long-term trend (LTT) assessments, age-specific enrollment was used in the trimming procedure instead of grade enrollment. No LTT schools had their weights trimmed.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/trimming_of_school_base_weights_for_the_2022_assessment.aspx

Shape265

NAEP Technical Documentation Trimming of Student Weights

Large student weights generally come from compounding nonresponse adjustments at the school and student levels with artificially low school selection probabilities, which can result from inaccurate enrollment data on the school frame used to define the school size measure. Even though measures are in place to limit the number and size of excessively large weights—such as the implementation of adjustment factor size constraints in both the school and student nonresponse procedures and the use of the school trimming procedure—large student weights can occur due to compounding effects of the various weighting components.

The student weight trimming procedure uses a multiple median rule to detect excessively large student weights. Any student weight within a given trimming group greater than a specified multiple of the median weight value of the given trimming group has its weight scaled back to that threshold. Student weight trimming was implemented separately by grade (or age, in the case of long-term trend [LTT]), school type (public or private), and subject. Initially, the threshold was set to 3.5. If too many student weights were being trimmed for a particular sample, the threshold was increased to reduce the number of records trimmed. The multiples and the trimming groups are defined for each sample below. Note that because in the initial runs of the national private school samples for mathematics and reading at grades 4 and 8 too many records were getting their weights trimmed, the threshold in those samples was increased to 4.5.

State Public School Samples for Mathematics and Reading at Grades 4 and 8

For these samples, the initial multiple used was 3.5, and the trimming groups were formed within each jurisdiction by Trial Urban District Assessment (TUDA) district vs. the balance of the state for states with TUDA districts.

National Private School Samples for Mathematics and Reading at Grades 4 and 8

For these samples, the initial multiple used was 4.5, and the trimming groups were formed by affiliation (Catholic, Non-Catholic).

National Public School Samples for Civics and U.S. History at Grade 8

For these samples, the initial multiple used was 3.5, and the trimming groups were formed by dichotomies of low/high percentage of American Indian/Alaska Native students (5 percent and below, above 5 percent) and Black and Hispanic students (15 percent and below, above 15 percent).

National Private School Samples for Civics and U.S. History at Grade 8

For these samples, the initial multiple used was 3.5, and the trimming groups were formed by affiliation (Catholic, Non-Catholic).

National Public School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

For these samples, the initial multiple used was 3.5, and the trimming groups were defined by region and school oversampling factor for public schools. The school oversampling factor separated, into different trimming groups, schools that had different probabilities of selection by design due to the desire to increase the numbers of Black, Hispanic, and American Indian/Alaska Native students in the sample.

National Private School Samples for Mathematics and Reading LTT Assessments at Ages 9 and 13

For these samples, the initial multiple used was 3.5, and the trimming groups were formed by affiliation (Catholic, Non-Catholic).

The procedure computes the median of the nonresponse-adjusted student weights in the trimming group $g$ for a given grade (or age) and subject sample. Any student $k$ with a weight more than $M$ times the median received a trimming factor calculated as

\begin{equation} STU\_TRIM_{gk} = \left\{\begin{array}{llll} \dfrac{M \times MEDIAN_{g}} {STUWGT_{gk}} & \text{if } STUWGT_{gk} < M \times MEDIAN_{g} \\ 1 & \text{otherwise } \\ \end{array}\right. , \end{equation}

where

$M$ is the trimming multiple,

$MEDIAN_{g}$ is the median of nonresponse-adjusted student weights in trimming group $g$, and

$STUWGT_{gk}$ is the weight after student nonresponse adjustment for student in trimming group $g$.

In the 2022 assessment, very few students had weights considered excessively large. Out of the approximately 483,700 students included in the combined grade- based 2022 assessment samples, 35 students had their weights trimmed. None of the approximately 33,500 LTT students had their weights trimmed.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/trimming_of_student_weights_for_the_2022_assessment.aspx

Shape266

NAEP Technical Documentation Student Weight Raking Adjustment

Weighted estimates of population totals for student-level subgroups for a given grade will vary across subjects even though the student samples for each subject generally come from the same schools. These differences are the result of sampling error associated with the random assignment of subjects to students through a process known as spiraling. For state assessments in particular, any difference in demographic estimates between subjects, no matter how small, may raise concerns about data quality. To remove these random differences and potential data quality concerns, a step was added to the NAEP weighting procedure in 2009. This step adjusts the student weights in such a way that the weighted sums of

Development of Final Raking Dimensions Raking Adjustment Control Totals

Raking Adjustment Factor Calculation

population totals for specific student groups are the same across all subjects. It was implemented using a raking procedure and applied only to public school assessments.

Raking is a weighting procedure based on the iterative proportional fitting process developed by Deming and Stephan (1940) and involves simultaneous ratio adjustments to two or more marginal distributions of population totals. Each set of marginal population totals is known as a dimension, and each population total in a dimension is referred to as a control total. Raking is carried out in a sequence of adjustments. Sampling weights are adjusted to one marginal distribution and then to the second marginal distribution, and so on. One cycle of sequential adjustments to the marginal distributions is called an iteration. The procedure is repeated until convergence is achieved. The criterion for convergence can be specified either as the maximum number of iterations or an absolute difference (or relative absolute difference) from the marginal population totals. More discussion on raking can be found in Oh and Scheuren (1987).

For NAEP 2022, the student raking adjustment was carried out for each public student sample. Similar to previous years, raking was not performed for any of the private school student samples or for student samples in the long-term trend (LTT) assessments at age 9. The dimensions used in the raking process for each public school student sample were race/ethnicity, gender, and student disability (SD) and English learner (EL) status. (Since 2013, National School Lunch Program [NSLP] eligibility has not been used as a raking dimension because of the instability of these data in many states.)

For the public school student samples in mathematics and reading at grades 4 and 8, the student raking adjustment was carried out separately in each state and TUDA district. The control totals for the raking dimensions for these student samples were obtained from the NAEP student sample weights of the mathematics and reading public samples combined.

For the public school student samples in civics and U.S. history at grade 8, the student raking adjustment was carried out at the national level. The control totals for the raking dimensions for these samples were obtained by summing the NAEP grade 8 student sample weights of the mathematics and reading public samples combined.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/student_weight_raking_adjustment_for_the_2022_assessment.aspx

Shape267

NAEP Technical Documentation Development of Final Raking Dimensions

The raking procedure involved three dimensions. The variables used to define the dimensions are listed below along with the categories making up the initial raking cells for each dimension.

Race/Ethnicity

White, not Hispanic
Black, not Hispanic
Hispanic
Asian
American Indian/Alaska Native
Native Hawaiian/Pacific Islander
Two or More Races

Student disability (SD)/English learner (EL) status

SD, but not EL
EL, but not SD
SD and EL
Neither SD nor EL

Gender

Male
Female

For the reading and mathematics samples, in states containing districts that participated in Trial Urban District Assessments (TUDA) at grades 4 and 8, the initial cells were created separately for each TUDA district and the balance of the state. For the civics and U.S. history samples at grade 8, the initial cells were created at the national level. Similar to the procedure used for school and student nonresponse adjustments, limits were placed on the magnitude of the cell sizes and adjustment factors to prevent unstable raking adjustments that could have resulted in unacceptably large or small adjustment factors. Levels of a dimension were combined whenever 1) there were fewer than 30 assessed, excluded, or full-time remote students (20 for any of the replicates) in a category, 2) the smallest adjustment was less than 0.5, or 3) the largest adjustment was greater than 2 for the full sample or for any replicate.

If collapsing was necessary for the race/ethnicity dimension, individual groups with similar student achievement levels were combined first. If further collapsing was necessary, the next closest race/ethnicity group was combined as well, and so on until all collapsing rules were satisfied. In some instances, all seven categories had to be collapsed.

If collapsing was necessary for the SD/EL dimension, the SD/not EL and SD/EL categories were combined first, followed by EL/not SD if further collapsing was necessary. In some instances, all four categories had to be collapsed.

Collapsing gender is generally not expected. However, in the rare event that it is necessary, male and female categories would be collapsed.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/development_of_final_raking_dimensions_for_the_2022_assessment.aspx

Shape268

NAEP Technical Documentation Raking Adjustment Control Totals

The control totals used in the raking procedure for NAEP 2022 at grades 4 and 8 were estimates of the student population derived from the set of assessed, excluded, and full- time remote students pooled across subjects (mathematics and reading). The control totals for category $c$ within dimension $d$ were computed as

\begin{equation} TOTAL_{c(d)} = \sum_{ R_{c(d)} \smile E_{c(d)}} \dfrac { STU\_BWT_{k} \times SCH\_TRIM_{k} \times SCH\_NRAF_{k} \times STU\_NRAF_{k} }

{SUBJFAC_{k}}, \end{equation} where

$R_{c(d)}$ is the set of all assessed students in category $c$ of dimension $d$;

$E_{c(d)}$ is the set of all excluded or full-time remote students in category $c$ of dimension $d$; $STU\_BWT_{k}$ is the student base weight for a given student $k$;

$SCH\_TRIM_{k}$ is the school-level weight trimming factor for the school associated with student $k$;

$SCH\_NRAF_{k}$ is the school-level nonresponse adjustment factor for the school associated with student $k$; $STU\_NRAF_{k}$ is the student-level nonresponse adjustment factor for student $k$; and

$SUBJFAC_{k}$ is the subject factor for student $k$.

The student weight used in the calculation of the control totals above is the student base weight, without regard to subject, adjusted for school weight trimming, school nonresponse, and student nonresponse. Control totals were computed for the full sample and for each replicate independently.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/raking_adjustment_control_totals_for_the_2022_assessment.aspx

Shape269

NAEP Technical Documentation Raking Adjustment Factor Calculation

For assessed, excluded, and full-time remote students in a given subject, the raking adjustment factor $STU\_RAKE_{k}$ was computed as below. First, the weight for student $k$ was initialized as

\begin{equation} STUSAWT_{k}^{adj(0)} = STU\_BWT_{k} \times SCH\_TRIM_{k} \times SCH\_NRAF_{k} \times STU\_NRAF_{k} \times SUBJFAC_{k} ,

\end{equation} where

$STU\_BWT_{k}$ is the student base weight for a given student $k$;

$SCH\_TRIM_{k}$ is the school-level weight trimming factor for the school associated with student $k$;

$SUBJFAC_{k}$ is the subject factor for student $k$.

Then, the sequence of weights for the first iteration was calculated as follows for student $k$ in category $c$ of dimension $d$:

for dimension 1: \begin{equation} STUSAWT_{k}^{adj(1)} = \dfrac {TOTAL_{c(1)}} { \sum_{ R_{c(1)} \smile E_{c(1)}} {STUSAWT_{k}^{adj(0)} } } \times STUSAWT_{k}^{adj(0)} , \end{equation}

for dimension 2: \begin{equation} STUSAWT_{k}^{adj(2)} = \dfrac {TOTAL_{c(2)}} { \sum_{ R_{c(2)} \smile E_{c(2)}} {STUSAWT_{k}^{adj(1)} } } \times STUSAWT_{k}^{adj(1)} , \end{equation}

for dimension 3: \begin{equation} STUSAWT_{k}^{adj(3)} = \dfrac {TOTAL_{c(3)}} { \sum_{ R_{c(3)} \smile E_{c(3)}} {STUSAWT_{k}^{adj(2)} } } \times STUSAWT_{k}^{adj(2)} , \end{equation}

where

$R_{c(d)}$ is the set of all assessed students in category $c$ of dimension $d$;

$E_{c(d)}$ is the set of all excluded or full-time remote students in category $c$ of dimension $d$; and $TOTAL_{c(d)}$ is the control total for category $c$ of dimension $d$.

The process is said to converge if the maximum difference between the sum of adjusted weights and the control totals is 1.0 for each category in each dimension. If after the sequence of adjustments the maximum difference was greater than 1.0, the process continues to the next iteration, cycling back to the first dimension with the initial weight for student $k$ equaling $STUSAWT_{k}^{adj(3)}$ from the previous iteration. The process continued until convergence was reached.

Once the process converged, the adjustment factor was computed as

\begin{equation} STU\_RAKE_{k} = \dfrac {STUSAWT_{k}} { STU\_BWT_{k} \times SCH\_TRIM_{k} \times SCH\_NRAF_{k} \times STU\_NRAF_{k} \times SUBJFAC_{k} } , \end{equation}

where

Shape270 $STUSAWT_{k}$ is the weight for student $k$ after convergence.

The process was done independently for the full sample and for each replicate.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/raking_adjustment_factor_calculation_for_the_2022_assessment.aspx

Shape271

NAEP Technical Documentation Computation of Replicate School Weights

In addition to the full-sample weight, a set of 62 replicate weights was provided for each school. These replicate weights are used in calculating the sampling variance of estimates obtained from the data, using the jackknife repeated replication method. The method of deriving these weights was aimed at reflecting the features of the sample design appropriately for each sample, so that when the jackknife variance estimation procedure is implemented, approximately unbiased estimates of sampling variance are obtained. This section gives the specifics for generating the replicate weights for the 2022 assessment samples.

The theory that underlies the jackknife variance estimators used in NAEP studies is discussed in the section Replicate Variance Estimation.

For each sample, replicates were formed in two steps. First, each school was assigned to one or more of 62 replicate strata. This step differed for the age-based long-term trend (LTT) samples and the grade-based samples as described in the separate "Defining Variance Strata and Forming Replicates" links above. In the next step, a random subset of schools in each replicate

stratum was excluded. The remaining subset and all schools in the other replicate strata then constituted one of the 62 replicates.

Defining Variance Strata and Forming Replicates (age-based samples)

Defining Variance Strata and Forming Replicates (grade-based samples)

Replicate Variance Estimation

For the 2022 LTT assessments, the same PSUs were sampled in 2022 and 2020. In fact, any comparison of the 2022 and 2020 estimates is a comparison of the same schools, so each school must be in the same variance stratum and variance unit in the two years so that the jackknife variance estimation will correctly reflect this dependence. To ensure that standard errors for trend would be calculated appropriately, each noncertainty PSU was assigned the same variance stratum and variance unit as in 2020. Likewise,

in certainty PSUs, schools that were retained in 2022 from the 2020 sample were assigned the same variance stratum and variance unit as in 2020.

A replicate weight was calculated for each of the 62 replicates using weighting procedures similar to those used for the full-sample weight. Each replicate base weight contains an additional component, known as a replicate factor, to account for the subsetting of the sample to form the replicate. By repeating the various weighting procedures on each set of replicate base weights, the impact of these procedures on the sampling variance of an estimate is appropriately reflected in the variance estimate.

Each of the 62 replicate weights for school s in stratum j can be expressed as follows:

\begin{equation} \begin{aligned} SCH\_WGT_{js}(r)= {} & SCH\_BWT_{js}(r) \times SCH\_NRAF_{js}(r) \times\\ &SCH\_TRIM_{js} \times SCHSESWT_{js} \times SCH\_SUBJ\_AF_{js} \end{aligned} \end{equation}

where

Shape272 $SCH\_BWT_{js}(r)$ is the replicate school base weight for replicate $r$;

Shape273 $SCH\_NRAF_{js}(r)$ is the school-level nonresponse adjustment factor for replicate $r$;

Shape274 $SCH\_TRIM_{js}$ is the school-level weight trimming adjustment factor;

Shape275 $SCHSESWT_{js}$ is the school-level session assignment weight; and

$SCH\_SUBJ\_AF_{js}$ is the small-school subject adjustment factor.

Specific school nonresponse adjustment factors were calculated separately for each replicate, as indicated by the index (r) in the formula, and applied to the replicate school base weights. Computing separate nonresponse adjustment factors for each replicate allows resulting variances from the use of the final school replicate weights to reflect components of variance due to this weight adjustment.

School weight trimming adjustments were not replicated, that is, not calculated separately for each replicate. Instead, each replicate used the school trimming adjustment factors derived for the full sample. Statistical theory for replicating trimming adjustments under the jackknife approach has not been developed in the literature. Due to the absence of a statistical framework, and since relatively few school weights in NAEP require trimming, the weight trimming adjustments were not replicated.

In addition, the school-level session assignment weight and the small-school subject adjustment factor also used the same factors derived for the full sample.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computation_of_replicate_school_weights_for_variance_estimation_for_the_2022_assessment.aspx

Shape276

NAEP Technical Documentation Computation of Replicate Student Weights for Variance Estimation

In addition to the full-sample weight, a set of 62 replicate weights was provided for each student. These replicate weights are used in calculating the sampling variance of estimates obtained from the data, using the jackknife repeated replication method. The method of deriving these weights was aimed at reflecting the features of the sample design appropriately for each sample, so that when the jackknife variance estimation procedure is implemented, approximately unbiased estimates of sampling variance are obtained. This section gives the specifics for generating the replicate weights for the 2022 assessment samples.

The theory that underlies the jackknife variance estimators used in NAEP studies is discussed in the section Replicate Variance Estimation.

In general, the process of creating jackknife replicate weights takes place at both the school and student level. The precise implementation differs between those samples that involve the selection of Primary Sampling Units (PSUs) and those where the school is the first stage of sampling. The procedure for this second kind of sample also differed starting in 2011 from all

Defining Variance Strata and Forming Replicates

Computing School-Level Replicate Factors

Computing Student-Level Replicate Factors

Replicate Variance Estimation

previous NAEP assessments. The change that was implemented permitted the introduction of a finite population correction factor at the school sampling stage, developed by Rizzo and Rust (2011). In assessments prior to 2011, this adjustment factor has always been implicitly assumed equal to 1.0, resulting in some overestimation of the sampling variance.

PSU-Based (i.e., Age-Based) Samples

For the 2022 long-term trend (LTT) samples, which involve the selection of PSUs, the process for computing replicate student weights for variance estimation is very similar to the one that was used in 2020. The same PSUs were sampled in 2022 and 2020. In fact, any comparison of the 2022 and 2020 estimates is a comparison of the same schools, so each school must be in the same variance stratum and variance unit in the two years so that the jackknife variance estimation will correctly reflect this dependence. To ensure that standard errors for trend would be calculated appropriately, each noncertainty PSU was assigned the same variance stratum and variance unit as in 2020. Likewise, in certainty PSUs, schools that were retained in 2022 from the 2020 sample were assigned the same variance stratum and variance unit as in 2020. For more information about computing replicate student weights for the LTT samples see here.

Grade-Based Samples

The process for computing replicate student weights for variance estimation for the 2022 grade-based samples is as follows:

For each sample, the calculation of replicate weighting factors at the school level was conducted in a series of steps. First, each school was assigned to one of 62 variance estimation strata. Then, a random subset of schools in each variance estimation stratum was assigned a replicate factor of between 0 and 1. Next, the remaining subset of schools in the same variance stratum was assigned a complementary replicate factor greater than 1. All schools in the other variance estimation strata were assigned a replicate factor of exactly 1. This process was repeated for each of the 62 variance estimation strata so that 62 distinct replicate factors were assigned to each school in the sample.

This process was then repeated at the student level. Here, each individual sampled student was assigned to one of 62 variance estimation strata, and 62 replicate factors with values either between 0 and 1, greater than 1, or exactly equal to 1 were assigned to each student.

For example, consider a single hypothetical student. For replicate 37, that student’s student replicate factor might be 0.8, while for the school to which the student belongs, for replicate 37, the school replicate factor might be 1.6. Of course, for a given student, for most replicates, either the student replicate factor, the school replicate factor, or (usually) both, is equal to 1.0.

A replicate weight was calculated for each student, for each of the 62 replicates, using weighting procedures similar to those used for the full-sample weight. Each replicate weight contains the school and student replicate factors described above. By repeating the various weighting procedures on each set of replicates, the impact of these procedures on the sampling variance of an estimate is appropriately reflected in the variance estimate.

Each of the 62 replicate weights for student $k$ in school $s$ in stratum $j$ can be expressed as

\begin{equation} \begin{aligned} FSTUWGT_{jsk}(r) = {} & STU\_BWT_{jks} \times SCH\_REPFAC_{js}(r) \times SCH\_NRAF_{js}(r) \times \\ & STU\_REPFAC_{jsk}(r) \times STU\_NRAF_{jsk}(r) \times \\ & SCH\_TRIM_{js} \times STU\_TRIM_{jsk} \times STU\_RAKE_{jsk}(r) \end{aligned}, \end{equation} where

Shape277 $STU\_BWT_{jks}$ is the student base weight;

Shape278 $SCH\_REPFAC_{js}(r)$ is the school-level replicate factor for replicate $r$;

Shape279 $SCH\_NRAF_{js}(r)$ is the school-level nonresponse adjustment factor for replicate $r$;

Shape280 $STU\_REPFAC_{jsk}(r)$ is the student-level replicate factor for replicate $r$;

Shape281 $STU\_NRAF_{jsk}(r)$ is the student-level nonresponse adjustment factor for replicate $r$;

Shape282 $SCH\_TRIM_{js}$ is the school-level weight trimming adjustment factor;

Shape283 $STU\_TRIM_{jsk}$ is the student-level weight trimming adjustment factor; and

Shape284 $STU\_RAKE_{jsk}(r)$ is the student-level raking adjustment factor for replicate $r$.

Specific school and student nonresponse and student-level raking adjustment factors were calculated separately for each replicate, as indicated by the index $r$ in the formula, and applied to the replicate student base weights. Computing separate nonresponse and raking adjustment factors for each replicate allows resulting variances from the use of the final student replicate weights to reflect components of variance due to these various weight adjustments.

School and student weight trimming adjustments were not replicated, that is, not calculated separately for each replicate. Instead, each replicate used the school and student trimming adjustment factors derived for the full sample. Statistical theory for replicating trimming adjustments under the jackknife approach has not been developed in the literature. Due to the absence of a statistical framework, and since relatively few school and student weights in NAEP require trimming, the weight trimming adjustments were not replicated.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computation_of_replicate_student_weights_for_variance_estimation_for_the_2022_assessment.aspx

Shape285

NAEP Technical Documentation Computing School-Level Replicate Factors

The school-level replication procedures differed for the age-based samples and the grade-based samples because the latter incorporate finite population corrections.

Age-Based Samples

For the NAEP 2022 age-based long-term trend (LTT) assessments, the school-level replication was carried out using the same procedures used for 2020 LTT. Those procedures are described here.

Grade-Based Samples

The replicate variance estimation approach for the grade-based civics, mathematics, reading, and U.S. history assessments involved finite population corrections at the school level. The calculation of school-level replicate factors for these assessments depended upon whether or not a school was selected with certainty. For certainty schools, the school-level replicate factors for all replicates are set to unity–this is true regardless of whether or not the variance replication method uses finite population corrections–since certainty schools are not subject to sampling variability. Alternatively, one can view the finite population correction factor for such schools as being equal to zero. Thus, for each certainty school in a given assessment, the school-level replicate factor for each of the 62 replicates ($r=1, ..., 62$) was assigned as

\begin{equation} SCH\_REPFAC_{js}(r)=1 , \displaystyle \end{equation}

where $SCH\_REPFAC_{js}(r)$ is the school-level replicate factor for school $s$ in primary stratum $j$ for the $r$-th replicate.

For noncertainty schools, where preliminary variance strata were formed by grouping schools into pairs or triplets, school-level replicate factors were calculated for each of the 62 replicates based on this grouping. For schools in variance strata comprising pairs of schools, the school-level replicate factors, $SCH\_REPFAC_{js}(r) = 1,..., 62$, were calculated as

\begin{equation} SCH\_REPFAC_{js}(r) = \left\{\begin{array}{llll} 1 + \sqrt{(1-min(\pi_{j1}, \pi_{j2}))}, & \text{for } js \in R_{jr}, U_{js} = 1 \\ 1 - \sqrt{(1-min(\pi_{j1},

\pi_{j2}))}, & \text{for } js \in R_{jr}, U_{js} = 2 \\ 1, & \text{for } js \notin R_{jr} \end{array}\right. , \end{equation}

where

Shape286
Shape287
Shape288

$min(\pi_{j1}, \pi_{j2})$ is the smallest school probability between the two schools comprising $R_{jr}$;

$R_{jr}$ is the set of schools within the $r$-th variance stratum for primary stratum $j$; and

$U_{js}$ is the variance unit (1 or 2) for school $s$ in primary stratum $j$.

For triples (i.e., variance strata comprising 3 schools), the replicate factors are perturbed to something other than 1.0 for two different variance strata, rather than just for one stratum as in the case of pairs (i.e., variance strata comprising 2 schools). The replicate factors are perturbed in variance stratum $r$ and variance stratum $r'$, where $r'$ is furthest away from variance stratum $r$ in either direction (i.e., before or after stratum $r$). Because there are 62 replicates, the stratum furthest away from stratum $r$ would be the stratum whose number is the number of stratum $r$ plus or minus half of 62, depending on whether $r$ is greater or less than 31. In other words, $r'=r+31$ \ (mod\) $62$. For example, if variance stratum 40 has three schools, replicate factors are perturbed in variance stratum 40 ($r$) and variance stratum 9 ($r'$). The school-level replicate factors $SCH\_REPFAC_{js}(r)$, $r = 1,..., 62$, were calculated as follows:

For school $s$ from primary stratum $j$ variance stratum $r$,

\begin{equation} SCH\_REPFAC_{js}(r) = \left\{\begin{array}{llll} 1 + \dfrac {\sqrt{(1-min(\pi_{j1}, \pi_{j2}, \pi_{j3}))}} {2}, & \text{for } js \in R_{jr}, U_{js} = 1 \\ 1 +

\dfrac {\sqrt{(1-min(\pi_{j1}, \pi_{j2}, \pi_{j3}))}} {2}, & \text{for } js \in R_{jr}, U_{js} = 2 \\ 1 - \sqrt{(1-min(\pi_{j1}, \pi_{j2}, \pi_{j3}))}, & \text{for } js \in R_{jr}, U_{js} = 3 \end{array}\right. , \end{equation}

while for variance stratum $r'$,

\begin{equation} SCH\_REPFAC_{js}(r’) = \left\{\begin{array}{llll} 1 + \dfrac {\sqrt{(1-min(\pi_{j1}, \pi_{j2}, \pi_{j3}))}} {2}, & \text{for } js \in R_{jr}, U_{js} = 1 \\ 1 -

\sqrt{(1-min(\pi_{j1}, \pi_{j2}, \pi_{j3}))}, & \text{for } js \in R_{jr}, U_{js} = 2 \\ 1 + \dfrac {\sqrt{(1-min(\pi_{j1}, \pi_{j2}, \pi_{j3}))}} {2}, & \text{for } js \in R_{jr}, U_{js} = 3 \\ \end{array}\right. , \end{equation}

and for all other variance strata, further called $r$ with an asterisk ($r^*$) (that is, strata other than variance strata $r$ and $r'$),

\begin{equation} SCH\_REPFAC_{js}(r^*) = 1 , \end{equation} where

$min(\pi_{j1}, \pi_{j2}, \pi_{j3})$ is the smallest school probability among the three schools comprising $R_{jr}$; $R_{jr}$ is the set of schools within the $r$-th variance stratum for primary stratum $r$; and

$U_{js}$ is the variance unit (1, 2, or 3) for school $s$ in primary stratum $j$.

In primary strata with fewer than 62 variance strata, the replicate weights for the “unused” variance strata (the remaining ones up to 62) for these schools were set equal to the school base weight (so that those replicates contribute nothing to the variance estimate).

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computing_school_level_replicate_factors_for_the_2022_assessment.aspx

NAEP Technical Documentation Computing Student-Level Replicate Factors

The student-level replication procedures differed for the age-based samples and the grade-based samples because the latter incorporate finite population corrections.

Age-Based Samples

For the NAEP 2022 age-based long-term trend (LTT) assessments, the student-level replication was carried out using the same procedures used for 2020 LTT. Those procedures are described here.

Grade-Based Samples

For the grade-based civics, mathematics, reading, and U.S. history assessment samples, which involved school-level finite population corrections, the student-level replication factors were calculated the same way regardless of whether or not the student was in a certainty school.

For students in student-level variance strata comprising pairs of students, the student-level replicate factors, $STU\_REPFAC_{jsk}(r)$, $r = 1,..., 62$, were calculated as

\begin{equation} STU\_REPFAC_{jsk}(r) = \left\{\begin{array}{llll} 1 + \sqrt {\pi_{s}}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 1 \\ 1 - \sqrt {\pi_{s}}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 2 \\ 1, & \text{for } jsk \notin R_{jsr} \end{array}\right. , \end{equation}

where

$\pi_{s}$ is the probability of selection for school $s$;

$R_{jsr}$ is the set of students within the $r$-th variance stratum for school $s$ in primary stratum $j$; and $U_{jsk}$ is the variance unit (1 or 2) for student $k$ in school $s$ in stratum $j$.

For triples (i.e., variance strata comprising three students), the replicate factors are perturbed to something other than 1.0 for two different variance strata, rather than just for one stratum as in the case of pairs (i.e., variance strata comprising 2 students). The replicate factors are perturbed in variance stratum $r$ and variance stratum $r'$, where $r'$ is furthest away from variance stratum $r$ in either direction (i.e., before or after stratum $r$). Because there are 62 replicates, the stratum furthest away from stratum $r$ would be the stratum whose number is the number of stratum $r$ plus or minus half of 62, depending on whether $r$ is greater or less than 31. In other words, $r'=r+31$ \ (mod\) $62$. For example, if variance stratum 1 has three students, replicate factors are perturbed in variance stratum 1 ($r$) and variance stratum 32 ($r'$). The student-level replicate factors $STU\_REPFAC_{jsk}(r)$, $r = 1,..., 62$, were calculated as follows:

\begin{equation} STU\_REPFAC_{jsk}(r) = \left\{\begin{array}{llll} 1 + \dfrac {\sqrt {\pi_{s}}} {2}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 1 \\ 1 + \dfrac {\sqrt {\pi_{s}}}

{2}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 2 \\ 1 - \sqrt {\pi_{s}}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 3 \end{array}\right. , \end{equation} while for variance stratum $r' = r + 31$ $mod$ $62$,

\begin{equation} STU\_REPFAC_{jsk}(r') = \left\{\begin{array}{llll} 1 + \dfrac {\sqrt {\pi_{s}}} {2}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 1 \\ 1 - \sqrt {\pi_{s}}, &

\text{for } jsk \in R_{jsr}, U_{jsk} = 2 \\ 1 + \dfrac {\sqrt {\pi_{s}}} {2}, & \text{for } jsk \in R_{jsr}, U_{jsk} = 3 \end{array}\right. , \end{equation} and for all other variance strata, further called $r$ with an asterisk ($r^*$), (that is, variance strata other than strata $r$ and $r'$),

\begin{equation} STU\_REPFAC_{jsk}(r^*) = 1 , \end{equation} where

Shape290 $\pi_{s}$ is the probability of selection for school $s$;

$R_{jsr}$ is the set of students within the $r$-th replicate stratum for school $s$ in stratum $j$; and $U_{jsk}$ is the variance unit (1, 2, or 3) for student $k$ in school $s$ in stratum $j$.

Note, for students in certainty schools, where $\pi_{s}=1$, the student replicate factors are 2 and 0 in the case of pairs, and 1.5, 1.5, and 0 in the case of triples.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/computing_student_level_replicate_factors_for_the_2022_assessment.aspx

Shape291

NAEP Technical Documentation Defining Variance Strata and Forming Replicates

For NAEP 2022, the procedure used to define variance strata and form replicates differed for the age-based samples and the grade-based samples.

Age-Based Samples

In the NAEP 2022 age-based assessments for long-term trend (LTT), the procedure used to define variance strata and form replicates was the same one used for the 2020 LTT assessments. That procedure is described here .

Grade-Based Samples

In the NAEP 2022 grade-based assessments, replicates were formed separately for each sample indicated by grade (4 or 8), school type (public or private), and assessment subject (civics, mathematics, reading, and U.S. history). To reflect the school-level finite population corrections in the variance estimators for these two-stage samples, replication was carried out at both the school and student levels.

The first step in forming replicates was to create preliminary variance strata in each primary stratum. This was done by sorting the appropriate sampling unit (school or student) in the order of its selection within the primary stratum and then pair off adjacent sampling units into preliminary variance strata. Sorting sample units by their order of sample selection reflects the implicit stratification and systematic sampling features of the sample design. Within each primary stratum with an even number of sampling units, all of the preliminary variance strata consisted of pairs of sampling units. However, within primary strata with an odd number of sampling units, all but one variance strata consisted of pairs of sampling units, while the last one consisted of three sampling units.

The next step is to form the final variance strata by combining preliminary strata if appropriate. If there were more than 62 preliminary variance strata within a primary stratum, the preliminary variance strata were grouped to form 62 final variance strata. This grouping effectively maximized the distance in the sort order between grouped preliminary variance strata. The first 62 preliminary variance strata, for example, were assigned to 62 different final variance strata in order (1 through 62), with the next 62 preliminary variance strata assigned to final variance strata 1 through 62, so that, for example, preliminary variance stratum 1, preliminary variance stratum 63, preliminary variance stratum 125 (if in fact there were that many), etc., were all assigned to the first final variance stratum.

If, on the other hand, there were fewer than 62 preliminary variance strata within a primary stratum, then the number of final variance strata was set equal to the number of preliminary variance strata. For example, consider a primary stratum with 111 sampled units sorted in their order of selection. The first two units were in the first preliminary variance stratum; the next two units were in the second preliminary variance stratum, and so on, resulting in 54 preliminary variance strata with two sample units each (doublets). The last three sample units were in the 55th preliminary variance stratum (triplet). Since there are no more than 62 preliminary variance strata, these were also the final variance strata.

Within each preliminary variance stratum containing a pair of sampling units, one sampling unit was randomly assigned as the first variance unit and the other as the second variance unit. Within each preliminary variance stratum containing three sampling units, the three first-stage units were randomly assigned variance units 1 through 3.

Mathematics and Reading Assessments (Grades 4 and 8)

At the school level for these samples, formation of preliminary variance strata did not pertain to certainty schools, since they are not subject to sampling variability, but only to noncertainty schools. The primary stratum for noncertainty schools was the highest school-level sampling stratum variable listed below, and the order of selection was defined by sort order on the school sampling frame.

Trial Urban District Assessment (TUDA) districts, remainder of states (for states with TUDAs), or entire states for the public school samples at grades 4 and 8; and Private school affiliation (Catholic, non-Catholic) for the private school samples at grades 4 and 8.

At the student level, all students were assigned to variance strata. The primary stratum was school, and the order of selection was defined by session number and position on the administration schedule.

Within each pair of preliminary variance strata, one first-stage unit, designated at random, was assigned as the first variance unit and the other first-stage unit as the second variance unit. Within each triplet preliminary variance stratum, the three schools were randomly assigned variance units 1 through 3.

Civics and U.S. History Assessments (Grade 8)

The nation (50 states and the District of Columbia) for the public school samples at grade 8; and Private school affiliation (Catholic, non-Catholic) for the private school samples at grade 8.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/defining_variance_strata_and_forming_replicates_for_the_2022_assessment.aspx

NAEP Technical Documentation Replicate Variance Estimation

Variances for NAEP assessment estimates are computed using the paired jackknife replicate variance procedure. This technique is applicable for common statistics, such as means and ratios, and differences between these for different subgroups, as well as for more complex statistics such as linear or logistic regression coefficients.

In general, the paired jackknife replicate variance procedure involves initially pairing clusters of first-stage sampling units to form $H$ variance strata $h = 1, 2, 3, ..., H$ with two units per stratum. The first replicate is formed by assigning, to one unit at random from the first variance stratum, a replicate weighting factor of less than 1.0, while

assigning the remaining unit a complementary replicate factor greater than 1.0, and assigning all other units from the other $H - 1$ strata a replicate factor of 1.0. This procedure is carried out for each variance stratum resulting in $H$ replicates, each of which provides an estimate of the population total.

In general, this process is repeated for subsequent levels of sampling. In practice, this is not practicable for a design with three or more stages of sampling, and the marginal improvement in precision of the variance estimates would be negligible in all such cases in the NAEP setting. Thus in NAEP, when a two-stage design is used–sampling schools and then students–beginning in 2011 replication is carried out at both stages for the purpose of computing replicate student weights. The change implemented in 2011 permitted the introduction of a finite population correction factor at the school sampling stage. Prior to 2011, replication was only carried out at the first stage of selection. See Rizzo and Rust (2011) for a description of the methodology.

When a three-stage design is used, involving the selection of geographic Primary Sampling Units (PSUs), then schools, and then students, the replication procedure is only carried out at the first stage of sampling (the PSU stage for noncertainty PSUs, and the school stage within certainty PSUs). In this situation, the school and student variance components are correctly estimated, and the overstatement of the between-PSU variance component is relatively very small.

The jackknife estimate of the variance for any given statistic is given by the following formula:

\begin{equation} \nu(\hat{t}) =\sum_{h=1}^{H} {(\hat{t}_{h}-\hat{t})^2}, \end{equation} where

$\hat{t}$ represents the full sample estimate of the given statistic; and $\hat{t}_{h}$ represents the corresponding estimate for replicate $h$.

Each replicate undergoes the same weighting procedure as the full sample so that the jackknife variance estimator reflects the contributions to or reductions in variance resulting from the various weighting adjustments.

The NAEP jackknife variance estimator is based on 62 variance strata resulting in a set of 62 replicate weights assigned to each school and student.

The basic idea of the paired jackknife variance estimator is to create the replicate weights so that use of the jackknife procedure results in an unbiased variance estimator for totals and means, which is also reasonably efficient (i.e., has a low variance as a variance estimator). The jackknife variance estimator will then produce a consistent (but not fully unbiased) estimate of variance for (sufficiently smooth) nonlinear functions of total and mean estimates such as ratios, regression coefficients, and so forth (Shao and Tu 1995).

The development below shows why the NAEP jackknife variance estimator returns an unbiased variance estimator for totals and means, which is the cornerstone to the asymptotic results for nonlinear estimators. See for example Rust (1985). This paper also discusses why this variance estimator is generally efficient (i.e., more reliable than alternative approaches requiring similar computational resources).

The development is done for an estimate of a mean based on a simplified sample design that closely approximates the sample design for first-stage units used in the NAEP studies. The sample design is a stratified random sample with $H$ strata with population weights $W_{h}$, stratum sample sizes $n_{h}$, and stratum sample means \ (\overline{y}_{h}\). The population estimator $\hat{\overline{Y}}$ and the standard unbiased variance estimator $\nu(\hat{\overline{Y}})$ are

\begin{equation} \hat{\overline{Y}} =\sum_{h=1}^{H} W_{h}\overline{y}_{h}, \end{equation}

\begin{equation} \nu \left(\hat{\overline{Y}} \right) = \sum_{h=1}^{H} W_{h}^2 \frac{s_h^2}{n_{h}}, \end{equation}

with

\begin{equation} s^2_h=\frac{1}{n_{h}-1} \sum_{i=1}^{n_{h}} {(y_{h_{i}}-\overline{y}_{h})^2}. \end{equation}

The paired jackknife replicate variance estimator assigns one replicate $h=1,…,H$ to each stratum, so that the number of replicates equals $H$. In NAEP, the replicates correspond generally to pairs and triplets (with the latter only being used if there are an odd number of sample units within a particular primary stratum generating replicate strata). For pairs, the process of generating replicates can be viewed as taking a simple random sample $J$ of size $\frac{n_{h}}{2}$ within the replicate stratum, and assigning an increased weight to the sampled elements, and a decreased weight to the unsampled elements. In certain applications, the increased weight is double the full sample weight, while the decreased weight is in fact equal to zero. In this simplified case, this assignment reduces to replacing $\overline{y}_{h}$ with $\overline{y}_{h} (J)$, the latter being the sample mean of the sampled $\frac{n_{h}}{2}$ units. Then the replicate estimator corresponding to stratum $r$ is

\begin{equation} \hat{\overline{Y}}(r)=\sum_{h \ne r}^{H} W_{h} \overline{y}_h + W_r \overline{y}_h(J). \end{equation} The $r$-th term in the sum of squares for $\nu_{j} \left( \hat{\overline{Y}}\right)$ is thus

\begin{equation} \left( \hat{\overline{Y}}(r)- \hat{\overline{Y}} \right)^2 = W_r^2 \left( \overline{y}_r(J)- \overline{y}_r \right)^2. \end{equation}

In stratified random sampling, when a sample of size $\frac{n_r}{2}$ is drawn without replacement from a population of size $n_r$, the sampling variance is

\begin{equation} \begin{aligned} E \left( \overline{y}_{r’}(J)-\overline{y}_r \right)^2 = \frac {1} {\frac{n_r}{2} } \frac{ n_r - \frac{n_r}{2}} {n_r} \frac {1}{n_r-1}

\sum_{i=1}^{n_r} \left( y_{r_{i}} - \overline{y}_r \right)^2 \\ = \frac {1} {n_r \left( n_r-1 \right) } \sum_{i=1}^{n_r} \left( y_{r_{i}} - \overline{y}_r \right)^2 = \frac

{s^2_r}{n_r}. \end{aligned} \end{equation}

See for example Cochran (1977), Theorem 5.3, using $n_r$, as the “population size,” $\frac{n_r}{2}$as the “sample size,” and $s^2_r$ as the “population variance” in the given formula. Thus,

\begin{equation} E \left\{ W_r^2 \left( \overline{y}_{r}(J)- \overline{y}_r \right)^2 \right\} = W_r^2 \frac{s_r^2}{n_r}. \end{equation} Taking the expectation over all of these stratified samples of size $\frac{n_r}{2}$, it is found that

\begin{equation} E \left( \nu_j \left( \hat{\overline{Y}} \right) \right) =\nu \left( \hat{\overline{Y}}\right). \end{equation}

In this sense, the jackknife variance estimator "gives back" the sample variance estimator for means and totals as desired under the theory.

In cases where, rather than doubling the weight of one half of one variance stratum and assigning a zero weight to the other, the weight of one unit is multiplied by a replicate factor of $(1+\delta)$, while the other is multiplied by $(1-\delta)$, the result is that

\begin{equation} E \left( \hat{\overline{y}}(r)- \hat{\overline{y}} \right)^2 = W^2_r \delta^2 \frac{s^2_r}{n_r}. \end{equation}

In this way, by setting $\delta$ equal to the square root of the finite population correction factor, the jackknife variance estimator is able to incorporate a finite population correction factor into the variance estimator.

In practice, variance strata are also grouped to make sure that the number of replicates is not too large (the total number of variance strata is usually 62 for NAEP). The randomization from the original sample distribution guarantees that the sum of squares contributed by each replicate will be close to the target expected value.

For triples, the replicate factors are perturbed to something other than 1.0 for two different replicate factors, rather than just one as in the case of pairs. Again in the simple case where replicate factors that are less than 1 are all set to 0, the replicate weight factors are calculated as follows.

For unit $i$ in variance stratum $r$

\begin{equation} w_i(r) = \left\{\begin{array}{lll} 1.5w_i & i= \text{variance unit 1}\\ 1.5w_i & i= \text{variance unit 2}\\ 0 & i= \text{variance unit 3} \end{array}\right.

\end{equation}

where weight $w_i$ is the full sample base weight. Furthermore, for $r'=r+31$ $mod$ $62$

\begin{equation} w_i(r') = \left\{ \begin{array}{llll} 1.5w_i & i= \text{variance unit 1}\\ 0 & i= \text{variance unit 2}\\ 1.5w_i & i= \text{variance unit 3} \end{array}\right.

\end{equation}

And for all other values $r^*$, other than $r$ and $r'$, $w_i \left(r^*\right)=1$.

In the case of stratified random sampling, this formula reduces to replacing $\overline{y}_r$ with $\overline{y}_r(J)$ for replicate $r$, where $\overline{y}_r(J)$ is the sample mean from a "$2/3$" sample of $\frac{2n_r}{3}$ units from the $n_r$ sample units in the replicate stratum, and replacing $\overline{y}_r$ with $\overline{y}_{r'} (J)$ for replicate $r'$, where $\overline{y}_{r'}(J)$ is the sample mean from another overlapping "$2/3$" sample of $\frac{2n_r}{3}$ units from the $n_r$ sample units in the replicate stratum.

The $r$-th and $r'$-th replicates can be written as

\begin{equation} \hat{\overline{Y}}(r)=\sum_{h \ne r}^{H} W_{h} \overline{y}_h + W_r \overline{y}_r(J), \end{equation}

\begin{equation} \hat{\overline{Y}}(r')=\sum_{h \ne r}^{H} W_{h} \overline{y}_h + W_r \overline{y}_{r'}(J). \end{equation}

From these formulas, expressions for the $r$-th and $r'$-th components of the jackknife variance estimator are obtained (ignoring other sums of squares from other grouped components attached to those replicates):

\begin{equation} \left( \hat{\overline{Y}}(r)- \hat{\overline{Y}}\right)^2= W^2_r \left( \overline{y}_r(J)- \overline{y}_{r}\right)^2, \end{equation}

\begin{equation} \left( \hat{\overline{Y}}(r’)- \hat{\overline{Y}}\right)^2= W^2_r \left( \overline{y}_{r’}(J)- \overline{y}_{r}\right)^2. \end{equation} These sums of squares have expectations as follows, using the general formula for sampling variances:

\begin{equation} \begin{aligned} E\left( \overline{y}_r(J)- \overline{Y}_r\right)^2= \frac {1}{\frac{2n_r}{3}} \frac {n_r- \frac{2n_r}{3} }{n_r} \frac {1}{n_r-1}

\sum_{i=1}^{n_r} \left( y_{r_{i}} - \overline{y}_r \right)^2 \\ =\frac{1}{2n_r \left( n_r-1\right)} \sum_{i=1}^{n_r} \left( y_{r_{i}} - \overline{y}_r \right)^2 \\ =\frac

{s^2_r}{2n_r}, \end{aligned} \end{equation}

\begin{equation} \begin{aligned} E\left( \overline{y}_{r’}(J)- \overline{Y}_r\right)^2= \frac {1}{\frac{2n_r}{3}} \frac {n_r- \frac{2n_r}{3} }{n_r} \frac {1}{n_r-1}

\sum_{i=1}^{n_r} \left( y_{r_{i}} - \overline{y}_r \right)^2 \\ =\frac{1}{2n_r \left( n_r-1\right)} \sum_{i=1}^{n_r} \left( y_{r_{i}} - \overline{y}_r \right)^2 \\ =\frac

{s^2_r}{2n_r}. \end{aligned} \end{equation} Thus,

\begin{equation} \begin{aligned} E \left\{ W_r^2 \left( \overline{y}_r(J)- \overline{y}_r \right)^2 + W_r^2 \left( \overline{y}_{r’}(J)- \overline{y}_r \right)^2 \right\} \\ = W_r^2 \left( \frac {s^2_r}{2n_r} + \frac {s^2_r}{2n_r} \right) \\ = W_r^2 \frac {s^2_r}{n_r}, \end{aligned} \end{equation}

as desired again.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/replicate_variance_estimation_for_the_2022_assessment.aspx

Shape293

NAEP Technical Documentation Quality Control on Weighting Procedures

Given the complexity of the weighting procedures utilized in NAEP, a range of quality control (QC) checks was conducted throughout the weighting process to identify potential problems with collected student-level demographic data or with specific weighting procedures. The QC processes included:

checks performed within each step of the weighting process;

checks performed across adjacent steps of the weighting process; review of participation, exclusion, and accommodation rates;

checks of demographic data of individual schools and students;

comparisons with 2019 demographic data (or 2020 demographic data in the case of long-term trend [LTT]); and nonresponse bias analyses.

Final Participation, Exclusion, and Accommodation Rates

Nonresponse Bias Analyses

To validate the weighting process, extensive tabulations of various school and student characteristics at different stages of the process were conducted. The school-level characteristics included in the tabulations were racial/ethnic enrollment, median income (based on the school ZIP code area), and urban-centric locale. At the student level, the tabulations included race/ethnicity, gender, relative age, student disability (SD) status, English learner (EL) status, and participation status in National School Lunch Program (NSLP).

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/quality_control_on_weighting_procedures_for_the_2022_assessment.aspx

NAEP Technical Documentation Final Participation, Exclusion, and Accommodation Rates

Final participation, exclusion, and accommodation rates are presented in quality control tables for each grade (or age) and subject by geographic domain and school type. School- and student-level participation rates have been calculated according to National Center for Education Statistics (NCES) standards as they have been for previous assessments.

At the school level, private schools had participation rates below 85 percent in all grades (or ages) and subjects. At the student level, response rates at grade 8 fell below 85 percent for mathematics, reading, or both for the following state domains: Alaska, District of Columbia, Hawaii, New Hampshire, and New York; and the following TUDA domains: District of Columbia Public Schools, New

Grade 4 Mathematics

Grade 4 Reading

Grade 8 Mathematics

Grade 8 Reading

Grade 8 Civics Grade 8 U.S. History

York City, and Milwaukee. As required by NCES standards, nonresponse bias analyses were conducted on each reporting group falling below the 85 percent participation threshold.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/final_participation_exclusion_and_accommodation_rates_for_the_2022_assessment.aspx

Age 9 Mathematics

Age 9 Reading

Age 13 Mathematics

Age 13 Reading

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Age 13 Mathematics

The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the age 13 long-term trend mathematics assessment. Various weights were used in the calculation of the school rates, as indicated in the column headings of the table. For the student participation rates, student base weights were used. For the student exclusion rates and accommodation rates, student base weights with adjustment for school nonresponse were used. Different weights were used at the student level because the student participation rates are conditional on (i.e., computed within) the participating schools, whereas the exclusion and accommodation rates are population estimates.

The school participation rates reflect the participation of the original sampled schools only and do not reflect any effect of substitution. The rates weighted by the school base weight and enrollment show the approximate proportion of the student population in the domain that is represented by the responding schools in the sample. The rates weighted by just the base weight show the proportion of the school population that is represented by the responding schools in the sample. These rates differ because schools differ in size.

Participation, exclusion, and accommodation rates, age 13 long-term trend mathematics assessment, by school type and geographic region: 2022

School type and geographic region	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
National all¹	660	85.98	70.79	10,500	2.31	89.11	14.23
Northeast all	110	79.16	55.37	1,300	2.28	84.99	18.15
Midwest all	130	85.27	74.53	1,900	2.33	89.53	12.97
South all	260	87.71	72.78	4,500	1.79	90.17	16.62
West all	160	88.04	78.49	2,700	3.20	89.31	8.67
¹1¹National all includes national public, national private, and Department of Defense Education Activity (DoDEA) schools that are located in the United States.

NOTE: School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.

		School participation		School
Number of		rates (percent)		participation rates							Weighted
schools in		before substitution		(percent) before			Number of		Weighted		student
original		(weighted by base		substitution			students		percent of		participation	Weighted percent
sample,		weight and		(weighted by base			sampled,		students		rates (percent)	of students
School type and geographic region rounded		enrollment)		weight only)			rounded		excluded		after makeups	accommodated
National public	480		89.81		91.10	9,700		2.48		89.25			15.08
National private	180		40.35		33.24	800		0.29		85.77			4.21
Catholic	60		82.98		80.17	700		0.73		85.77			6.34
Non-Catholic	120		12.54		17.27	100		0.00		85.76			2.83

¹1¹National all includes national public, national private, and Department of Defense Education Activity (DoDEA) schools that are located in the United States. NOTE: School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_age_13_mathematics.aspx

Shape296

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Age 13 Reading

The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the age 13 long-term trend reading assessment. Various weights were used in the calculation of the school rates, as indicated in the column headings of the table. For the student participation rates student base weights were used. For the student exclusion rates and accommodation rates, student base weights with adjustment for school nonresponse were used. Different weights were used at the student level because the student participation rates are conditional on (i.e., computed within) the participating schools, whereas the exclusion and accommodation rates are population estimates.

Participation, exclusion, and accommodation rates, age 13 long-term trend reading assessment, by school type and geographic region: 2022

School type and geographic region	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
National all¹	660	85.98	70.79	10,500	3.08	89.22	13.08
Northeast all	110	79.16	55.37	1,300	4.64	83.90	14.83
Midwest all	130	85.27	74.53	1,900	1.61	89.71	13.16
South all	260	87.71	72.78	4,600	2.85	91.05	15.39
West all	160	88.04	78.49	2,700	3.91	88.66	7.65
National public	480	89.81	91.10	9,700	3.29	89.28	13.53
National private	180	40.35	33.24	800	0.66	87.68	7.92
Catholic	60	82.98	80.17	700	0.42	87.16	4.50
Non-Catholic	120	12.54	17.27	100	0.83	89.97	10.18
¹National all includes national public	, national priva	te, and Department of	Defense Education Ac	tivity (DoDEA)	schools that ar	e located in the Un	ited States.

NOTE: School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_age_13_reading.aspx

Shape297

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Age 9 Mathematics

The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the age 9 long-term trend mathematics assessment. Various weights were used in the calculation of the school rates, as indicated in the column headings of the table. For the student participation rates, student base weights were used. For the student exclusion rates and accommodation rates, student base weights with adjustment for school nonresponse were used. Different weights were used at the student level because the student participation rates are conditional on (i.e., computed within) the participating schools, whereas the exclusion and accommodation rates are population estimates.

Participation, exclusion, and accommodation rates, age 9 long-term trend mathematics assessment, by school type and geographic region: 2022

School type and geographic region	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
National all¹	580	85.93	72.56	9,200	1.87	87.08	14.95
Northeast all	90	86.73	63.95	1,300	2.93	83.10	16.41
Midwest all	110	74.94	72.78	1,500	1.37	87.78	13.55
South all	240	93.22	79.44	4,300	1.59	88.44	19.57
West all	140	82.42	68.64	2,200	2.11	86.69	7.81
National public	410	90.45	88.79	8,700	2.02	86.96	16.00
National private	160	32.02	28.98	500	0.12	90.42	2.82
Catholic	50	62.73	60.99	400	0.31	93.25	2.37
Non-Catholic	120	13.88	19.13	100	0.00	84.02	3.09
¹1¹^National^all^includes^national^public,^national^private,^and^Department^of^Defense^Education^Activity^(DoDEA)^schools^that^are^locatedⁱⁿ^the^United^States.

NOTE: School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_age_9_mathematics.aspx

Shape298

NAEP Technical DocumentationParticipation, Exclusion, and Accommodation Rates for Age 9 Reading

The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the age 9 long-term trend reading assessment. Various weights were used in the calculation of the school rates, as indicated in the column headings of the table. For the student participation rates student base weights were used. For the student exclusion rates and accommodation rates, student base weights with adjustment for school nonresponse were used. Different weights were used at the student level because the student participation rates are conditional on (i.e., computed within) the participating schools, whereas the exclusion and accommodation rates are population estimates.

by just the base weight show the proportion of the school population that is represented by the responding schools in the sample. These rates differ because schools differ in size.

Participation, exclusion, and accommodation rates, age 9 long-term trend reading assessment, by school type and geographic region: 2022

School type and geographic region	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
National all¹	580	85.93	72.56	9,200	2.34	87.13	14.18
Northeast all	90	86.73	63.95	1,300	1.90	82.35	18.66
Midwest all	110	74.94	72.78	1,500	1.20	89.58	14.13
South all	240	93.22	79.44	4,300	2.71	87.94	16.53
West all	140	82.42	68.64	2,200	3.05	86.99	7.52
National public	410	90.45	88.79	8,700	2.52	87.00	15.13
National private	160	32.02	28.98	500	0.22	90.89	3.20
Catholic	50	62.73	60.99	400	0.59	92.30	3.29
Non-Catholic	120	13.88	19.13	100	0.00	87.70	3.15
¹1¹^National^all^includes^national^pub	lic, national pr	ivate, and Department	of Defense Education	Activity (DoDE	A) schools that	are located in the	United States.

NOTE: School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_age_9_reading.aspx

Shape299

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 4 Mathematics

The following table displays the school- and student-level response, exclusion, and accommodation rates for the grade 4 mathematics assessment by school type and jurisdiction. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.

The participation rates reflect the participation of the original sample schools only and do not reflect any effect of substitution. The rates weighted by the base weight and enrollment show the approximate proportion of the student population in the jurisdiction that is represented by the responding schools in the sample. The rates weighted by just the base weight show the proportion of the school population that is represented by the responding schools in the sample. These rates differ because schools differ in size.

Participation, exclusion, and accommodation rates, grade 4 mathematics combined national and state assessment, by school type and jurisdiction: 2022

School type and jurisdiction	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
All	6,410	94.48	82.93	139,400	1.81	91.86	14.27
National all¹	6,260	94.45	82.79	135,800	1.81	91.85	14.19
Northeast all	1,060	91.11	76.06	21,700	1.74	90.47	17.74
Midwest all	1,460	95.32	85.44	29,400	1.33	92.18	12.95
South all	2,170	94.70	82.26	50,600	2.12	92.51	16.69
West all	1,500	95.54	85.60	31,900	1.78	91.39	8.73
National public	5,750	99.53	99.54	130,900	1.94	91.79	14.93
Alabama	90	100.00	100.00	2,200	1.27	94.68	10.42
Alaska	130	99.20	93.50	2,100	1.01	88.61	16.83
Arizona	90	100.00	100.00	2,200	1.28	92.83	11.27
Arkansas	90	100.00	100.00	2,000	0.97	92.58	21.24
California	190	100.00	100.00	4,500	2.22	91.91	7.38
Colorado	120	99.04	98.43	2,900	1.76	91.10	11.74
Connecticut	90	100.00	100.00	2,100	2.46	91.79	17.50
Delaware	80	100.00	100.00	2,200	1.74	91.03	17.15
District of Columbia	90	100.00	100.00	2,100	2.25	88.24	25.53
Florida	210	100.00	100.00	5,400	2.69	91.80	21.68
Georgia	120	96.17	96.07	3,100	1.40	92.84	15.03
Hawaii	90	100.00	100.00	2,200	1.62	88.53	6.55
Idaho	90	100.00	100.00	2,000	0.92	93.22	10.07
Illinois	150	100.00	100.00	3,200	1.32	91.19	19.24
Indiana	90	98.63	99.22	2,000	0.45	92.77	19.67
Iowa	90	98.67	99.41	2,100	1.42	93.08	13.54
Kansas	100	100.00	100.00	2,100	1.43	92.88	10.00
Kentucky	120	100.00	100.00	2,700	1.93	94.50	16.61
¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools,^but^not^schoolsⁱⁿPuerto Rico. ²2²Department of Defense Education Activity schools.

NOTE: Numbers of schools are rounded to nearest ten, and numbers of students are rounded to nearest hundred. Detail may not sum to totals due to rounding. SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2022 Mathematics Assessment.

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)	Number of	Weighted	Weighted student
original		(weighted by base		before substitution	students	percent of	participation		Weighted percent
sample,		weight and		(weighted by base	sampled,	students	rates (percent)		of students
School type and jurisdiction rounded		enrollment)		weight only)	rounded	excluded	after makeups		accommodated
Louisiana	90		100.00	100.00	2,100	1.60	92.36	19.32
Maine	110		100.00	100.00	2,000	1.51	90.46	15.87
Maryland	120		100.00	100.00	3,000	1.37	92.09	21.26
Massachusetts	130		100.00	100.00	3,100	1.91	92.84	18.33
Michigan	140		100.00	100.00	3,100	2.93	91.18	7.97
Minnesota	90		100.00	100.00	2,300	2.47	90.79	10.38
Mississippi	90		100.00	100.00	2,200	0.76	92.78	13.96
Missouri	100		100.00	100.00	2,000	0.92	94.35	12.21
Montana	130		99.95	98.56	2,100	1.00	89.77	10.64
Nebraska	100		100.00	100.00	2,200	1.23	94.76	14.14
Nevada	100		100.00	100.00	2,400	1.70	92.26	6.13
New Hampshire	100		99.15	98.79	2,200	1.28	86.89	15.94
New Jersey	90		98.72	98.91	2,000	2.03	92.15	20.06
New Mexico	120		100.00	100.00	2,600	1.58	90.58	15.72
New York	120		95.76	95.82	2,900	1.22	86.46	21.33
North Carolina	160		100.00	100.00	4,100	1.98	90.96	13.47
North Dakota	120		99.28	97.26	2,200	1.28	90.24	11.59
Ohio	140		100.00	100.00	2,800	1.21	92.78	16.60
Oklahoma	100		100.00	100.00	2,100	2.21	93.65	16.15
Oregon	90		100.00	100.00	2,200	1.55	87.89	10.17
Pennsylvania	120		99.86	99.93	3,000	2.02	92.53	14.36
Rhode Island	90		100.00	100.00	2,100	1.61	94.25	17.33
South Carolina	90		100.00	100.00	2,100	1.11	93.01	12.09
South Dakota	120		100.00	100.00	2,100	1.13	93.78	9.42
Tennessee	120		100.00	100.00	2,800	2.39	92.04	14.05
Texas	270		100.00	100.00	6,800	3.09	92.75	19.43
Utah	90		100.00	100.00	2,200	1.10	92.24	11.54
Vermont	130		100.00	100.00	2,100	1.41	88.80	16.41

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)	Number of	Weighted		Weighted student
original		(weighted by base		before substitution	students	percent of		participation	Weighted percent
sample,		weight and		(weighted by base	sampled,	students		rates (percent)	of students
School type and jurisdiction rounded		enrollment)		weight only)	rounded	excluded		after makeups	accommodated
Virginia	90		100.00	100.00	2,200		2.79	91.98		14.14
Washington	90		100.00	100.00	2,200		2.15	89.21		10.33
West Virginia	100		100.00	100.00	2,100		1.59	92.64		11.28
Wisconsin	130		100.00	100.00	2,700		1.29	90.27		12.14
Wyoming	100		98.78	99.16	2,100		1.27	90.11		13.57
Trial Urban (TUDA) Districts
Albuquerque	40		100.00	100.00	1,100		0.56	91.29		18.75
Atlanta	40		100.00	100.00	1,100		0.87	93.69		12.51
Austin	40		100.00	100.00	1,200		3.08	87.96		30.02
Baltimore City	50		100.00	100.00	1,000		1.39	89.82		26.15
Boston	50		100.00	100.00	1,100		5.73	90.83		19.29
Charlotte-Mecklenburg	40		100.00	100.00	1,100		2.23	92.44		12.53
Chicago	70		100.00	100.00	1,500		2.85	90.39		23.41
Clark County (NV)	60		100.00	100.00	1,600		1.16	92.17		5.76
Cleveland	50		100.00	100.00	900		2.55	88.77		24.26
Dallas	40		100.00	100.00	1,000		4.26	91.71		38.46
Denver	40		100.00	100.00	1,100		2.16	88.86		15.39
Detroit	40		100.00	100.00	1,100		4.11	89.97		7.55
Duval County (FL)	40		100.00	100.00	1,100		2.07	91.75		23.97
Fort Worth	40		100.00	100.00	1,100		2.26	93.11		18.16
Guilford County (NC)	40		100.00	100.00	1,100		1.46	92.62		15.31
Hillsborough County (FL)	40		100.00	100.00	1,100		3.14	92.13		23.08
Houston	60		100.00	100.00	1,600		3.22	93.43		22.76
Jefferson County (KY)	40		100.00	100.00	1,000		3.58	93.68		22.10
Los Angeles	60		100.00	100.00	1,600		1.98	91.97		10.61
Miami	60		100.00	100.00	1,600		3.08	94.64		25.04
Milwaukee	50		100.00	100.00	1,000		1.45	86.42		22.28
New York City	70		98.73	98.87	1,600		1.26	87.37		27.52

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)	Number of	Weighted		Weighted student
original		(weighted by base		before substitution	students	percent of		participation		Weighted percent
sample,		weight and		(weighted by base	sampled,	students		rates (percent)		of students
School type and jurisdiction rounded		enrollment)		weight only)	rounded	excluded		after makeups		accommodated
Philadelphia	40	98.11	99.29		1,000		4.32		93.65	21.07
San Diego	40	100.00	100.00		1,000		2.92		88.61	12.46
Shelby County (TN)	40	100.00	100.00		1,000		3.73		94.05	14.79
District of Columbia (DCPS)	50	100.00	100.00		1,300		3.30		89.57	30.10
National private	390	37.50	33.92		1,800		0.48		93.71	5.98
Catholic	120	66.61	68.59		1,100		0.37		93.67	7.03
Non-Catholic	270	20.01	20.37		700		0.54		93.77	5.36
Other jurisdictions
DoDEA²	100	94.55	92.13		3,000		1.68		88.71	17.62
Puerto Rico	150	100.00	100.00		3,500		0.16		92.19	31.52

¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools,^but^not^schoolsⁱⁿPuerto Rico.

²2²Department of Defense Education Activity schools.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_grade_4_mathematics_for_the_2022_assessment.aspx

Shape304

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 4 Reading

The following table displays the school- and student-level response, exclusion, and accommodation rates for the grade 4 reading assessment by school type and jurisdiction. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.

Participation, exclusion, and accommodation rates, grade 4 reading combined national and state assessment, by school type and jurisdiction: 2022

School type and jurisdiction	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
All	6,260	94.45	82.79	127,000	1.96	91.70	14.09
National all¹	6,260	94.45	82.79	127,000	1.96	91.70	14.09
Northeast all	1,060	91.11	76.06	20,400	2.14	90.18	16.94
Midwest all	1,460	95.32	85.44	27,600	1.44	92.11	12.57
South all	2,170	94.70	82.26	47,200	2.22	92.36	16.86
West all	1,500	95.54	85.60	29,900	1.85	91.23	8.89
National public	5,750	99.53	99.54	122,400	2.11	91.61	14.86
Alabama	90	100.00	100.00	2,000	1.14	93.53	11.45
Alaska	130	99.20	93.50	2,000	0.61	88.73	18.28
Arizona	90	100.00	100.00	2,100	1.21	92.25	11.39
Arkansas	90	100.00	100.00	1,900	1.69	93.87	19.84
California	190	100.00	100.00	4,200	2.30	91.45	7.91
Colorado	120	99.04	98.43	2,700	2.67	91.37	10.85
Connecticut	90	100.00	100.00	2,000	2.51	88.93	17.72
Delaware	80	100.00	100.00	2,000	1.33	89.69	18.24
District of Columbia	90	100.00	100.00	1,900	4.17	87.75	23.07
Florida	210	100.00	100.00	5,000	2.37	93.05	22.65
Georgia	120	96.17	96.07	3,000	1.82	92.18	16.21
Hawaii	90	100.00	100.00	2,000	1.24	88.58	6.03
Idaho	90	100.00	100.00	1,900	1.72	92.45	10.09
Illinois	150	100.00	100.00	3,000	0.92	90.91	18.44
Indiana	90	98.63	99.22	1,900	0.68	93.09	19.87
Iowa	90	98.67	99.41	2,000	1.18	92.99	14.86
Kansas	100	100.00	100.00	1,900	0.97	93.24	10.40
Kentucky	120	100.00	100.00	2,600	3.07	93.45	16.12
Louisiana	90	100.00	100.00	1,900	2.39	92.12	17.91
¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools. ²2²Department of Defense Education Activity schools.

			School participation
Number of			rates (percent) before		School participation
schools in			substitution		rates (percent)		Number of	Weighted			Weighted student
original			(weighted by base		before substitution		students	percent of			participation	Weighted percent
sample,			weight and		(weighted by base		sampled,	students			rates (percent)	of students
School type and jurisdiction rounded			enrollment)		weight only)		rounded	excluded			after makeups	accommodated
Maine	110	100.00		100.00		1,900			1.02	92.02			16.34
Maryland	120	100.00		100.00		2,800			1.93	91.81			21.34
Massachusetts	130	100.00		100.00		2,900			2.48	92.98			16.39
Michigan	140	100.00		100.00		2,900			2.56	90.98			8.10
Minnesota	90	100.00		100.00		2,100			3.54	91.18			10.29
Mississippi	90	100.00		100.00		2,000			1.31	92.70			13.47
Missouri	100	100.00		100.00		2,000			0.84	93.38			12.72
Montana	130	99.95		98.56		2,000			1.32	89.73			11.56
Nebraska	100	100.00		100.00		2,000			1.29	94.33			14.01
Nevada	100	100.00		100.00		2,300			1.52	91.47			7.40
New Hampshire	100	99.15		98.79		2,000			1.15	87.70			16.10
New Jersey	90	98.72		98.91		1,900			2.84	91.90			19.03
New Mexico	120	100.00		100.00		2,400			1.38	91.03			14.56
New York	120	95.76		95.82		2,700			2.23	86.57			19.98
North Carolina	160	100.00		100.00		3,800			1.86	91.11			13.85
North Dakota	120	99.28		97.26		2,100			1.70	91.16			11.76
Ohio	140	100.00		100.00		2,700			2.40	92.35			14.63
Oklahoma	100	100.00		100.00		1,900			1.67	92.40			16.62
Oregon	90	100.00		100.00		2,100			1.85	89.66			9.65
Pennsylvania	120	99.86		99.93		2,800			2.12	91.83			14.50
Rhode Island	90	100.00		100.00		2,000			1.19	93.82			17.68
South Carolina	90	100.00		100.00		2,000			1.67	92.09			12.06
South Dakota	120	100.00		100.00		2,000			1.04	93.95			9.33
Tennessee	120	100.00		100.00		2,700			2.14	91.68			14.13
Texas	270	100.00		100.00		6,400			3.28	92.44			19.82
Utah	90	100.00		100.00		2,000			1.03	92.30			10.55
Vermont	130	100.00		100.00		2,000			1.27	89.00			16.55
Virginia	90	100.00		100.00		2,000			2.25	91.86			12.33

			School participation
Number of			rates (percent) before		School participation
schools in			substitution		rates (percent)	Number of	Weighted	Weighted student
original			(weighted by base		before substitution	students	percent of	participation			Weighted percent
sample,			weight and		(weighted by base	sampled,	students	rates (percent)			of students
School type and jurisdiction rounded			enrollment)		weight only)	rounded	excluded	after makeups			accommodated
Washington	90	100.00		100.00		2,000	1.72		88.85	9.78
West Virginia	100	100.00		100.00		1,900	1.66		90.27	10.12
Wisconsin	130	100.00		100.00		2,600	0.99		90.73	12.33
Wyoming	100	98.78		99.16		2,000	1.72		91.74	14.36
Trial Urban (TUDA) Districts
Albuquerque	40	100.00		100.00		1,000	1.34		91.29	17.90
Atlanta	40	100.00		100.00		1,000	2.76		92.78	11.45
Austin	40	100.00		100.00		1,100	5.14		89.14	28.32
Baltimore City	50	100.00		100.00		1,000	3.23		90.67	25.26
Boston	50	100.00		100.00		1,000	6.09		90.96	16.80
Charlotte-Mecklenburg	40	100.00		100.00		1,000	1.70		91.77	10.12
Chicago	70	100.00		100.00		1,400	2.26		89.02	23.88
Clark County (NV)	60	100.00		100.00		1,500	1.71		91.94	7.07
Cleveland	50	100.00		100.00		900	2.11		87.53	25.20
Dallas	40	100.00		100.00		1,000	4.18		92.41	38.31
Denver	40	100.00		100.00		1,000	3.17		90.68	13.12
Detroit	40	100.00		100.00		1,000	4.21		89.44	6.40
Duval County (FL)	40	100.00		100.00		1,000	2.08		93.11	24.16
Fort Worth	40	100.00		100.00		1,000	3.22		91.01	17.14
Guilford County (NC)	40	100.00		100.00		1,000	1.71		91.77	13.07
Hillsborough County (FL)	40	100.00		100.00		1,000	3.03		93.93	22.59
Houston	60	100.00		100.00		1,500	2.28		92.05	23.97
Jefferson County (KY)	40	100.00		100.00		1,000	6.31		92.34	17.78
Los Angeles	60	100.00		100.00		1,500	2.18		92.38	12.00
Miami	60	100.00		100.00		1,500	2.92		92.83	24.82
Milwaukee	50	100.00		100.00		900	2.32		85.33	21.67
New York City	70	98.73		98.87		1,500	2.32		87.42	26.42
Philadelphia	40	98.11		99.29		1,000	6.60		93.38	18.23

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)		Number of	Weighted			Weighted student
original		(weighted by base		before substitution		students	percent of			participation	Weighted percent
sample,		weight and		(weighted by base		sampled,	students			rates (percent)	of students
School type and jurisdiction rounded		enrollment)		weight only)		rounded	excluded			after makeups	accommodated
San Diego	40	100.00	100.00		900			2.75	88.59			12.38
Shelby County (TN)	40	100.00	100.00		1,000			3.82	91.22			14.68
District of Columbia (DCPS)	50	100.00	100.00		1,200			5.69	88.64			26.20
National private	390	37.50	33.92		1,600			0.25	94.12			5.49
Catholic	120	66.61	68.59		1,000			0.38	95.19			6.15
Non-Catholic	270	20.01	20.37		600			0.17	92.19			5.09
Other jurisdictions
DoDEA²	100	94.55	92.13		2,900			1.72	89.71			17.96

¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools.

²2²Department of Defense Education Activity schools.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_grade_4_reading_for_the_2022_assessment.aspx

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 Civics

The following table displays the school- and student-level response, exclusion, and accommodation rates for the grade 8 civics assessment. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.

The participation rates reflect the participation of the original sample schools only and do not reflect any effect of substitution. The rates weighted by the base weight and enrollment show the approximate proportion of the student population in the school type and geographic region that is represented by the responding schools in the sample. The rates weighted by just the base weight show the proportion of the school population that is represented by the responding schools in the sample. These rates differ because schools differ in size.

Participation, exclusion, and accommodation rates, grade 8 civics national assessment, by school type and geographic region: 2022

School type and geographic region	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
All	570	86.62	69.97	9,400	1.52	90.05	13.25
National all¹	570	86.62	69.97	9,400	1.52	90.05	13.25
Northeast all	90	82.11	60.26	1,200	1.36	88.37	17.65
Midwest all	110	87.34	71.53	1,800	1.39	91.26	13.01
South all	230	91.46	73.39	4,200	1.51	90.52	14.91
West all	140	80.38	69.74	2,100	1.77	88.99	7.73
National public	400	91.00	91.88	8,800	1.65	89.96	14.04
National private	170	33.59	33.24	600	0.00	92.30	4.12
Catholic	40	61.74	74.36	400	0.00	91.89	5.34
Non-Catholic	130	15.03	17.71	200	0.00	93.55	3.32
¹1¹^Includes^national^public,^national^private,^and^Department^of^Defense^Education^Activity^schools^locatedⁱⁿ^the^United^States.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_grade_8_civics_for_the_2022_assessment.aspx

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 Mathematics

The following table displays the school- and student-level response, exclusion, and accommodation rates for the grade 8 mathematics assessment by school type and jurisdiction. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.

Participation, exclusion, and accommodation rates, grade 8 mathematics combined national and state assessment, by school type and jurisdiction: 2022

School type and jurisdiction	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
All	5,870	94.69	74.55	138,700	1.53	88.87	13.75
National all¹	5,730	94.67	74.35	135,100	1.54	88.86	13.67
Northeast all	950	91.21	62.39	21,700	1.57	86.65	17.75
Midwest all	1,370	95.37	77.07	29,700	1.16	89.24	12.52
South all	2,000	95.51	75.16	50,100	1.65	90.00	15.17
West all	1,350	94.96	80.42	32,000	1.69	88.01	9.45
National public	5,280	99.61	99.50	131,300	1.67	88.68	14.42
Alabama	90	100.00	100.00	2,100	1.64	91.21	9.15
Alaska	110	98.71	93.92	2,000	1.05	83.79	14.47
Arizona	90	100.00	100.00	2,100	1.67	90.30	9.94
Arkansas	90	100.00	100.00	2,200	0.98	91.18	19.69
California	180	100.00	100.00	4,400	2.16	88.05	8.73
Colorado	120	96.76	95.47	2,800	1.36	86.46	10.41
Connecticut	90	98.77	97.80	2,000	1.69	87.84	17.79
Delaware	50	100.00	100.00	2,100	1.90	87.27	17.75
District of Columbia	80	100.00	100.00	2,000	2.74	82.67	25.65
Florida	210	100.00	100.00	5,400	2.56	89.47	22.03
Georgia	110	100.00	100.00	3,100	1.75	90.25	16.63
Hawaii	50	100.00	100.00	2,200	1.99	85.29	4.37
Idaho	90	100.00	100.00	2,200	1.22	90.48	11.37
Illinois	140	100.00	100.00	3,300	1.12	87.95	16.25
Indiana	90	98.83	99.41	2,000	0.73	90.54	18.17
Iowa	90	100.00	100.00	2,100	1.48	90.13	15.07
Kansas	90	100.00	100.00	2,200	1.32	91.03	10.74
Kentucky	110	100.00	100.00	2,800	2.32	89.43	14.25
Louisiana	90	100.00	100.00	2,100	2.28	89.70	20.14
Maine	90	97.56	96.39	2,100	0.99	86.84	18.58
¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools,^but^not^schoolsⁱⁿPuerto Rico. ²2²Department of Defense Education Activity schools.

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)		Number of		Weighted		Weighted student
original		(weighted by base		before substitution		students		percent of		participation		Weighted percent
sample,		weight and		(weighted by base		sampled,		students		rates (percent)		of students
School type and jurisdiction rounded		enrollment)		weight only)		rounded		excluded		after makeups		accommodated
Maryland	130		100.00		100.00		3,000		1.82		89.06		18.06
Massachusetts	130		100.00		100.00		3,000		2.62		87.89		17.83
Michigan	130		100.00		100.00		3,000		1.80		86.82		10.49
Minnesota	100		98.62		99.16		1,900		2.08		85.74		8.79
Mississippi	90		100.00		100.00		2,200		0.84		90.09		12.25
Missouri	100		100.00		100.00		2,200		0.99		91.73		11.54
Montana	100		99.95		98.06		2,100		1.17		85.81		12.23
Nebraska	100		100.00		100.00		2,200		1.76		92.46		12.69
Nevada	90		100.00		100.00		2,400		1.10		87.92		6.89
New Hampshire	80		98.97		98.63		2,100		1.48		82.00		12.45
New Jersey	90		98.85		99.47		2,100		1.61		91.20		19.77
New Mexico	100		100.00		100.00		2,700		1.67		88.36		14.40
New York	130		97.65		97.92		2,900		1.65		81.09		20.63
North Carolina	140		100.00		100.00		3,900		1.14		90.32		13.01
North Dakota	90		100.00		100.00		2,100		1.38		88.51		12.28
Ohio	140		100.00		100.00		2,900		1.11		89.59		16.08
Oklahoma	90		100.00		100.00		2,100		1.61		92.11		14.99
Oregon	90		100.00		100.00		2,100		1.51		84.92		10.91
Pennsylvania	120		99.42		99.75		2,900		1.35		89.04		16.94
Rhode Island	60		100.00		100.00		2,100		2.22		90.48		16.63
South Carolina	90		100.00		100.00		2,100		1.47		91.36		10.12
South Dakota	100		98.95		98.85		2,200		1.62		91.16		6.87
Tennessee	120		97.51		96.30		3,000		2.30		90.98		12.11
Texas	220		100.00		100.00		6,600		1.56		89.72		15.94
Utah	90		100.00		100.00		2,200		1.67		87.70		12.50
Vermont	90		100.00		100.00		2,200		1.72		87.05		16.37
Virginia	90		98.75		99.52		2,100		1.70		88.42		12.39
Washington	90		100.00		100.00		2,200		1.37		86.92		10.88

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)			Number of	Weighted		Weighted student
original		(weighted by base		before substitution			students	percent of		participation			Weighted percent
sample,		weight and		(weighted by base			sampled,	students		rates (percent)			of students
School type and jurisdiction rounded		enrollment)		weight only)			rounded	excluded		after makeups			accommodated
West Virginia	90		100.00		100.00	2,200			1.52		90.99	11.68
Wisconsin	130		100.00		100.00	3,100			1.26		87.83	12.25
Wyoming	70		100.00		100.00	2,200			1.41		87.33	11.99
Trial Urban (TUDA) Districts
Albuquerque	30		100.00		100.00	1,100			1.92		85.50	15.81
Atlanta	30		100.00		100.00	1,000			0.90		90.39	19.32
Austin	20		100.00		100.00	1,100			1.94		84.80	25.07
Baltimore City	50		100.00		100.00	1,000			2.86		90.04	21.19
Boston	50		100.00		100.00	1,000			5.94		88.86	19.68
Charlotte-Mecklenburg	30		100.00		100.00	1,100			3.11		89.89	11.80
Chicago	70		100.00		100.00	1,600			0.95		88.15	25.00
Clark County (NV)	50		100.00		100.00	1,600			1.29		85.93	7.37
Cleveland	50		100.00		100.00	900			3.82		87.12	21.92
Dallas	40		100.00		100.00	1,100			2.21		91.02	22.29
Denver	40		92.34		98.48	1,000			2.70		87.68	13.03
Detroit	40		100.00		100.00	1,000			5.02		88.79	11.55
Duval County (FL)	40		100.00		100.00	1,100			1.53		91.37	21.43
Fort Worth	30		100.00		100.00	1,000			2.24		91.81	14.09
Guilford County (NC)	30		100.00		100.00	1,000			1.77		89.25	14.89
Hillsborough County (FL)	40		100.00		100.00	1,100			2.25		90.53	21.08
Houston	40		100.00		100.00	1,500			3.03		88.66	15.70
Jefferson County (KY)	30		100.00		100.00	1,100			1.46		91.05	15.00
Los Angeles	60		100.00		100.00	1,600			2.33		88.71	9.72
Miami	70		100.00		100.00	1,600			3.57		91.25	18.20
Milwaukee	40		100.00		100.00	1,100			2.12		80.38	23.55
New York City	70		96.75		95.00	1,600			0.69		83.59	25.12
Philadelphia	40		91.14		98.36	1,000			4.47		86.81	20.70
San Diego	40		100.00		100.00	1,000			1.80		85.52	12.45

			School participation
Number of			rates (percent) before		School participation
schools in			substitution		rates (percent)	Number of	Weighted		Weighted student
original			(weighted by base		before substitution	students	percent of		participation			Weighted percent
sample,			weight and		(weighted by base	sampled,	students		rates (percent)			of students
School type and jurisdiction rounded			enrollment)		weight only)	rounded	excluded		after makeups			accommodated
Shelby County (TN)	40	100.00		100.00		1,100		2.77		90.34	9.39
District of Columbia (DCPS)	30	100.00		100.00		1,000		3.94		81.92	27.63
National private	380	35.49		32.62		1,600		0.00		93.97	4.84
Catholic	110	60.98		65.94		1,000		0.00		94.09	6.83
Non-Catholic	270	19.80		20.04		600		0.00		93.74	3.61
Other jurisdictions DoDEA²	60	94.14		86.27		2,100		1.12		89.55	13.29
Puerto Rico	150	100.00		100.00		3,600		0.06		91.07	30.04

¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools,^but^not^schoolsⁱⁿPuerto Rico.

²2²Department of Defense Education Activity schools.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_grade_8_mathematics_for_the_2022_assessment.aspx

Shape329

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 Reading

The following table displays the school- and student-level response, exclusion, and accommodation rates for the grade 8 reading assessment by school type and jurisdiction. Various weights were used in the calculation of the rates, as indicated in the column headings of the table. The participation rates reflect the participation of the original sample schools only and do not reflect any effect of substitution. The rates weighted by the base weight and enrollment show the approximate proportion of the student population in the jurisdiction that is represented by the responding schools in the sample. The rates weighted by just the base weight show the proportion of the school population that is represented by the responding schools in the sample. These rates differ because schools differ in size.

Participation, exclusion, and accommodation rates, grade 8 reading combined national and state assessment, by school type and jurisdiction: 2022

School type and jurisdiction	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
All	5,730	94.67	74.35	135,200	1.75	89.02	13.19
National all¹	5,730	94.67	74.35	135,200	1.75	89.02	13.19
Northeast all	950	91.21	62.39	21,700	1.95	86.87	17.51
Midwest all	1,370	95.37	77.07	29,800	1.13	89.30	11.91
South all	2,000	95.51	75.16	50,100	1.95	90.39	14.72
West all	1,350	94.96	80.42	32,000	1.86	87.84	8.90
National public	5,280	99.61	99.50	131,400	1.89	88.82	13.86
Alabama	90	100.00	100.00	2,100	0.98	92.41	9.08
Alaska	110	98.71	93.92	2,100	0.48	82.03	15.08
Arizona	90	100.00	100.00	2,100	1.77	89.78	9.41
Arkansas	90	100.00	100.00	2,200	1.63	91.43	18.33
California	180	100.00	100.00	4,400	2.48	88.09	7.74
Colorado	120	96.76	95.47	2,800	1.95	86.94	10.67
Connecticut	90	98.77	97.80	2,100	1.77	88.43	16.40
Delaware	50	100.00	100.00	2,100	1.49	87.58	18.91
District of Columbia	80	100.00	100.00	2,000	3.07	83.75	24.58
Florida	210	100.00	100.00	5,400	2.34	87.36	22.00
Georgia	110	100.00	100.00	3,100	1.97	92.79	16.63
Hawaii	50	100.00	100.00	2,200	1.56	83.42	4.96
Idaho	90	100.00	100.00	2,200	1.83	91.03	10.68
Illinois	140	100.00	100.00	3,300	1.28	88.38	15.29
Indiana	90	98.83	99.41	2,000	0.51	90.34	16.35
Iowa	90	100.00	100.00	2,100	1.18	90.16	15.87
Kansas	90	100.00	100.00	2,200	1.37	92.93	9.85
Kentucky	110	100.00	100.00	2,800	2.05	91.10	14.91
Louisiana	90	100.00	100.00	2,100	2.85	89.24	18.44
Maine	90	97.56	96.39	2,100	1.32	89.52	18.39
Maryland	130	100.00	100.00	3,000	1.87	90.36	18.17
¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools. ²2²Department of Defense Education Activity schools.

		School participation
Number of		rates (percent) before		School participation
schools in		substitution		rates (percent)		Number of			Weighted	Weighted student
original		(weighted by base		before substitution		students			percent of	participation			Weighted percent
sample,		weight and		(weighted by base		sampled,			students	rates (percent)			of students
School type and jurisdiction rounded		enrollment)		weight only)		rounded			excluded	after makeups			accommodated
Massachusetts	130		100.00		100.00		3,000	2.80			88.83	16.89
Michigan	130		100.00		100.00		3,000	1.54			86.24	11.11
Minnesota	100		98.62		99.16		1,900	1.95			84.69	8.52
Mississippi	90		100.00		100.00		2,200	0.68			91.75	12.96
Missouri	100		100.00		100.00		2,200	1.20			92.49	10.61
Montana	100		99.95		98.06		2,100	0.84			87.24	11.73
Nebraska	100		100.00		100.00		2,200	1.43			92.69	11.41
Nevada	90		100.00		100.00		2,400	1.13			88.06	5.09
New Hampshire	80		98.97		98.63		2,100	1.04			84.57	12.87
New Jersey	90		98.85		99.47		2,100	2.24			89.50	19.35
New Mexico	100		100.00		100.00		2,700	1.69			87.17	12.68
New York	130		97.65		97.92		2,900	2.21			81.82	20.55
North Carolina	140		100.00		100.00		4,000	1.90			89.15	12.43
North Dakota	90		100.00		100.00		2,100	1.53			88.82	11.96
Ohio	140		100.00		100.00		2,900	1.39			89.39	15.95
Oklahoma	90		100.00		100.00		2,100	2.35			92.72	12.65
Oregon	90		100.00		100.00		2,100	0.88			85.28	10.92
Pennsylvania	120		99.42		99.75		2,900	1.72			89.13	17.47
Rhode Island	60		100.00		100.00		2,100	1.69			89.57	17.35
South Carolina	90		100.00		100.00		2,100	1.35			92.35	11.20
South Dakota	100		98.95		98.85		2,200	1.75			91.64	5.95
Tennessee	120		97.51		96.30		2,900	2.69			89.14	11.95
Texas	220		100.00		100.00		6,600	2.19			90.81	14.66
Utah	90		100.00		100.00		2,200	1.31			87.55	12.96
Vermont	90		100.00		100.00		2,200	1.67			86.98	16.15
Virginia	90		98.75		99.52		2,100	2.45			89.02	10.22
Washington	90		100.00		100.00		2,200	1.54			85.49	9.42
West Virginia	90		100.00		100.00		2,200	1.73			90.88	10.09

		School participation
Number of		rates (percent) before			School participation
schools in		substitution			rates (percent)	Number of	Weighted		Weighted student
original		(weighted by base			before substitution	students	percent of		participation			Weighted percent
sample,		weight and			(weighted by base	sampled,	students		rates (percent)			of students
School type and jurisdiction rounded		enrollment)			weight only)	rounded	excluded		after makeups			accommodated
Wisconsin	130		100.00	100.00		3,100		0.82		88.02	12.48
Wyoming	70		100.00	100.00		2,200		1.68		87.19	12.90
Trial Urban (TUDA) Districts
Albuquerque	30		100.00	100.00		1,100		1.10		86.92	14.47
Atlanta	30		100.00	100.00		1,000		2.75		90.57	17.20
Austin	20		100.00	100.00		1,100		2.02		86.68	24.02
Baltimore City	50		100.00	100.00		1,000		2.85		90.61	21.72
Boston	50		100.00	100.00		1,000		5.72		87.12	17.28
Charlotte-Mecklenburg	30		100.00	100.00		1,100		2.68		89.31	10.90
Chicago	70		100.00	100.00		1,600		1.51		88.67	22.36
Clark County (NV)	50		100.00	100.00		1,600		1.24		86.43	5.57
Cleveland	50		100.00	100.00		900		3.91		89.60	23.11
Dallas	40		100.00	100.00		1,100		3.12		93.27	22.83
Denver	40		92.34	98.48		1,000		2.59		88.48	13.41
Detroit	40		100.00	100.00		1,000		5.10		87.61	11.23
Duval County (FL)	40		100.00	100.00		1,100		1.77		92.24	20.80
Fort Worth	30		100.00	100.00		1,000		1.41		91.91	14.01
Guilford County (NC)	30		100.00	100.00		1,000		1.02		89.39	15.27
Hillsborough County (FL)	40		100.00	100.00		1,100		3.18		88.96	20.16
Houston	40		100.00	100.00		1,500		3.65		89.49	14.45
Jefferson County (KY)	30		100.00	100.00		1,100		1.90		91.78	16.16
Los Angeles	60		100.00	100.00		1,600		2.42		89.78	9.27
Miami	70		100.00	100.00		1,600		3.34		90.11	18.85
Milwaukee	40		100.00	100.00		1,100		1.22		83.36	25.27
New York City	70		96.75	95.00		1,600		1.12		84.41	25.99
Philadelphia	40		91.14	98.36		1,000		5.13		88.26	19.72
San Diego	40		100.00	100.00		1,000		2.26		88.48	9.35
Shelby County (TN)	40		100.00	100.00		1,100		2.63		89.30	9.79

		School participation
Number of		rates (percent) before	School participation
schools in		substitution	rates (percent)		Number of		Weighted			Weighted student
original		(weighted by base	before substitution		students		percent of			participation		Weighted percent
sample,		weight and	(weighted by base		sampled,		students			rates (percent)		of students
School type and jurisdiction rounded		enrollment)	weight only)		rounded		excluded			after makeups		accommodated
District of Columbia (DCPS)	30	100.00		100.00		1,000		4.32	83.17		26.65
National private	380	35.49		32.62		1,600		0.14	94.86		5.36
Catholic	110	60.98		65.94		1,000		0.00	95.42		7.43
Non-Catholic	270	19.80		20.04		600		0.22	93.72		4.07
Other jurisdictions
DoDEA²	60	94.14		86.27		2,100		1.78	89.68		12.42

¹1¹^Includes^national^public^and^national^private^schools^locatedⁱⁿ^the^United^States^and^all^Department^of^Defense^Education^Activity^schools.

²2²Department of Defense Education Activity schools.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_grade_8_reading_for_the_2022_assessment.aspx

Shape339

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 U.S. History

The following table displays the school- and student-level response, exclusion, and accommodation rates for the grade 8 U.S history assessment. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.

The participation rates reflect the participation of the original sample schools only and do not reflect any effect of substitution. The rates weighted by the base weight and enrollment show the approximate proportion of the student population in the school type and geographic region that is represented by the responding schools in the sample. The rates weighted by just the base weight show the proportion of the school population that is represented by the responding schools in the sample. These rates differ because schools differ in size.

Participation, exclusion, and accommodation rates, grade 8 U.S. history national assessment, by school type and geographic region: 2022

School type and geographic region	Number of schools in original sample, rounded	School participation rates (percent) before substitution (weighted by base weight and enrollment)	School participation rates (percent) before substitution (weighted by base weight only)	Number of students sampled, rounded	Weighted percent of students excluded	Weighted student participation rates (percent) after makeups	Weighted percent of students accommodated
All	570	86.62	69.97	9,600	1.66	89.73	12.98
National all¹	570	86.62	69.97	9,600	1.66	89.73	12.98
Northeast all	90	82.11	60.26	1,300	1.75	88.70	16.95
Midwest all	110	87.34	71.53	1,900	1.20	90.95	11.47
South all	230	91.46	73.39	4,300	1.80	89.71	15.50
West all	140	80.38	69.74	2,200	1.76	89.20	7.50
National public	400	91.00	91.88	9,000	1.80	89.58	13.80
National private	170	33.59	33.24	600	0.00	93.57	3.40
Catholic	40	61.74	74.36	400	0.00	94.26	5.65
Non-Catholic	130	15.03	17.71	200	0.00	91.51	1.92
¹1¹^Includes^national^public,^national^private,^and^Department^of^Defense^Education^Activity^schools^locatedⁱⁿ^the^United^States.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/participation_exclusion_and_accommodation_rates_for_grade_8_u_s_history_for_the_2022_assessment.aspx

Shape344

NAEP Technical Documentation Nonresponse Bias Analyses

NCES statistical standards call for a nonresponse bias analysis for NAEP when response rates at the school or student level fall below 85 percent. To meet this requirement, separate nonresponse bias analysis (NRBA) reports were written in 2022 for each of the following NAEP samples: mathematics and reading at grades 4 and 8, civics and U.S. history at grade 8, mathematics and reading at age 9, and mathematics and reading at age 13. In addition to these reports, due to special interest in Catholic schools, a separate NRBA was conducted for this subgroup for the mathematics and reading sample at grades 4 and 8.

For the 2022 mathematics and reading assessments at grades 4 and 8, school-level response rates for private schools fell below the 85 percent threshold at both grades, while the response rates for all public school domains were above 85 percent at both grades. At the student level, response rates at grade 8 fell below 85 percent for at least one subject for the following state domains: Alaska, District of Columbia, Hawaii, New Hampshire, and New York; and the following TUDA domains: District of Columbia Public Schools, New York City, and Milwaukee. However, at grade 4, response rates for all domains were above 85 percent.

For the 2022 civics and U.S. history assessments at grade 8, response rates for private schools fell below the 85 percent threshold. At the student level, response rates for all reporting groups in this sample were above 85 percent. Similarly, for the 2022 mathematics and reading assessments at ages 9 and 13, only response rates for private schools

fell below 85 percent. Response rates for students across all reporting groups in these samples exceeded the 85 percent threshold.

The procedures and results from these analyses are summarized briefly below. The analyses conducted consider only certain characteristics of schools and students. They do not directly consider the effects of the nonresponse on student achievement, the primary focus of NAEP. Thus, these analyses cannot be conclusive of either the existence or absence of nonresponse bias for student achievement. For more details on these analyses, please see the full reports listed below:

NAEP 2022 NRBA Report for Math and Reading at Grades 4 and 8 NAEP 2022 NRBA Report for Civics and U.S. History at Grade 8 NAEP 2022 NRBA Report for LTT at Age 9

NAEP 2022 NRBA Report for LTT at Age 13

NAEP 2022 NRBA Report for Math and Reading at Grades 4 and 8 for Catholic Schools

School-level Nonresponse Bias Analyses

Each school-level analysis is typically conducted in three parts. The first part of the analysis looks for potential nonresponse bias that was introduced through school nonresponse. The second part examines the remaining potential for nonresponse bias after accounting for the effects of substitution. The third part examines the remaining potential for nonresponse bias after accounting for the effects of both school substitution and school-level nonresponse weight adjustments. The characteristics examined were census region, private school reporting group (Catholic/non-Catholic), urban-centric locale, school grade size category, and race/ethnicity percentages. In addition, two measures of the mean size of enrollment in the respective grades were considered: one is the mean grade enrollment size, i.e., mean size of school attended by an average student, which is estimated using the enrollment-size-adjusted school weight; and the other is mean-estimated grade enrollment, which is estimated using the school weight without the enrollment size adjustment. For each of the three samples, the NRBA results are summarized below.

Mathematics and Reading for Private Schools at Grades 4 and 8

NRBA showed that substitution and nonresponse adjustments decreased the number of variables with significant differences. As with prior years, nonresponse adjustments decreased nonresponse bias in each sample, because the key variable "private school reporting group" in each sample became non-significant after substitution and nonresponse adjustments. The biases of other variables, however, were still significant, or newly significant, after nonresponse adjustments.

For grade 4, the results for census region and mean grade enrollment averaged across students remained significant after substitution and nonresponse adjustments.

For grade 8, the results for census region, school size class, mean grade enrollment averaged across students, and percent Black (non-Hispanic) still have significant bias after nonresponse adjustments.

These results suggest that, even after making nonresponse adjustments, there is possibly significant nonresponse bias in the NAEP achievement results for private schools because non-trivial statistically significant differences remain between the responding and original samples for census region and mean grade enrollment averaged across students for grades 4 and 8, and for school size class and percentage Black (non-Hispanic) for grade 8. Compared with the 2019 NAEP assessment, private school response rates for NAEP 2022 were approximately 14 to 15 percentage points lower for each grade.

Civics and U.S. History at Grade 8

NRBA demonstrated that in private schools, substitution had little effect on reducing nonresponse bias. In contrast, as a result of the nonresponse adjustments, both Catholic and non-Catholic schools no longer showed nonresponse bias. Still, a significant bias remained for school size and mean grade enrollment. These two remaining biases may be explained by the following. School size is not one of the variables used to adjust for school nonresponse; thus, using the nonresponse adjusted weights would not help reduce bias for school size. The increase in bias for mean grade enrollment averaged across students could be because nonresponse adjustments had removed substantial bias from other groups, such as Catholic/Non-Catholic, which limited the ability to fully adjust for other school characteristics.

These results suggest that, even after nonresponse adjustments, there is possibly significant nonresponse bias in the NAEP achievement results for private schools because non- trivial statistically significant differences remain between the responding and original samples for school size and mean grade enrollment averaged across students.

Mathematics and Reading at Ages 9 and 13

As expected, because very few substitute schools participated at either age, substitution had little effect on reducing nonresponse bias for private schools. Nonresponse adjustments were more effective: for both ages, after adjustments the number of characteristics with significant biases was decreased and the significant bias for Catholics and non-Catholics was removed. For age 9 however, the nonresponse adjustments did not eliminate significant bias across all characteristics of the sample: though the bias decreased for the Midwest and South census regions, the bias increased for the Northeast and West regions and remained significant for the census region overall. For age 13, the nonresponse adjustments eliminated significant bias across the characteristics that had exhibited bias after substitution, but significant bias was introduced for mean enrollment averaged across students. Private school samples are small, which could explain these increases for both ages. The bias may also be due to nonresponse adjustments making some important variables less biased, with the trade-off being an increase in bias for other variables.

These results suggest that, even after nonresponse adjustments, there is possibly significant nonresponse bias in the NAEP achievement results for private schools because non- trivial statistically significant differences remain between the responding and original samples for census region at age 9 and mean enrollment averaged across students at age 13.

Mathematics and Reading at Grades 4 and 8 for Catholic Schools

For grade 4 Catholic schools, nonresponse adjustment and substitution reduced the absolute bias for census region to 0 percent since census region is explicitly used to form nonresponse adjustment cells. Based on the results of the nonresponse bias analysis, there is no evidence that the responding Catholic school sample is biased from the original eligible Catholic school sample. For grade 8 Catholic schools, after nonresponse adjustment and substitution, the absolute bias for percent Black increased. Because the nonresponse adjustments removed substantial bias from other groups, including the census region, the ability to fully adjust for other school characteristics was very limited. After the nonresponse adjustment and the substitution, a new significant characteristic, school class size was introduced. As school size is not one of the variables used in the nonresponse weighting adjustment, use of the nonresponse adjusted weights may not reduce bias for school size categories.

These results suggest that, even after nonresponse adjustments, there is possibly significant nonresponse bias in the NAEP achievement results for Catholic schools because non-trivial statistically significant differences remain between the responding and original samples for school size class and percentage Black (Non-Hispanic) for grade 8.

Student-level Nonresponse Bias Analyses

For the 2022 mathematics and reading assessments at grades 4 and 8, at the student-level, response rates fell below the critical 85 percent threshold for fourteen reporting domain and subject combinations at grade 8: New York, New York City TUDA, Alaska, District of Columbia, District of Columbia Public Schools (TUDA), and Milwaukee TUDA in both mathematics and reading; Hawaii in reading only; and New Hampshire in mathematics only. After student nonresponse adjustments, there is no evidence of substantial bias in these jurisdictions as a result of student nonresponse.

Each student-level analysis was conducted in two parts. The first part of the analysis examined the potential for nonresponse bias that was introduced through student nonresponse. The second part examined the potential for bias after accounting for the effects of nonresponse weighting adjustments. The characteristics examined were gender, race/ethnicity, relative age, National School Lunch Program eligibility, student disability (SD) status, and English learner (EL) status.

http://nces.ed.gov/nationsreportcard/tdw/weighting/2022/nonresponse_bias_analyses_for_the_2022_assessment.aspx

Shape345

File Type	application/vnd.openxmlformats-officedocument.wordprocessingml.document
File Modified	0000-00-00
File Created	0000-00-00